Paschs axiom
I geometri är Paschs axiom ett uttalande i plan geometri , som implicit används av Euclid , som inte kan härledas från postulaten som Euclid gav dem. Dess väsentliga roll upptäcktes av Moritz Pasch 1882.
Påstående
Axiomet säger att
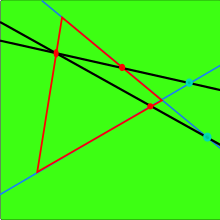
Paschs axiom — Låt A , B , C vara tre punkter som inte ligger på en linje och låt a vara en linje i planet ABC som inte möter någon av punkterna A , B , C . Om linjen a går genom en punkt i segmentet AB , går den också genom en punkt i segmentet AC , eller genom en punkt i segmentet BC .
Det faktum att segmenten AC och BC inte båda skärs av linjen a bevisas i tillägg I,1, som skrevs av P. Bernays .
En mer modern version av detta axiom är följande:
En mer modern version av Paschs axiom — I planet, om en linje skär en sida av en triangel internt så skär den exakt den andra sidan internt och den tredje sidan externt , om den inte passerar genom en vertex av triangeln.
(Om den tredje sidan är parallell med vår linje, räknar vi en "skärning i oändligheten" som extern.) En mer informell version av axiomet ses ofta:
En mer informell version av Paschs axiom - Om en linje, som inte går genom någon vertex i en triangel, möter en sida av triangeln så möter den en annan sida.
Historia
Pasch publicerade detta axiom 1882 och visade att Euklids axiom var ofullständiga. Axiomet var en del av Paschs tillvägagångssätt för att introducera begreppet ordning i plan geometri.
Ekvivalenser
I andra behandlingar av elementär geometri, med hjälp av olika uppsättningar av axiom, kan Paschs axiom bevisas som ett teorem; det är en konsekvens av planseparationsaxiomet när det tas som ett av axiomen. Hilbert använder Paschs axiom i sin axiomatiska behandling av euklidisk geometri . Med tanke på de återstående axiomen i Hilberts system kan det visas att Paschs axiom är logiskt ekvivalent med planseparationsaxiomet.
Hilberts användning av Paschs axiom
David Hilbert använder Paschs axiom i sin bok Foundations of Geometry som ger en axiomatisk grund för euklidisk geometri. Beroende på utgåvan är den numrerad antingen II.4 eller II.5. Hans uttalande ges ovan.
I Hilberts behandling förekommer detta axiom i avsnittet om ordningsaxiom och benämns ett plan för ordningsaxiom . Eftersom han inte formulerar axiomet i termer av sidorna i en triangel (som betraktas som linjer snarare än linjesegment) finns det inget behov av att tala om inre och yttre skärningar av linjen a med sidorna av triangeln ABC .
Varningar
Paschs axiom skiljer sig från Paschs teorem som är ett uttalande om ordningen av fyra punkter på en linje. Men i litteraturen finns det många fall där Paschs axiom kallas Paschs teorem. Ett anmärkningsvärt exempel på detta är Greenberg (1974, s. 67).
Paschs axiom ska inte förväxlas med Veblen-Young axiom för projektiv geometri , som kan anges som:
Veblen-Young axiom för projektiv geometri — Om en linje skär två sidor av en triangel, så skär den också den tredje sidan.
Det nämns inget om interna och externa skärningar i uttalandet av Veblen-Young axiom som endast handlar om incidensegenskapen för linjerna som möts. I projektiv geometri är begreppet betweeness (krävs för att definiera inre och yttre) inte giltigt och alla linjer möts (så problemet med parallella linjer uppstår inte).
Anteckningar
- Beutelspacher, Albrecht; Rosenbaum, Ute (1998), Projective geometry: from foundations to applications , Cambridge University Press , ISBN 978-0-521-48364-3 , MR 1629468
- Faber, Richard L. (1983), Foundations of Euclidean and Non-Euclidean Geometry , New York: Marcel Dekker, Inc., ISBN 978-0-8247-1748-3
-
Greenberg, Marvin Jay (1974), Euclidean and Non-Euclidean Geometries: Development and History (1:a upplagan), San Francisco: WH Freeman, ISBN 978-0-7167-0454-6
- Greenberg, Marvin Jay (2007), Euklidiska och Non-Euclidean Geometries: Development and History (4:e upplagan), San Francisco: WH Freeman, ISBN 978-0-7167-9948-1
-
Hilbert, David (1903), Grundlagen der Geometrie (på tyska), Leipzig: BG Teubner
- Hilbert, David (1950) [1902], The Foundations of Geometry (PDF) , översatt av Townsend, EJ, LaSalle, IL: Open Court Publishing
- Hilbert, David (1999) [1971], Foundations of Geometry , översatt av Unger, Leo (2:a upplagan), LaSalle, IL: Open Court Publishing, ISBN 978-0-87548-164-7
- Moise, Edwin (1990), Elementary Geometry from an Advanced Standpoint (tredje upplagan), Addison-Wesley, Reading, MA, sid. 74, ISBN 978-0-201-50867-3
- Pambuccian, Victor (2011), "The axiomatics of ordered geometri: I. Ordered incidence spaces.", Expositiones Mathematicae (29): 24–66, doi : 10.1016/j.exmath.2010.09.004
- Pasch, Moritz (1912) [första upplagan 1882], Vorlesungen uber neuere Geometrie (på tyska) (2:a upplagan), Leipzig: BG Teubner
-
Wylie, Jr., Clarence Raymond (1964), Foundations of Geometry , New York: McGraw-Hill, ISBN 978-0-070-72191-3
- Wylie, Jr., CR (2009) [1964], Foundations of Geometry , Mineola , New York: Dover Publications, ISBN 978-0-486-47214-0