Numerisk bländare

Den numeriska bländaren med avseende på en punkt P beror på halvvinkeln, θ ₁ , för den maximala ljuskonen som kan komma in i eller ut ur linsen och det omgivande brytningsindexet. När en ljuspenna går genom ett plant glasplan ändras dess halva vinkel till θ ₂ . På grund av Snells lag förblir den numeriska bländaren densamma: ${\text{NA}}=n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}.$

Inom optik är den numeriska bländaren ( NA ) för ett optiskt system ett dimensionslöst tal som kännetecknar intervallet av vinklar över vilka systemet kan acceptera eller avge ljus. Genom att införliva brytningsindex i sin definition har NA egenskapen att den är konstant för en stråle när den går från ett material till ett annat, förutsatt att det inte finns någon brytningskraft vid gränssnittet. Den exakta definitionen av begreppet varierar något mellan olika optikområden. Numerisk bländare används vanligtvis i mikroskopi för att beskriva acceptanskonen för ett objektiv (och därmed dess ljusinsamlingsförmåga och upplösning ), och i fiberoptik , där den beskriver intervallet av vinklar inom vilka ljus som infaller på fibern kommer att överföras längs den.

Allmän optik

Enkelt stråldiagram som visar typiska huvud- och marginalstrålar

Inom de flesta områden av optik, och särskilt inom mikroskopi , definieras den numeriska bländaren i ett optiskt system som en objektivlins av

$\mathrm {NA} =n\sin \theta ,$

där n är brytningsindexet för mediet i vilket linsen arbetar (1,00 för luft , 1,33 för rent vatten och typiskt 1,52 för immersionsolja ; se även lista över brytningsindex ), och θ är halvvinkeln för maximal ljuskägla som kan komma in i eller ur linsen. I allmänhet är detta vinkeln för den verkliga marginalstrålen i systemet. Eftersom brytningsindex är inkluderat, är NA för en penna av strålar en invariant eftersom en penna av strålar passerar från ett material till ett annat genom en plan yta. Detta visas enkelt genom att omarrangera Snells lag för att finna att n sin θ är konstant över ett gränssnitt.

I luft är linsens vinkelöppning ungefär två gånger detta värde (inom den paraxiella approximationen) . NA mäts i allmänhet med avseende på ett speciellt objekt eller bildpunkt och kommer att variera när den punkten flyttas. Inom mikroskopi hänvisar NA i allmänhet till objekt-rymd NA om inte annat anges.

I mikroskopi är NA viktigt eftersom det indikerar upplösningsförmågan hos en lins. Storleken på den finaste detalj som kan lösas (upplösningen ) är proportionell mot λ / 2NA , där λ är ljusets våglängd . Ett objektiv med en större numerisk bländare kommer att kunna visualisera finare detaljer än ett objektiv med en mindre numerisk bländare. Om man antar kvalitetsoptik ( diffraktionsbegränsad ) samlar linser med större numeriska bländare in mer ljus och ger i allmänhet en ljusare bild, men ger ett mindre skärpedjup .

Numerisk bländare används för att definiera "gropstorleken" i optiska skivformat .

Att öka förstoringen och den numeriska bländaren på objektivet minskar arbetsavståndet, dvs avståndet mellan frontlinsen och provet.

Numerisk bländare kontra f-nummer

Numerisk bländare för en tunn lins

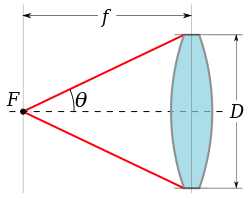
Numerisk bländare används vanligtvis inte vid fotografering . Istället uttrycks vinkelöppningen för en lins (eller en bildspegel) av f-talet , skrivet f / N , där N är f-talet som ges av förhållandet mellan brännvidden f och diametern på ingångspupillen D :

$N={\frac {f}{D}}.$

Detta förhållande är relaterat till den numeriska bländaren för bildrymden när objektivet är fokuserat på oändligt. Baserat på diagrammet till höger är linsens numeriska bländare för bildrymd:

${\text{NA}}_{\text{i}}=n\sin \theta =n\sin \left[\arctan \left({\frac {D}{2f}}\right)\right]\approx n{\frac {D}{2f}},$

sålunda N ≈ 1 / 2NAi _n , under antagande av normal användning i luft ( = 1 ).

Approximationen gäller när den numeriska bländaren är liten, men det visar sig att för väl korrigerade optiska system som kameralinser visar en mer detaljerad analys att N är nästan exakt lika med 1 / 2NA i även _vid stora numeriska bländare. Som Rudolf Kingslake förklarar, "Det är ett vanligt fel att anta att förhållandet [ D / 2f Tangenten ] faktiskt är lika med tan θ , och inte sin θ ... skulle naturligtvis vara korrekt om huvudplanen var Den fullständiga teorin om Abbes sinustillstånd visar dock att om en lins korrigeras för koma och sfärisk aberration , som alla bra fotografiska objektiv måste vara, blir det andra huvudplanet en del av en sfär med radie f centrerad kring brännpunkt". I denna mening är den traditionella tunna linsdefinitionen och illustrationen av f-nummer missvisande, och att definiera det i termer av numerisk bländare kan vara mer meningsfullt.

F -nummer som fungerar (effektivt).

F -talet beskriver linsens ljusinsamlingsförmåga i det fall där marginalstrålarna på objektsidan är parallella med linsens axel . Detta fall är vanligt förekommande inom fotografering, där objekt som fotograferas ofta är långt från kameran. När objektet inte är långt från linsen bildas bilden inte längre i linsens fokalplan och f -talet beskriver inte längre objektivets förmåga att samla ljus eller den numeriska bländaren på bildsidan. I det här fallet är den numeriska bländaren relaterad till det som ibland kallas " arbetsf - numret " eller "effektivt f -numret".

Det arbetande f -numret definieras genom att modifiera relationen ovan, med hänsyn till förstoringen från objekt till bild:

${\frac {1}{2{\text{NA}}_{\text{i}}}}=N_{\text{ w}}=\left(1-{\frac {m}{P}}\right)N,$

där N _w är det arbetande f -talet, m är linsens förstoring för ett objekt på ett visst avstånd, P är pupillförstoringen och NA definieras i termer av marginalstrålens vinkel som tidigare. Förstoringen här är vanligtvis negativ, och pupillförstoringen antas oftast vara 1 — som Allen R. Greenleaf förklarar, "Ljusstyrkan varierar omvänt som kvadraten på avståndet mellan linsens utgångspupill och plattans position eller film. Eftersom positionen för utgångspupillen vanligtvis är okänd för användaren av en lins, används istället det bakre konjugerade brännviddsavståndet; det resulterande teoretiska felet som introduceras på detta sätt är obetydligt med de flesta typer av fotografiska linser."

I fotografi skrivs faktorn ibland som 1 + m , där m representerar det absoluta värdet av förstoringen; i båda fallen är korrektionsfaktorn 1 eller högre. De två likheterna i ekvationen ovan tas var och en av olika författare som definitionen av fungerande f -tal, vilket de citerade källorna illustrerar. De är inte nödvändigtvis exakta båda två, men behandlas ofta som om de är det.

Omvänt är den numeriska bländaren på objektsidan relaterad till f -talet genom förstoringen (som tenderar till noll för ett avlägset objekt):

${\frac {1}{2{\text{NA}}_{\text{o}}}}={\frac {mP}{mP}}N.$

Laserfysik

Inom laserfysik definieras numerisk bländare något annorlunda. Laserstrålar sprids ut när de fortplantar sig, men långsamt. Långt bort från den smalaste delen av strålen är spridningen ungefär linjär med avståndet — laserstrålen bildar en ljuskon i "fjärrfältet". Relationen som används för att definiera NA för laserstrålen är densamma som den som används för ett optiskt system,

${\text{NA}}=n\sin \theta ,$

men θ definieras annorlunda. Laserstrålar har vanligtvis inte skarpa kanter som ljuskäglan som passerar genom öppningen på en lins har. Istället irradiansen gradvis bort från strålens mitt. Det är mycket vanligt att balken har en gaussisk profil. Laserfysiker väljer vanligtvis att göra θ till strålens divergens: fjärrfältsvinkeln mellan strålens axel och avståndet från axeln där irradiansen sjunker till e ⁻² gånger irradiansen på axeln. NA för en Gaussisk laserstråle relateras sedan till dess minsta punktstorlek ("strålemidja") med

${\text{NA}}\simeq {\frac {\lambda _{0}}{\pi w_{0}}},$

där λ ₀ är ljusets vakuumvåglängd och 2 w ₀ är strålens diameter på dess smalaste plats, mätt mellan e ⁻² irradianspunkter ("Full width at e ⁻² maximum of the intensity"). Detta innebär att en laserstråle som är fokuserad på en liten fläck sprids ut snabbt när den rör sig bort från fokus, medan en laserstråle med stor diameter kan hålla sig ungefär lika stor över en mycket lång sträcka. Se även: Gaussisk strålbredd .

Fiberoptik

En multimodsfiber med index n ₁ med beklädnad av index n ₂ .

En optisk fiber med flera lägen sprider endast ljus som kommer in i fibern inom ett visst intervall av vinklar, känd som fiberns acceptanskon . Halvvinkeln för denna kon kallas acceptansvinkeln , θ _max . För stegindex multimodfiber i ett givet medium, bestäms acceptansvinkeln endast av brytningsindexen för kärnan, beklädnaden och mediet:

$n\sin \theta _{\max }={\sqrt {n_{\text{core}}^{2}-n_{\text{ klädd}}^{2}}},$

där n är brytningsindex för mediet runt fibern, n _kärna är brytningsindex för fiberkärnan, och n _beklädnad är brytningsindex för beklädnaden . Medan kärnan kommer att acceptera ljus i högre vinklar, kommer dessa strålar inte helt att reflektera från gränssnittet mellan kärnan och beklädnaden och kommer därför inte att överföras till den andra änden av fibern. Härledningen av denna formel ges nedan.

När en ljusstråle faller in från ett medium med brytningsindex n till kärnan av index n _kärna vid maximal acceptansvinkel, ger Snells lag vid gränssnittet mellan kärna

$n\sin \theta _{\max }=n_{\text{core}}\sin \theta _{r}.\$

Från geometrin i ovanstående figur har vi:

$\sin \theta _{r}=\sin \left({90^{\circ }}-\theta _{c }\right)=\cos \theta _{c}$

var

$\theta _{c}=\arcsin {\frac {n_{\text{clad}}}{n_{\text{core}}}}$

är den kritiska vinkeln för total inre reflektion .

Genom att ersätta cos θ _c för sin θ _r i Snells lag får vi:

${\frac {n}{n_{\text{core}}}}\sin \theta _{\max }=\cos \theta _{c}.$

Genom att kvadrera båda sidor

${\frac {n^{2}}{n_{\text{core}}^{2}}}\sin ^{2}\theta _{\max }=\cos ^{2}\theta _{c}=1-\sin ^{2}\theta _{c}=1-{\frac {n_{\text{klädd}}^{2}}{n_{\text{kärna}}^{ 2}}}.$

När vi löser finner vi formeln ovan:

$n\sin \theta _{\max }={\sqrt {n_{\text{core}}^{2}-n_{\text{ klädd}}^{2}}},$

Denna har samma form som den numeriska aperturen (NA) i andra optiska system, så det har blivit vanligt att definiera NA för vilken typ av fiber som helst.

$\mathrm {NA} ={\sqrt {n_{\text{core}}^{2}-n_{\text{clad}}^{2}} },$

där n _kärna är brytningsindex längs fiberns centrala axel. Observera att när denna definition används blir kopplingen mellan NA och fiberns acceptansvinkel endast en approximation. Speciellt citerar tillverkare ofta "NA" för singelmodsfiber baserat på denna formel, även om acceptansvinkeln för singelmodsfiber är helt annorlunda och inte kan bestämmas enbart från brytningsindexen.

Antalet bundna moder , modvolymen , är relaterat till den normaliserade frekvensen och därmed till NA.

I multimodfibrer används ibland termen numerisk jämviktsöppning . Detta hänvisar till den numeriska aperturen med avseende på den extrema utgångsvinkeln för en stråle som kommer ut från en fiber i vilken jämviktsmodsfördelning har etablerats.

Se även

• f -nummer
• Starta numerisk bländare
• Guidad stråle , optisk fiberkontext
• Acceptansvinkel (solkoncentrator) , ytterligare sammanhang

• Den här artikeln innehåller material från allmän egendom från Federal Standard 1037C . General Services Administration . (till stöd för MIL-STD-188) .

externa länkar

• "Microscope Objectives: Numerical Aperture and Resolution" av Mortimer Abramowitz och Michael W. Davidson, Molecular Expressions: Optical Microscopy Primer (webbplats), Florida State University , 22 april 2004.
• "Basic Concepts and Formulas in Microscopy: Numerical Aperture" av Michael W. Davidson, Nikon MicroscopyU (webbplats).
• "Numerical aperture" , Encyclopedia of Laser Physics and Technology (webbplats).
• "Numerical Aperture and Resolution" , UCLA Brain Research Institute Microscopy Core Facilities (webbplats), 2007.