Nettokraft

Inom mekanik är nettokraften vektorsumman av krafter som verkar på en partikel eller ett föremål . Nettokraften är en enda kraft som ersätter effekten av de ursprungliga krafterna på partikelns rörelse . Det ger partikeln samma acceleration som alla de faktiska krafterna tillsammans som beskrivs av Newtons andra rörelselag .

Det är möjligt att bestämma vridmomentet som är förknippat med anbringningspunkten för en nettokraft så att den upprätthåller rörelsen av föremålets strålar under det ursprungliga kraftsystemet. Dess associerade vridmoment, nettokraften, blir den resulterande kraften och har samma effekt på föremålets rotationsrörelse som alla faktiska krafter tillsammans . Det är möjligt för ett kraftsystem att definiera en vridmomentfri resulterande kraft. I det här fallet har nettokraften, när den appliceras vid rätt verkningslinje , samma effekt på kroppen som alla krafter vid deras appliceringspunkter. Det är inte alltid möjligt att hitta en vridmomentfri resulterande kraft.

Total kraft

En schematisk metod för att addera krafter.

Kraft är en vektorkvantitet , vilket betyder att den har en storlek och en riktning, och den betecknas vanligtvis med fetstil som F eller genom att använda en pil över symbolen, till exempel $\scriptstyle {\vec {F }}$ .

Grafiskt representeras en kraft som ett linjesegment från dess appliceringspunkt A till en punkt B , som definierar dess riktning och storlek. Längden på segmentet AB representerar storleken på kraften.

Vektorkalkyl utvecklades i slutet av 1800-talet och början av 1900-talet. Den parallellogramregel som används för att lägga till krafter är dock från antiken och noteras uttryckligen av Galileo och Newton.

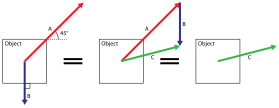
Diagrammet visar tillägget av krafterna $\scriptstyle {\vec {F}}_{1}$ och $\scriptstyle {\vec {F}}_{2}$ . Summan $\scriptstyle {\vec {F}}$ av de två krafterna ritas som diagonalen för ett parallellogram som definieras av de två krafterna.

Krafter som appliceras på en förlängd kropp kan ha olika tillämpningspunkter. Krafter är bundna vektorer och kan bara läggas till om de appliceras på samma punkt. Den nettokraft som erhålls från alla krafter som verkar på en kropp bibehåller inte dess rörelse om den inte appliceras på samma punkt och med det lämpliga vridmomentet associerat med den nya anbringningspunkten fastställt. Nettokraften på en kropp som appliceras på en enda punkt med lämpligt vridmoment är känd som den resulterande kraften och vridmomentet.

Parallelogramregel för tillägg av krafter

En kraft är känd som en bunden vektor - vilket betyder att den har en riktning och storlek och en appliceringspunkt. Ett bekvämt sätt att definiera en kraft är genom ett linjesegment från en punkt A till en punkt B . Om vi betecknar koordinaterna för dessa punkter som A = (A _x , A _y , A _z ) och B = (B _x , B _y , B _{z ), så} ges kraftvektorn som appliceras vid A av

\mathbf {F} =\mathbf {B} -\mathbf {A} =(B_{x}-A_{x},B_{y}-A_{y},B_{z}-A_{z }).

Längden på vektorn B - A definierar storleken på F och ges av

|\mathbf {F} |={\sqrt {(B_{x}-A_{x})^{2}+(B_{y}-A_{y})^{2}+(B_{ z}-A_{z})^{2}}}.

Summan av två krafter F ₁ och F ₂ applicerade vid A kan beräknas från summan av segmenten som definierar dem. Låt F ₁ = B − A och F ₂ = D − A , då är summan av dessa två vektorer

\mathbf {F} =\mathbf {F} _{1}+\mathbf {F} _{2}=\mathbf {B} -\mathbf {A} +\mathbf {D} -\mathbf {A} ,

som kan skrivas som

\mathbf {F} =\mathbf {F} _{1}+\mathbf {F} _ {2}=2({\frac {\mathbf {B} +\mathbf {D} }{2}}-\mathbf {A} )=2(\mathbf {E} -\mathbf {A} ),

där E är mittpunkten av segmentet BD som förenar punkterna B och D .

Således är summan av krafterna F ₁ och F ₂ två gånger segmentet som förenar A med mittpunkten E av segmentet som förenar ändpunkterna B och D för de två krafterna. Fördubblingen av denna längd uppnås enkelt genom att definiera ett segment BC och DC parallellt med AD respektive AB , för att fullborda parallellogrammet ABCD . Diagonalen AC för detta parallellogram är summan av de två kraftvektorerna. Detta är känt som parallellogramregeln för addition av krafter.

Översättning och rotation på grund av en kraft

Punktkrafter

När en kraft verkar på en partikel appliceras den på en enda punkt (partikelvolymen är försumbar): detta är en punktkraft och partikeln är dess appliceringspunkt. Men en yttre kraft på en utsträckt kropp (objekt) kan appliceras på ett antal av dess ingående partiklar, dvs kan "spridas" över någon volym eller yta av kroppen. För att bestämma dess rotationseffekt på kroppen kräver vi dock att vi specificerar dess appliceringspunkt (faktiskt applikationslinjen, som förklaras nedan). Problemet löses vanligtvis på följande sätt:

Ofta är volymen eller ytan som kraften verkar på relativt liten jämfört med kroppens storlek, så att den kan approximeras med en punkt. Det är vanligtvis inte svårt att avgöra om felet som orsakas av en sådan approximation är acceptabelt.
Om det inte är acceptabelt (uppenbarligen t.ex. när det gäller gravitationskraft), bör sådan "volym/yta"-kraft beskrivas som ett system av krafter (komponenter), som var och en verkar på en enda partikel, och sedan bör beräkningen göras för var och en för sig. En sådan beräkning förenklas typiskt genom användning av differentialelement i kroppsvolymen/ytan och integralkalkylen. I ett antal fall kan det dock visas att ett sådant kraftsystem kan ersättas av en enda punktkraft utan den faktiska beräkningen (som i fallet med enhetlig gravitationskraft).

Analysen av den stela kroppsrörelsen börjar i alla fall med punktkraftsmodellen. Och när en kraft som verkar på en kropp visas grafiskt, ritas det orienterade linjesegmentet som representerar kraften vanligtvis för att "börja" (eller "sluta") vid appliceringspunkten.

Stela kroppar

Hur en kraft accelererar en kropp.

I exemplet som visas i diagrammet mittemot verkar en enkel kraft $\scriptstyle {\vec {F}}$ vid appliceringspunkten H på en fri stel kropp. Kroppen har massan $\scriptstyle m$ och dess massacentrum är punkten C . I den konstanta massapproximationen orsakar kraften förändringar i kroppsrörelsen som beskrivs av följande uttryck:

{\vec {a}}={{\vec {F}} \over m}

är centrum för massaccelerationen; och

{\vec {\alpha }}={{\vec {\tau }} \over I}

är kroppens vinkelacceleration .

I det andra uttrycket är $\scriptstyle {\vec {\tau }}$ vridmomentet eller kraftmomentet, medan $\scriptstyle I$ är kroppens tröghetsmoment . Ett vridmoment orsakat av en kraft $\scriptstyle {\vec {F}}$ är en vektorstorhet definierad med avseende på någon referenspunkt:

{\displaystyle {\vec {\tau }}={\vec {r}}\times {\vec {F}}} är vridmomentvektorn,

och

\ \tau =Fk

är mängden vridmoment.

Vektorn $\scriptstyle {\vec {r}}$ är positionsvektorn för kraftappliceringspunkten, och i detta exempel är den ritad från massans centrum som referenspunkt för (se diagram). Det raka linjesegmentet $\scriptstyle k$ är hävstångsarmen för kraften $\scriptstyle {\vec {F}}$ med avseende på massans centrum. Som illustrationen antyder ändras inte vridmomentet (samma hävarm) om appliceringspunkten flyttas längs linjen för appliceringen av kraften (streckad svart linje). Mer formellt följer detta av egenskaperna hos vektorprodukten och visar att rotationseffekten av kraften endast beror på positionen för dess appliceringslinje, och inte på det särskilda valet av appliceringspunkten längs den linjen.

Vridmomentvektorn är vinkelrät mot planet som definieras av kraften och vektorn ${\displaystyle \scriptstyle {\vec {r}}} ,$ och i detta exempel är den riktad mot betraktaren; vinkelaccelerationsvektorn har samma riktning. Högerregeln relaterar denna riktning till rotationen medurs eller moturs i ritningens plan .

Tröghetsmomentet $\scriptstyle I$ beräknas med avseende på axeln genom masscentrum som är parallell med vridmomentet. Om kroppen som visas i illustrationen är en homogen skiva är detta tröghetsmoment $\scriptstyle I=mr^{2}/2$ . Om skivan har massan 0,5 kg och radien 0,8 m är tröghetsmomentet 0,16 kgm ² . Om kraften är 2 N och hävarmen 0,6 m, är vridmomentet 1,2 Nm. Vid det visade ögonblicket ger kraften till skivan vinkelaccelerationen α = $τ$ /I = 7,5 rad/s ² , och till dess masscentrum ger den den linjära accelerationen a = F / m = 4 m/s ² .

Resulterande kraft

Grafisk placering av den resulterande kraften.

Resulterande kraft och vridmoment ersätter effekterna av ett kraftsystem som verkar på rörelsen hos en stel kropp. Ett intressant specialfall är ett vridmomentfritt resultat, som kan hittas enligt följande:

Vektortillägg används för att hitta nettokraften;
Använd ekvationen för att bestämma appliceringspunkten med noll vridmoment:

{\vec {r}}\times {\vec {F}}_{\mathrm {R} }=\ summa _{i=1}^{N}({\vec {r}}_{i}\times {\vec {F}}_{i})

där ${\vec {F}}_{\mathrm {R} }$ är nettokraften, ${\vec {r}}$ lokaliserar dess appliceringspunkt, och individuella krafter är ${\vec {F}}_{i}$ med applikationspunkter ${\vec {r}}_{i}$ . Det kan vara så att det inte finns någon appliceringspunkt som ger ett vridmomentfritt resultat.

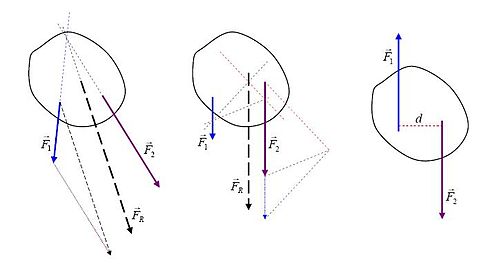
Diagrammet mittemot illustrerar enkla grafiska metoder för att hitta tillämpningslinjen för den resulterande kraften hos enkla plana system:

Tillämpningslinjerna för de faktiska krafterna ${\vec {F}}_{1}$ och ${\vec {F}}_{2}$ på bilden längst till vänster skär varandra. Efter att vektortillägg har utförts "vid platsen för ${\vec {F}}_{1}$ ", översätts den erhållna nettokraften så att dess appliceringslinje passerar genom den gemensamma skärningspunkten. Med avseende på den punkten är alla vridmoment noll, så vridmomentet för den resulterande kraften ${\vec {F}}_{\mathrm {R} }$ är lika med summan av vridmomenten för det faktiska krafter.
Illustrationen i mitten av diagrammet visar två parallella verkliga krafter. Efter vektortillägg "vid platsen för ${\vec {F}}_{2}$ ", översätts nettokraften till lämplig tillämpningslinje, där den blir den resulterande kraften $\scriptstyle {\vec {F}}_{\mathrm {R} }$ . Proceduren är baserad på sönderdelning av alla krafter till komponenter för vilka appliceringslinjerna (bleka streckade linjer) skär varandra vid en punkt (den så kallade polen, godtyckligt inställd på höger sida av illustrationen). Sedan appliceras argumenten från det föregående fallet på krafterna och deras komponenter för att visa vridmomentförhållandena.
Illustrationen längst till höger visar ett par , två lika stora men motsatta krafter för vilka nettokraften är noll, men de producerar nettovridmomentet $\scriptstyle \tau =Fd$ där $\scriptstyle \ d$ är avståndet mellan deras applikationslinjer. Eftersom det inte finns någon resulterande kraft kan detta vridmoment [beskrivs?] som "rent" vridmoment.

Användande

Vektordiagram för addition av icke-parallella krafter.

I allmänhet kan ett kraftsystem som verkar på en stel kropp alltid ersättas med en kraft plus ett rent (se föregående avsnitt) vridmoment. Kraften är nettokraften, men för att beräkna det ytterligare vridmomentet måste nettokraften tilldelas verkningslinjen. Handlingslinjen kan väljas godtyckligt, men det ytterligare rena vridmomentet beror på detta val. I ett speciellt fall är det möjligt att hitta en sådan handlingslinje att detta extra vridmoment är noll.

Den resulterande kraften och vridmomentet kan bestämmas för alla kraftkonfigurationer. Ett intressant specialfall är dock ett vridmomentfritt resultat. Detta är användbart, både konceptuellt och praktiskt, eftersom kroppen rör sig utan att rotera som om den vore en partikel.

Vissa författare skiljer inte den resulterande kraften från nettokraften och använder termerna som synonymer .

Se även