Nära uppsättningar

Figur 1. Beskrivande mycket nära mängder

I matematik är närmängder antingen rumsligt nära eller beskrivande nära. Rumsligt nära uppsättningar har icke-tom skärningspunkt . Med andra ord, rumsligt nära uppsättningar är inte disjunkta uppsättningar , eftersom de alltid har minst ett element gemensamt. Beskrivande nära uppsättningar innehåller element som har matchande beskrivningar. Sådana uppsättningar kan vara antingen osammanhängande eller icke-sammanhängande uppsättningar. Rumsligt nära uppsättningar är också beskrivande nära uppsättningar.

Figur 2. Beskrivande, minimalt nära uppsättningar

Det underliggande antagandet med beskrivande nära uppsättningar är att sådana uppsättningar innehåller element som har plats och mätbara egenskaper såsom färg och förekomstfrekvens. Beskrivningen av elementet i en uppsättning definieras av en egenskapsvektor . Jämförelse av egenskapsvektorer ger en grund för att mäta närheten av beskrivande nära uppsättningar. Nära mängdteori ger en formell grund för observation, jämförelse och klassificering av element i mängder baserat på deras närhet, antingen rumsligt eller deskriptivt. Nära uppsättningar erbjuder ett ramverk för att lösa problem baserat på mänsklig uppfattning som uppstår inom områden som bildbehandling , datorseende samt tekniska och naturvetenskapliga problem.

Nära uppsättningar har en mängd olika tillämpningar inom områden som topologi , mönsterdetektering och klassificering , abstrakt algebra , matematik inom datavetenskap och att lösa en mängd olika problem baserade på mänsklig perception som uppstår inom områden som bildanalys, bildbehandling, ansiktsigenkänning , etologi samt tekniska och naturvetenskapliga problem. Från början har beskrivande nära uppsättningar visat sig vara användbara i tillämpningar av topologi och visuell mönsterigenkänning, som spänner över ett brett spektrum av tillämpningar som inkluderar kamouflagedetektering , mikropaleontologi , handskriftsförfalskning, biomedicinsk bildanalys, innehållsbaserad bildhämtning , populationsdynamik , kvottopologi , textildesign , visuell merchandising och topologisk psykologi.

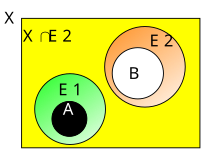
Som en illustration av graden av beskrivande närhet mellan två uppsättningar, betrakta ett exempel på Henrys färgmodell för olika grader av närhet mellan uppsättningar av bildelement i bilder (se t.ex. §4.3 ) . De två paren av ovaler i Fig. 1 och Fig. 2 innehåller färgade segment. Varje segment i figurerna motsvarar en ekvivalensklass där alla pixlar i klassen har liknande beskrivningar, dvs bildelement med liknande färger. Ovalerna i fig. 1 är närmare varandra beskrivande än ovalarna i fig. 2.

Historia

Det har observerats att det enkla begreppet närhet förenar olika begrepp av topologiska strukturer såtillvida att kategorin Nära av alla närhetsutrymmen och närhetsbevarande kartor innehåller kategorierna sTop (symmetriska topologiska utrymmen och kontinuerliga kartor), Prox ( närhetsutrymmen och $\delta$ -kartor), Unif ( likformiga rum och likformigt kontinuerliga kartor) och Cont (kontiguitetsutrymmen och angränsande kartor) som inbäddade fullständiga underkategorier. Kategorierna ${\boldsymbol {\varepsilon {ANear}}}$ och ${\boldsymbol {\varepsilon {AMer}}}$ visas som fullständiga superkategorier av olika välkända kategorier, inklusive kategorin ${\boldsymbol {sTop}}$ av symmetriska topologiska utrymmen och kontinuerliga kartor, och kategorin ${\boldsymbol {Met^{\infty }}}$ av utökade metriska utrymmen och icke-expansiva kartor. Notationen ${\boldsymbol {A}}\hookrightarrow {\boldsymbol {B}}$ läser kategori ${\boldsymbol {A}}$ är inbäddad i kategori ${\boldsymbol {B}}$ . Kategorierna ${\boldsymbol {\varepsilon AMer}}$ och ${\boldsymbol {\varepsilon ANear}}$ är superkategorier för en mängd olika bekanta kategorier som visas i Fig. 3. Låt ${\boldsymbol {\varepsilon {ANear}} }$ beteckna kategorin för alla $\varepsilon$ -närma närhetsutrymmen och sammandragningar, och låt ${\boldsymbol {\varepsilon AMer}}$ beteckna kategorin för alla $\varepsilon$ -närmar sig merotopiska mellanrum och sammandragningar.

Figur 3. Superkatter

Bland dessa välbekanta kategorier finns ${\boldsymbol {sTop}}$ , den symmetriska formen av ${\boldsymbol {Top}}$ (se kategori av topologiska utrymmen ) , kategorin med objekt som är topologiska rum och morfismer som är kontinuerliga kartor mellan dem. ${\boldsymbol {Met^{\infty }}}$ med objekt som är utökade metriska utrymmen är en underkategori till ${\boldsymbol {\varepsilon AP}}$ (har objekt $\varepsilon$ -närmar sig mellanrum och sammandragningar) (se även). Låt $\rho _{X},\rho _{Y}$ vara utökade pseudometrier på icke-tomma mängder $X,Y$ , respektive. Kartan ${\displaystyle f:(X,\rho _{X})\longrightarrow (Y,\rho _{Y})} är$ en sammandragning om och endast om ${\displaystyle f:(X,\nu _{D_{\rho _{X}}})\longrightarrow (Y,\nu _{D_{\rho _{Y}}})} är$ en kontraktion. För icke-tomma delmängder $A,B\in 2^{X}$ , avståndsfunktionen $D_{\rho }:2^{X}\times 2^{X}\longrightarrow [0,\infty ]$ definieras av

$D_{\rho }(A,B)={\begin{cases}\inf {\{\rho (a,b):a\in A,b\in B\}},&{\text {if }}A{\text{ och }}B{\text{ är inte tomma}},\\\infty ,&{\text{if }}A{\text{ eller }}B{\text{ är tomt}}.\end{cases}}$

Således är ${\boldsymbol {\varepsilon }}$ AP inbäddad som en fullständig underkategori i ${\boldsymbol {\varepsilon {ANear}}}$ av funktionatorn $F:{\boldsymbol {\varepsilon {AP}}}\longrightarrow {\boldsymbol {\varepsilon {ANear}}}$ definierad av $F((X,\rho ))=(X,\nu _{D_{\rho }})$ och $F( f)=f$ . Då $f:(X,\rho _{X})\longrightarrow (Y,\rho _{Y})$ en sammandragning om och endast om $f:(X,\nu _{D_{\rho _{X}}})\longrightarrow (Y,\nu _{D_{ \rho _{Y}}})$ är en sammandragning. Således ${\boldsymbol {\varepsilon {AP}}}$ inbäddad som en fullständig underkategori i ${\boldsymbol {\varepsilon {ANear}}}$ av funktorn $F:{\boldsymbol {\varepsilon {AP}}}\longrightarrow {\boldsymbol {\varepsilon {ANear}}}$ definierad av $F((X,\rho ))=(X,\nu _{D_{\rho }})$ och $F(f)=f.$ Sedan kategorin ${\boldsymbol {Met^{\infty }}}$ av utökade metriska utrymmen och icke-expansiva kartor är en fullständig underkategori av ${\boldsymbol {\varepsilon {AP}}}$ , därför är ${\boldsymbol {\varepsilon {ANear}}}$ också en fullständig överkategori av ${\boldsymbol {Met^{\infty }}}$ . Kategorin ${\boldsymbol {\varepsilon {ANear}}}$ är en topologisk konstruktion.

Figur 4. Frigyes Riesz , 1880-1956

Föreställningarna om nära och fjärran i matematik kan spåras tillbaka till verk av Johann Benedict Listing och Felix Hausdorff . De relaterade föreställningarna om likhet och likhet kan spåras tillbaka till JH Poincaré , som introducerade uppsättningar av liknande förnimmelser (nya toleransklasser) för att representera resultaten av GT Fechners sensationskänslighetsexperiment och ett ramverk för studiet av likhet i representativa utrymmen som modeller för vad han kallade fysisk kontinua. Elementen i ett fysiskt kontinuum (pc) är uppsättningar av förnimmelser. Begreppet en pc och olika representativa utrymmen (taktila, visuella, motoriska utrymmen) introducerades av Poincaré i en artikel från 1894 om det matematiska kontinuumet, en artikel från 1895 om rymden och geometrin och en kompendiös bok från 1902 om vetenskap och hypoteser följt av ett antal av fördjupningar, t ex ,. Artiklarna från 1893 och 1895 om continua (Pt. 1, ch. II) samt representativa rum och geometri (Pt. 2, ch IV) ingår som kapitel i. Senare introducerade F. Riesz begreppet närhet eller närhet till par uppsättningar vid International Congress of Mathematicians (ICM) 1908.

Under 1960-talet introducerade EC Zeeman toleransutrymmen för att modellera visuell perception. AB Sossinsky observerade 1986 att huvudtanken bakom toleransrymdteorin kommer från Poincaré, speciellt. År 2002 övervägde Z. Pawlak och J. Peters ett informellt förhållningssätt till uppfattningen om närhet till fysiska objekt som snöflingor som inte var begränsad till rumslig närhet. År 2006 övervägde J. Peters, A. Skowron och J. Stepaniuk ett formellt förhållningssätt till objekts beskrivande närhet i samband med närhetsutrymmen. Under 2007 introducerades beskrivande nära set av J. Peters följt av införandet av tolerans nära set. Nyligen har studiet av beskrivande nära mängder lett till algebraiska, topologiska och närliggande rymdfundament för sådana uppsättningar.

Närhet av uppsättningar

Adjektivet nära i samband med nära uppsättningar används för att beteckna det faktum att observerade särdragsvärdesskillnader för distinkta objekt är tillräckligt små för att betraktas som omöjliga att särskilja, dvs. inom en viss tolerans.

Den exakta idén om närhet eller "likhet" eller om "att vara inom tolerans" är universell nog för att dyka upp, helt naturligt, i nästan vilken matematisk miljö som helst (se t.ex. ) . Det är särskilt naturligt i matematiska tillämpningar: praktiska problem handlar oftare än inte om ungefärliga indata och kräver endast genomförbara resultat med en acceptabel felnivå.

Orden nära och fjärran används i det dagliga livet och det var ett tydligt förslag från F. Riesz att dessa intuitiva begrepp skulle göras rigorösa. Han introducerade begreppet närhet av par av uppsättningar vid ICM i Rom 1908. Detta koncept är användbart för att förenkla undervisning i kalkyl och avancerad kalkyl. Till exempel är övergången från en intuitiv definition av kontinuitet för en funktion vid en punkt till dess rigorösa epsilon-delta definition ibland svår för lärare att förklara och för elever att förstå. Intuitivt kontinuitet förklaras med hjälp av närhetsspråk, dvs en funktion $f:\mathbb {R} \rightarrow \mathbb {R}$ är kontinuerlig i en punkt $c$ , förutsatt att punkter $\{x \}$ nära $c$ gå in i punkterna $\{f(x)\}$ nära $f(c)$ . Med Riesz idé kan denna definition göras mer exakt och dess kontrapositiva är den välbekanta definitionen.

Generalisering av fast skärningspunkt

Ur en rumslig synvinkel betraktas närhet (alias närhet) som en generalisering av fast skärningspunkt . För disjunkta uppsättningar definieras en form av närhetsmängdsskärning i termer av en uppsättning objekt (extraherat från disjunkta uppsättningar) som har liknande egenskaper inom en viss tolerans (se t.ex. §3 i). Till exempel betraktas ovalarna i fig. 1 nära varandra, eftersom dessa ovaler innehåller par av klasser som uppvisar liknande (visuellt omöjliga) färger.

Efremovič närhet utrymme

Låt $X$ beteckna ett metriskt topologiskt utrymme som är försett med en eller flera närhetsrelationer och låt $2^{X}$ beteckna samlingen av alla delmängder av $X$ . Samlingen $2^{X}$ kallas kraftmängden för X $\displaystyle X}$ .

Det finns många sätt att definiera Efremovič närhet på topologiska utrymmen (diskret närhet, standard närhet, metrisk närhet, Čech närhet, Alexandroff närhet och Freudenthal närhet), För detaljer, se § 2, s. 93–94 i. Fokus här är om standardnärhet på ett topologiskt utrymme. För $B\subset X} är$ , $A$ nära $B$ (betecknas med $A\ \delta \ B$ ), förutsatt att deras stängningar har en gemensam punkt.

Stängningen av en delmängd A $\displaystyle A\in 2^{X}}$ (betecknad med ${\displaystyle {\mbox{cl}}(A)} )$ är den vanliga Kuratowski-stängningen av en uppsättning, införd i 4 §, sid. 20, definieras av

${\begin{aligned}{\mbox{cl}}(A)&=\left\{x\in X:D(x,A)=0\right\},\ {\mbox{där} }\\D(x,A)&=\inf \left\{d(x,a):a\in A\right\}.\end{aligned}}$

Dvs ${\mbox{cl}}(A)$ är mängden av alla punkter $x$ i $X$ som är nära $A$ ( $D(x,A)$ är Hausdorff-avståndet (se § 22, s. 128, in) mellan $x$ och mängden $A$ och $d(x,a)=\left|xa\right|$ (standardavstånd)). En standard närhetsrelation definieras av

$\delta =\left\{(A,B)\in 2^{X}\times 2^{X}:{\mbox{cl}}(A)\ \cap \ {\mbox{cl} }(B)\neq \emptyset \right\}.$

När set $A$ och $B$ inte har några punkter gemensamma, är uppsättningarna långt ifrån varandra (betecknas $A\ {\underline {\delta }}\ B$ ).

Följande EF-närhetsaxiom ges av Jurij Michailov Smirnov baserat på vad Vadim Arsenyevič Efremovič introducerade under första hälften av 1930-talet. Låt $A,B,E\in 2^{X}$ .

EF.1

Om uppsättningen $A$ är nära $B$ så är $B$ nära $A$ .

EF.2

$A\cup B$ är nära ${\displaystyle E} ,$ om och endast om minst en av uppsättningarna $A$ eller $B$ är nära till $E$ .

EF.3

Två punkter är nära, om och bara om, de är samma punkt.

EF.4

Alla uppsättningar är långt ifrån den tomma uppsättningen $\emptyset$ .

EF.5

För två valfria uppsättningar $A$ och $B$ som är långt ifrån varandra, finns det $C,D\in 2^{X}$ , $C\cup D=X$ , så att $A$ är långt ifrån $C$ och $B$ är långt ifrån $D$ ( Efremovič-axiom ).

Paret $(X,\delta )$ kallas ett EF- närhetsutrymme . I det här sammanhanget är ett utrymme en uppsättning med någon extra struktur. Med ett närhetsutrymme $X$ induceras strukturen av ${\displaystyle X} av EF-närhetsrelationen$$\delta$ . I ett närområde $X$ , stängningen av $A$ i $X$ sammanfaller med skärningspunkten för alla slutna uppsättningar som innehåller $A$ .

Sats 1

Stängningen av valfri mängd $A$ i närhetsutrymmet $X$ är mängden punkter $x\in X$ som är nära $A$ .

Visualisering av EF-axiom

Figur 5. Exempel på en beskrivande EF-närhetsrelation mellan mängderna $A,B$ och $C^{c}$

Låt mängden $X$ representeras av punkterna inuti det rektangulära området i fig. 5. Låt också $A,B$ vara två valfria delmängder utan skärningspunkt ( dvs. delmängder rumsligt långt från varje annat) i $X$ , som visas i Fig. 5. Låt $C^{c}=X\backslash C$ ( komplement till mängden $C$ ). Sedan från EF-axiomet, observera följande:

${\begin{aligned}A&{}\mathrel {\underline {\delta }} B,\\B&\subset C,\\D&=C^{c},\\X&=D\cup C ,\\A&\subset D,\ {\mbox{därav kan vi skriva}}\\A\ {\underline {\delta }}\ B\ &\Rightarrow \ A\ {\underline {\delta }}\ C\ {\mbox{och}}\ B\ {\underline {\delta }}\ D,\ {\mbox{för vissa}}\ C,D\ {\mbox{i}}\ X{\mbox{ så att }}C\cup D=X.\qquad \blacksquare \end{aligned}}$

Beskrivande närhetsutrymme

Beskrivande nära uppsättningar introducerades som ett sätt att lösa klassificerings- och mönsterigenkänningsproblem som härrör från disjunkta uppsättningar som liknar varandra. Nyligen har sambanden mellan nära uppsättningar i EF-utrymmen och nära uppsättningar i beskrivande EF-närhetsrum utforskats i.

Återigen, låt $X$ vara ett metriskt topologiskt utrymme och låt $\Phi =\left\{\phi _{1},\dots ,\phi _ {n}\right\}$ en uppsättning sondfunktioner som representerar egenskaper för varje $x\in X$ . Antagandet som görs här är $X$ innehåller icke-abstrakta punkter som har mätbara egenskaper som gradientorientering. En icke-abstrakt punkt har en plats och egenskaper som kan mätas (se § 3 i ).

En sondfunktion $\phi :X\rightarrow \mathbb {R}$ representerar en egenskap hos en provpunkt i $X$ . Mappningen $\Phi :X\longrightarrow \mathbb {R} ^{n}$ definieras av ${\displaystyle \Phi (x)=(\phi _{1}(x),\dots ,\phi _{n}(x))} , där$ R $\displaystyle \mathbb {R} ^{ n}}$ är ett n-dimensionellt verkligt euklidiskt vektorrum . $\Phi (x)$ är en egenskapsvektor för $x$ , som ger en beskrivning av $x\in X$ . Detta leder till exempel till en proximal vy av uppsättningar av bildpunkter i digitala bilder.

För att erhålla en beskrivande närhetsrelation (betecknad med $\delta _{\Phi }$ ) väljer man först en uppsättning sondfunktioner. Låt ${\displaystyle {\mathcal {Q}}:2^{X}\longrightarrow 2^{R^{n}}} vara en$ mappning på en delmängd av $2 ^{X}$ till en delmängd av $2^{R^{n}}$ . Låt till exempel $A,B\in 2^{X}$ och ${\mathcal {Q}}(A),{\mathcal {Q}}(B)$ betecknar uppsättningar av beskrivningar av punkter i $A,B$ . Det är,

${\begin{aligned}{\mathcal {Q}}(A)&=\left\{\Phi (a):a\in A\right\},\\{\mathcal {Q}}( B)&=\left\{\Phi (b):b\in B\right\}.\end{aligned}}$

Uttrycket $A\mathrel {\delta _{\Phi }} B$ läser $A$ är beskrivande nära $B$ . På liknande sätt läser $A\mathrel {{\underline {\delta }}_{\Phi }} B$$A$ är beskrivande långt ifrån $B$ . Den beskrivande närheten av $A$ och $B$ definieras av

$A\mathrel {\delta _{\Phi }} B\Leftrightarrow {\mathcal {Q}}({\mbox{cl}}(A))\mathrel {\delta } {\mathcal {Q}} ({\mbox{cl}}(B))\neq \emptyset .$

Den beskrivande skärningspunkten $\mathop {\cap } _{\Phi }$ mellan $A$ och $B$ definieras av

$A\mathbin {\mathop {\cap } _{\Phi }} B=\left\{x\in A\cup B:{\mathcal {Q}}(A)\mathrel {\delta } { \mathcal {Q}}(B)\right\}.$

Det vill säga, $x\in A\cup B$ är i ${\displaystyle A\mathbin {\mathop {\cap } _{\Phi }} B} ,$ förutsatt $\Phi (x)=\Phi (a)=\Phi (b)$ för vissa $a\in A, b\in B$ . Observera att $A$ och $B$ kan vara disjunkta och ändå kan $A\mathbin {\mathop {\cap } _{\Phi }} B$ vara tom.

Den beskrivande närhetsrelationen $\delta _{\Phi }$ definieras av

$\delta _{\Phi}=\left\{(A,B)\in 2^{X}\times 2^{X}:{\mbox{cl}}(A)\mathbin {\mathop {\cap } _{\Phi }} {\mbox{cl}}(B)\neq \emptyset \right\}.$

När set $A$ och $B$ inte har några punkter med matchande beskrivningar, är uppsättningarna beskrivande långt ifrån varandra (betecknas med $A\ {\underline {\delta } }_{\Phi }\ B$ ).

Den binära relationen $\delta _{\Phi }$ är en beskrivande EF-närhet , förutsatt att följande axiom är uppfyllda för $A,B,E\subset X$ .

dEF.1

Om mängden $A$ är beskrivande nära $B$ , då är $B$ beskrivande nära $A$ .

dEF.2

$A\cup B$ är beskrivande nära ${\displaystyle E} ,$ om och endast om minst en av uppsättningarna $A$ eller $B$ är beskrivande nära $E$ .

dEF.3

Två punkter $x,y\in X$ är beskrivande nära, om och bara om, beskrivningen av $x$ matchar beskrivningen av $y$ .

dEF.4

Alla icke-tomma uppsättningar är beskrivande långt från den tomma uppsättningen $\emptyset$ .

dEF.5

För valfri två uppsättningar $A$ och $B$ som är beskrivande långt ifrån varandra, det finns ${\displaystyle C,D\in 2^{X}} ,$ C $\displaystyle C\cup D=X}$ , så att $A$ är beskrivande långt ifrån $C$ och $B$ är beskrivande långt ifrån $D$ ( Descriptive Efremovič axiom ) .

Paret $(X,\delta _{\Phi })$ kallas ett beskrivande närhetsutrymme.

Proximala relationsutrymmen

En relator är en icke-tom familj av relationer ${\mathcal {R}}$ på en icke-tom uppsättning $X$ . Paret $(X,{\mathcal {R}})$ (även betecknat ${\displaystyle X({\mathcal {R}})} )$ kallas ett relatorutrymme. Relatorrum är naturliga generaliseringar av ordnade mängder och enhetliga rum. Med introduktionen av en familj av närhetsrelationer ${\mathcal {R}}_{\delta }$ på $X$ får vi ett proximalt relationsutrymme $(X,{\mathcal {R}}_ {\delta })$ . För enkelhetens skull betraktar vi endast två närhetsrelationer, nämligen Efremovič-närheten $\delta$ och den beskrivande närheten $\delta _{\Phi }$ för att definiera den deskriptiva relationen ${\mathcal {R}}_{\delta _{\Phi }}$ . Paret $(X,{\mathcal {R}}_{\delta _{\Phi }})$ kallas ett proximalt relatorutrymme . I detta arbete $X$ ett metriskt topologiskt utrymme som är försett med relationerna i en proximal relation. Med introduktionen av $(X,{\mathcal {R}}_{\delta _{\Phi }})$ , kan den traditionella stängningen av en delmängd (t.ex. ) jämföras med den nyare beskrivande stängningen av en delmängd.

I ett proximalt relatorutrymme $X$ , den beskrivande stängningen av en uppsättning $A$ (betecknad med ${\mbox{cl}}_{\Phi }(A)$ ) definieras av

${\mbox{cl}}_{\Phi}(A)=\left\{x\in X:{\Phi (x)}\mathrel {\delta} {\mathcal {Q}}({ \mbox{cl}}(A))\right\}.$

Det vill säga, $x\in X$ är i den beskrivande stängningen av $A$ , förutsatt att stängningen av $\Phi (x)$ och stängningen av ${\mathcal {Q}}({\mbox{cl}}(A))$ har minst ett element gemensamt.

Sats 2

Den beskrivande stängningen av valfri mängd $A$ i det beskrivande EF-närhetsutrymmet $(X,{\mathcal {R}}_{\delta _{\Phi } })$ är uppsättningen av punkter $x\in X$ som är beskrivande nära $A$ .

Sats 3

Kuratowski stängning av en mängd $A$ är en delmängd av den beskrivande slutningen av $A$ i ett beskrivande EF-närhetsutrymme.

Sats 4

Låt $(X,{\mathcal {R}}_{\delta _{\Phi }})$ vara ett proximalt relationsutrymme, $A\subset X$ . Sedan ${\mbox{cl}}(A)\subseteq {\mbox{cl}}_{\Phi }(A)$ .

Bevis

Låt ${\displaystyle \Phi (x)\in {\mathcal {Q}}(X\setminus {\mbox{cl}}(A))} så$ att $\Phi (x)=\Phi (a)$ för vissa $a\in {\mbox{cl}}A$ . Följaktligen, $\Phi (x)\in {\mathcal {Q}}({\mbox{cl}}_{\Phi }(A))$ . Därför, ${\mbox{cl}}(A)\subseteq {\mbox{cl}}_{\Phi }(A)$

I ett proximalt relatorutrymme leder EF-närhet $\delta$ till följande resultat för beskrivande närhet $\delta _{\Phi }$ .

Sats 5

Låt $(X,{\mathcal {R}}_{\delta _{\Phi }})$ vara ett proximalt relationsutrymme, ${\ displaystil A,B,C\subset X}$ . Då

$A\ \delta \ B\ {\mbox{implies}}\ A\ \delta _{\Phi }\ B$ .

1°

°

$(A\cup B)\ \delta \ C\ {\mbox{implies}}\ (A\cup B)\ \delta _{\Phi }\ C$ .

3°

${\mbox{cl}}A\ \delta \ {\mbox{cl}}B\ {\mbox{implies}}\ {\mbox{ cl}}A\ \delta _{\Phi }\ {\mbox{cl}}B$ .

Bevis

1°

$A\ \delta \ B\Leftrightarrow A\cap B\neq \emptyset$ . För $x\in A\cap B,\Phi (x)\in {\mathcal {Q}}(A)$ och $\Phi (x)\in {\mathcal {Q}}(B)$ . Följaktligen $A\ \delta _{\Phi }\ B$ .

1° ⇒ 2°

3°

${\mbox{cl}}A\ \delta \ {\mbox{cl}}B$ innebär att ${\mbox{cl}} A$ och ${\mbox{cl}}A$ har minst en punkt gemensam. Alltså 1° ⇒ 3°.

$\qquad \blacksquare$

Beskrivande 𝛿-kvarter

Figur 6. Exempel som visar $\delta$ -kvarter

I ett pseudometriskt proximalt relationsutrymme $X$ , området för en punkt $x\in X$ (betecknad med ${\displaystyle N_{x,\varepsilon }} ),$ för $\varepsilon >0$ , definieras av

$N_{x,\varepsilon }=\left\{y\in X:d(x,y)<\varepsilon \right\}.$

Det inre av en uppsättning $A$ (betecknad med ${\mbox{int}}(A)$ ) och gränsen för $A$ (betecknad med ${ \displaystyle {\mbox{bdy}}(A)}$ ) i ett proximalt relationsutrymme $X$ definieras av

${\begin{aligned}{\mbox{int}}(A)&=\left\{x\in X:N_{x,\varepsilon }\subseteq A\right\}.\\{\mbox {bdy}}(A)&={\mbox{cl}}(A)\setminus {\mbox{int}}(A).\end{aligned}}$

En uppsättning $A$ har en naturlig stark inkludering i en uppsättning $B$ associerad med $\delta$ } (betecknad med $A\ll _{\delta } B$ ), förutsatt $A\subset {\mbox{int}}(B)$ ; dvs ${\displaystyle A\mathrel {\underline {\delta }} X\setminus {\mbox{int}}(B)} ($ A $\displaystyle A}$ är långt ifrån komplementet till ${\ mbox{int}}(B)$ ). På motsvarande sätt har en mängd ${\displaystyle A} en$ beskrivande stark inkludering i en mängd $B$ associerad med $\delta _{\Phi }$ (betecknad med $A\mathrel {\mathop {\ll } _{\Phi }} B$ ), förutsatt ${\mathcal {Q}}(A)\ delmängd \ {\mathcal {Q}}({\mbox{int}}(B))$ ; dvs, $A\ {\underline {\delta }}_{\Phi }\ X\setminus {\mbox{int}}(B)$ ( ${\mathcal {Q}}(A)$ är långt ifrån komplementet till ${\mbox{int}}B$ ).

Låt $\mathop {\ll } _{\Phi }$ vara en beskrivande $\delta$ -grannskapsrelation definierad av

$\mathop {\ll } _{\Phi }=\left\{(A,B)\in 2^{X}\times 2^{X}:{\mathcal {Q}}(A)\ delmängd {\mathcal {Q}}({\mbox{int}}(B))\right\}.$

Det vill säga ${\displaystyle A\mathrel {\mathop {\ll } _{\Phi }} B} ,$ förutsatt att beskrivningen av varje $a\in A$ finns i uppsättningen av beskrivningar av punkterna $b\in {\mbox{int}}(B)$ . Observera nu att alla $A,B$ i det proximala relationsutrymmet $X$ så att $A\mathrel {{\underline {\delta }}_{\Phi }} B$ har disjunkta $\delta _{\Phi }$ -kvarter; dvs.

${\displaystyle A\mathrel {{\underline {\delta}}_{\Phi }} B\Leftrightarrow A\mathrel {\mathop {\ll } _{\Phi }} E1,B\mathrel {\mathop {\ ll } _{\Phi }} E2,\ {\mbox{för vissa}}\ E1,E2\delmängd X\ {\mbox{(Se fig. 6).}}} Sats$

6

Vilka två uppsättningar som helst som är beskrivande långt från varandra tillhör disjunkta beskrivande $\delta _{\Phi }$ -kvarter i ett beskrivande närområde $X$ .

En övervägande av stark inneslutning av en icke-tom uppsättning i en annan uppsättning leder till studiet av hit-and-miss-topologier och Wijsman-topologin.

Tolerans nära set

Låt $\varepsilon$ vara ett reellt tal större än noll. I studien av mängder som ligger proximalt nära inom en viss tolerans, utökas uppsättningen av närhetsrelationer ${\displaystyle {\mathcal {R}}_{\delta _{\Phi }}} med en$ pseudometrisk toleransnärhetsrelation (betecknas med ${\displaystyle \delta _{\Phi ,\varepsilon }} )$ definierad av

${\begin{aligned}D_{\Phi}(A,B)&=\inf \left\{d(\Phi (a),\Phi (a)):\Phi (a)\in { \mathcal {Q}}(A),\Phi (a)\in {\mathcal {Q}}(B)\right\},\\d(\Phi (a),\Phi (a))&= \mathop {\sum } _{i=1}^{n}|\phi _{i}(a)-\phi _{i}(b)|,\\\delta _{\Phi ,\varepsilon } &=\left\{(A,B)\in 2^{X}\times 2^{X}:|D({\mbox{cl}}(A),{\mbox{cl}}(B) )|<\varepsilon \right\}.\end{aligned}}$

Låt ${\mathcal {R}}_{\delta _{\Phi ,\varepsilon }}={\mathcal {R}}_{ \delta _{\Phi }}\cup \left\{\delta _{\Phi,\varepsilon }\right\}$ . Med andra ord, en icke-tom uppsättning utrustad med den proximala relatorn ${\mathcal {R}}_{\delta _{\Phi ,\varepsilon }}$ har en underliggande struktur som tillhandahålls av den proximala relatorn ${\mathcal {R}}_{\delta _{\Phi }}$ och ger en grund för studiet av tolerans nära mängder i $X$ som är nära inom en viss tolerans. Uppsättningar $A,B$ i ett beskrivande pseudometriskt proximalt relationsutrymme $(X,{\mathcal {R}}_{\delta _{\Phi ,\ varepsilon }})$ är tolerans nära mängder (dvs. $A\ \delta _{\Phi ,\varepsilon }\ B$ ), tillhandahålls

$D_{\Phi }(A,B)<\varepsilon .$

Toleransklasser och förklasser

Relationer med samma formella egenskaper som likhetsrelationer av förnimmelser som Poincaré anser kallas numera, efter Zeeman , toleransförhållanden . En tolerans $\tau$ på en mängd $O$ är en relation $\tau \subseteq O\times O$ som är reflexiv och symmetrisk. I algebra, termen toleransrelation används också i en snäv betydelse för att beteckna reflexiva och symmetriska relationer definierade på universum av algebra som också är kompatibla med operationer av en given algebra, dvs. de är generaliseringar av kongruensrelationer (se t.ex. ). Vid hänvisning till sådana relationer används termen algebraisk tolerans eller termen algebraisk toleransrelation . Transitiva toleransrelationer är ekvivalensrelationer. En mängd $O$ tillsammans med en tolerans $\tau$ kallas ett toleransutrymme (betecknas $(O,\tau)$ ). En mängd $A\subseteq O$ är en $\tau$ -förklass (eller kort förklass när $\tau$ förstås) om och endast om för någon $x,y\in A$ , $(x,y)\in \tau$ .

Familjen av alla förklasser av ett toleransutrymme ordnas naturligt efter mängdinkludering och förklasser som är maximala med avseende på mängdinkludering kallas $\tau$ -klasser eller bara klasser , när $\tau$ förstås . Familjen av alla klasser i rymden $(O,\tau )$ är särskilt intressant och betecknas med $H_{\tau }(O)$ . Familjen $H_{\tau }(O)$ är en täckning av $O$ .

Poincarés och Zeemans arbete om likhet förebådar införandet av nära mängder och forskning om likhetsrelationer , t.ex. Inom vetenskap och teknik är tolerans nära uppsättningar en praktisk tillämpning av studiet av uppsättningar som ligger nära inom en viss tolerans. En tolerans $\varepsilon \in (0,\infty ]$ är direkt relaterad till idén om närhet eller likhet ( dvs. , som ligger inom en viss tolerans) vid jämförelse av objekt. Med hjälp av Poincarés tillvägagångssätt för att definiera visuella rum och Zeemans förhållningssätt till toleransrelationer är grundidén att jämföra objekt som bildfläckar i det inre av digitala bilder.

Exempel

Enkelt exempel

Följande enkla exempel visar konstruktionen av toleransklasser från verkliga data. Betrakta de 20 objekten i tabellen nedan med $|\Phi |=1$ .

Exempel perceptuellt system

$x_{i}$	$\phi (x)$	$x_{i}$	$\phi (x)$	$x_{i}$	$\phi (x)$	$x_{i}$	$\phi (x)$
$x_{1}$	.4518	$x_{6}$	.6943	$x_{11}$	.4002	$x_{16}$	.6079
$x_{2}$	.9166	$x_{7}$	.9246	$x_{12}$	.1910	$x_{17}$	.1869
$x_{3}$	.1398	$x_{8}$	.3537	$x_{13}$	.7476	$x_{18}$	.8489
$x_{4}$	.7972	$x_{9}$	.4722	$x_{14}$	.4990	$x_{19}$	.9170
$x_{5}$	.6281	$x_{10}$	.4523	$x_{15}$	.6289	$x_{20}$	.7143

Låt ett toleransförhållande definieras som

$\cong _{\varepsilon }{}\Vänsterpil \{(x,y) \in O\times O:\;\parallel \Phi (x)-\Phi (y)\parallel _{_{2}}\leq \varepsilon \}$

Sedan, inställning av $\varepsilon =0.1$ ger följande toleransklasser:

${\begin{aligned}H_{\cong _{\varepsilon }}(O)={}&\{\{x_{1},x_{8},x_{10},x_{11}\ },\{x_{1},x_{9},x_{10},x_{11},x_{14}\},\\&\{x_{2},x_{7},x_{18} ,x_{19}\},\\&\{x_{3},x_{12},x_{17}\},\\&\{x_{4},x_{13},x_{20}\ },\{x_{4},x_{18}\},\\&\{x_{5},x_{6},x_{15},x_{16}\},\{x_{5}, x_{6},x_{15},x_{20}\},\\&\{x_{6},x_{13},x_{20}\}\}.\end{aligned}}$

Observera att varje objekt i en toleransklass uppfyller villkoret $\parallel \Phi (x)-\Phi (y)\parallel _{2}\leq \ varepsilon$ , och att nästan alla objekt förekommer i mer än en klass. Dessutom skulle det finnas tjugo klasser om ourskiljbarhetsrelationen användes eftersom det inte finns två objekt med matchande beskrivningar.

Exempel på bildbehandling

Figur 7. Exempel på bilder som ligger nära varandra. (a) och (b) Bilder från det fritt tillgängliga LeavesDataset (se t.ex. www.vision.caltech.edu/archive.html).

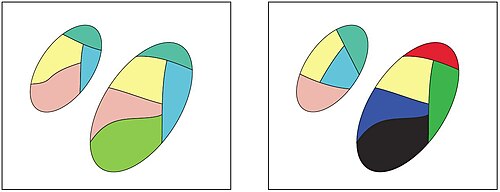
Följande exempel ger ett exempel baserat på digitala bilder. Låt en delbild definieras som en liten delmängd av pixlar som hör till en digital bild så att pixlarna som ingår i delbilden bildar en kvadrat. Låt sedan uppsättningarna $X$ respektive $Y$ representera underbilderna som erhållits från två olika bilder, och låt $O=\{X\cup Y\}$ . Låt slutligen beskrivningen av ett objekt ges av den gröna komponenten i RGB färgmodell . Nästa steg är att hitta alla toleransklasser med hjälp av toleransrelationen definierad i föregående exempel. Med hjälp av denna information kan toleransklasser bildas som innehåller objekt som har liknande (inom några små $\varepsilon$ ) värden för den gröna komponenten i RGB-färgmodellen. Dessutom bör bilder som är nära (lika) varandra ha toleransklasser uppdelade mellan båda bilderna (istället för en toleransklass som enbart finns i en av bilderna). Till exempel visar figuren som medföljer detta exempel en delmängd av toleransklasserna erhållna från två bladbilder. I denna figur är varje toleransklass tilldelad en separat färg. Som kan ses delar de två bladen liknande toleransklasser. Detta exempel belyser ett behov av att mäta graden av närhet för två uppsättningar.

Närhetsmått

Låt $(U,{\mathcal {R}}_{\delta _{\Phi ,\varepsilon }})$ beteckna ett särskilt beskrivande pseudometriskt EF-proximalt relatorutrymme utrustat med närhetsrelationen $\delta _{\Phi ,\varepsilon }$ och med icke-tomma delmängder $X,Y\in 2^{U}$ och med toleransrelationen $\cong _{\Phi ,\varepsilon }$ definierad i termer av en uppsättning sonder $\Phi$ och med $\varepsilon \in (0,\infty ]$ , var

Figur 8. Exempel på grad av närhet mellan två uppsättningar: (a) Hög grad av närhet och (b) Låg grad av närhet.

$\simeq _{\Phi ,\varepsilon }=\{(x,y)\in U\times U\mid \ |\Phi (x)-\Phi (y)|\leq \varepsilon \}.$

Antag vidare att $Z=X\cup Y$ och låt $H_{\tau _{\Phi ,\varepsilon }}(Z)$ beteckna familj av alla klasser i rymden $(Z,\simeq _{\Phi ,\varepsilon })$ .

Låt $A\subseteq X,B\subseteq Y$ . Avståndet $D_{_{tNM}}:2^{U}\times 2^{U}:\longrightarrow [0,\infty ]$ definieras av

$D_{_{tNM}}( X,Y)={\begin{cases}1-tNM(A,B),&{\mbox{if }}X{\mbox{ och }}Y{\mbox{ är inte tomma}},\\\ infty ,&{\mbox{if }}X{\mbox{ eller }}Y{\mbox{ är tomt}},\end{cases}}$

var

$tNM(A,B)={\Biggl (}\sum _{C\in H_{\tau _{\Phi,\varepsilon }}(Z)}|C|{\Biggr )}^{- 1}\cdot \sum _{C\in H_{\tau _{\Phi ,\varepsilon }}(Z)}|C|{\frac {\min(|C\cap A|,|[C\cap B|)}{\max(|C\cap A|,|C\cap B|)}}.$

Detaljerna om $tNM$ ges i. Tanken bakom $tNM$ är att uppsättningar som är lika bör ha ett liknande antal objekt i varje toleransklass. Således, för varje toleransklass som erhålls från täckningen av ${\displaystyle Z=X\cup Y} ,$ räknar $tNM$ antalet objekt som tillhör $X$ och $Y$ och tar förhållandet (som en riktig bråkdel) av deras kardinaliteter. Dessutom viktas varje förhållande med den totala storleken på toleransklassen (vilket ger betydelse för de större klasserna) och det slutliga resultatet normaliseras genom att dividera med summan av alla kardinaliteter. Intervallet för $tNM$ ligger i intervallet [0,1], där värdet 1 erhålls om mängderna är ekvivalenta (baserat på objektbeskrivningar) och värdet 0 erhålls om de inte har någon gemensamma beskrivningar.

Som ett exempel på graden av närhet mellan två uppsättningar, betrakta figuren nedan där varje bild består av två uppsättningar objekt, $X$ och $Y$ . Varje färg i figurerna motsvarar en uppsättning där alla objekt i klassen delar samma beskrivning. Tanken bakom $tNM$ är att uppsättningarnas närhet i ett perceptuellt system baseras på kardinaliteten hos toleransklasser som de delar. Således är uppsättningarna på vänster sida av figuren närmare (mer nära) varandra när det gäller deras beskrivningar än uppsättningarna på högra sidan av figuren.

Near set evaluation and recognition (NEAR) system

Figur 9. NÄRA system GUI.

Near set Evaluation and Recognition (NEAR)-systemet är ett system som utvecklats för att demonstrera praktiska tillämpningar av near set-teori på problemen med bildsegmenteringsutvärdering och bildkorrespondens. Det motiverades av ett behov av ett fritt tillgängligt mjukvaruverktyg som kan ge resultat för forskning och för att skapa intresse för nära mängdteori. Systemet implementerar ett Multiple Document Interface (MDI) där varje separat bearbetningsuppgift utförs i sin egen underordnade ram. Objekten (i den närmast angivna betydelsen) i detta system är delbilder av bilderna som bearbetas och sondfunktionerna (särdragen) är bildbehandlingsfunktioner definierade på delbilderna. Systemet skrevs i C++ och designades för att underlätta tillägget av nya bearbetningsuppgifter och probefunktioner. För närvarande utför systemet sex huvuduppgifter, nämligen att visa ekvivalens- och toleransklasser för en bild, utföra segmenteringsutvärdering, mäta närheten av två bilder, utföra Content Based Image Retrieval (CBIR) och visa utdata från bearbetning av en bild med hjälp av en specifik sondfunktion.

Närhetssystem

Figur 10. Närhetssystemet.

Proximity System är en applikation utvecklad för att demonstrera deskriptivt baserade topologiska tillvägagångssätt för närhet och närhet inom ramen för digital bildanalys. Närhetssystemet växte fram ur S. Naimpallys och J. Peters arbete om topologiska utrymmen. Proximity System är skrivet i Java och är tänkt att köras i två olika operativa miljöer, nämligen på Android-smarttelefoner och surfplattor, samt stationära plattformar som kör Java Virtual Machine. När det gäller skrivbordsmiljön är Proximity System en plattformsoberoende Java-applikation för Windows, OSX och Linux-system, som har testats på Windows 7 och Debian Linux med Sun Java 6 Runtime. När det gäller implementeringen av de teoretiska tillvägagångssätten använder både Android- och skrivbordsbaserade applikationer samma back-end-bibliotek för att utföra de beskrivningsbaserade beräkningarna, där de enda skillnaderna är användargränssnittet och Android-versionen har mindre tillgängliga funktioner pga. till begränsningar av systemresurser.

Se även

• Alternativ mängdlära
• Kategori:Matematiska relationer
• Kategori:Topologi
• Funktionsvektor
• Närhetsutrymme
• Grovt set
• Topologi

Vidare läsning

•   Naimpally, SA; Peters, JF (2013). Topologi med applikationer. Topologiska utrymmen via nära och fjärran . World Scientific Publishing. Co. Pte. Ltd. ISBN 978-981-4407-65-6 .
• Naimpally, SA; Peters, JF; Wolski, M. (2013). Nära mängdteori och tillämpningar . Matematik i datavetenskap. Vol. 7. Berlin: Springer.
• Peters, JF (2014). Digitala bilders topologi. Visuellt mönsterupptäckt i närliggande utrymmen . Referensbibliotek för intelligenta system. Vol. 63. Berlin: Springer.
• Henry, CJ; Peters, JF (2012). System för nästan uppsättning utvärdering och igenkänning (NEAR) V3.0 . UM CI Laboratory Technical Report nr TR-2009-015. Computational Intelligence Laboratory, University of Manitoba.
• Concilio, A. Di (2014). Närhet: Ett kraftfullt verktyg inom förlängningsteori, funktionsrum, hyperrymder, booleska algebror och punktfri geometri . UM CI Laboratory Technical Report nr TR-2009-021. Computational Intelligence Laboratory, University of Manitoba.
•   Peters, JF; Naimpally, SA (2012). "Applikationer av nära set" (PDF) . Meddelanden från American Mathematical Society . 59 (4): 536–542. CiteSeerX 10.1.1.371.7903 . doi : 10.1090/noti817 .