Mohr-Mascheroni-satsen

Inom matematiken säger Mohr -Mascheroni-satsen att vilken geometrisk konstruktion som helst som kan utföras av en kompass och en raksträcka kan utföras enbart av en kompass.

Det måste förstås att med "valfri geometrisk konstruktion" syftar vi på figurer som inte innehåller några räta linjer, eftersom det är helt klart omöjligt att rita en rak linje utan en rätlinje. Det är underförstått att en linje bestäms förutsatt att två distinkta punkter på den linjen ges eller konstrueras, även om ingen visuell representation av linjen kommer att finnas. Teoremet kan uttryckas mer exakt som:

Alla euklidiska konstruktioner, i den mån de givna och nödvändiga elementen är punkter (eller cirklar), kan kompletteras med enbart kompassen om den kan kompletteras med både kompassen och rätlinjen tillsammans.

Även om användningen av en rätning kan göra en konstruktion betydligt enklare, visar satsen att varje uppsättning punkter som helt definierar en konstruerad figur kan bestämmas med enbart kompass, och det enda skälet att använda en rätlina är för estetiken att se raka linjer , vilket för konstruktionsändamål är funktionellt onödigt.

Historia

Resultatet publicerades ursprungligen av Georg Mohr 1672, men hans bevis försvann i dunkel fram till 1928. Satsen upptäcktes oberoende av Lorenzo Mascheroni 1797 och den var känd som Mascheronis sats tills Mohrs verk återupptäcktes.

Flera bevis på resultatet är kända. Mascheronis bevis från 1797 baserades i allmänhet på idén att använda reflektion i en linje som det viktigaste verktyget. Mohrs lösning var annorlunda. 1890 publicerade August Adler ett bevis med inversionstransformationen .

En algebraisk metod använder isomorfismen mellan det euklidiska planet och det reella koordinatutrymmet $\mathbb {R} ^{2}$ . På så sätt bevisades en starkare version av satsen 1990. Den visar också satsens beroende av Arkimedes axiom (som inte kan formuleras på ett första ordningens språk ).

Konstruktivt bevis

Skissera

För att bevisa satsen måste var och en av de grundläggande konstruktionerna av kompass och raksträcka bevisas vara möjliga med enbart en kompass, eftersom dessa är grunden för, eller elementära steg för, alla andra konstruktioner. Dessa är:

Skapa linjen genom två befintliga punkter
Skapa cirkeln genom en punkt med centrum en annan punkt
Skapar punkten som är skärningspunkten mellan två befintliga, icke-parallella linjer
Skapa en eller två punkter i skärningspunkten mellan en linje och en cirkel (om de skär varandra)
Skapa en eller två punkter i skärningspunkten mellan två cirklar (om de skär varandra).

#1 - En linje genom två punkter

Det är underförstått att en rät linje inte kan dras utan en rätlinje. En linje anses vara given av två valfria punkter, eftersom varje sådant par definierar en unik linje. I enlighet med syftet med satsen som vi vill bevisa behöver den faktiska linjen inte dras utan av estetiska skäl.

#2 - En cirkel genom en punkt med definierat centrum

Detta kan göras enbart med en kompass. En rätlina behövs inte för detta.

#5 - Skärning av två cirklar

Denna konstruktion kan också göras direkt med en kompass.

#3, #4 - De andra konstruktionerna

För att bevisa satsen behöver alltså endast kompasskonstruktioner för #3 och #4 ges.

Notation och anmärkningar

Följande notation kommer att användas i den här artikeln. En cirkel vars centrum ligger i punkt $U$ och som passerar genom punkt $V$ kommer att betecknas med $U (V)$ . En cirkel med centrum $U och radie$ $U (r ) specificerad$ av ett tal, $r$ eller ett linjesegment $AB$ kommer att betecknas med respektive $U (AB)$ .

I allmänna konstruktioner finns det ofta flera varianter som ger samma resultat. De val som görs i en sådan variant kan göras utan förlust av allmänhet. Men när en konstruktion används för att bevisa att något kan göras är det inte nödvändigt att beskriva alla dessa olika val och för tydlighetens skull kommer endast en variant att ges nedan. Men många konstruktioner kommer i olika former beroende på om de använder cirkelinversion eller inte och dessa alternativ kommer att ges om möjligt.

Det är också viktigt att notera att några av konstruktionerna som bevisar Mohr-Mascheroni-satsen kräver godtycklig placering av punkter i rymden, som att hitta mitten av en cirkel när den inte redan tillhandahålls (se konstruktion nedan). I vissa konstruktionsparadigm - som i den geometriska definitionen av det konstruerbara talet - kan detta vara förbjudet. I ett sådant paradigm, till exempel, kommer cirklar utan deras centra inte att tillhandahållas av hypoteser, så det är ingen fråga.

Några preliminära konstruktioner

För att bevisa ovanstående konstruktioner #3 och #4, som ingår nedan, förklaras även några nödvändiga mellanliggande konstruktioner nedan eftersom de används och refereras ofta. Dessa är också kompasskonstruktioner. Alla konstruktioner nedan förlitar sig på #1, #2, #5 och alla andra konstruktioner som är listade före den.

Kompassekvivalenssats (cirkelöversättning)

Förmågan att översätta, eller kopiera, en cirkel till ett nytt centrum är avgörande i dessa bevis och grundläggande för att fastställa sanningshalten i satsen. Skapandet av en ny cirkel med samma radie som den första, men centrerad på en annan punkt, är nyckelfunktionen som skiljer den kollapsande kompassen från den moderna, stela kompassen. Med den stela kompassen är detta en trivialitet, men med den kollapsande kompassen är det en fråga om konstruktionsmöjlighet. Likvärdigheten mellan en kollapsande kompass och en stel kompass bevisades av Euclid (bok I Proposition 2 av The Elements ) med hjälp av en rak kant och kollapsande kompass när han i huvudsak konstruerar en kopia av en cirkel med ett annat centrum. Denna likvärdighet kan också fastställas med enbart kompass, ett bevis på det finns i huvudartikeln.

Att reflektera en punkt över en linje

Punktsymmetri

Givet ett linjesegment $AB$ och en punkt $C$ som inte ligger på linjen som bestäms av det segmentet, konstruera bilden av $C$ vid reflektion över denna linje.

Konstruera två cirklar: en centrerad vid $A$ och en centrerad vid $B$ , båda går genom $C$ .
D , den andra skärningspunkten för de två cirklarna, är reflektionen av C över linjen AB .
- Om $C = D$ (det vill säga det finns en unik skärningspunkt för de två cirklarna), så är $C$ sin egen reflektion och ligger på linjen $AB$ (i motsats till antagandet), och de två cirklarna är internt tangentiella.

Förlänga längden på ett linjesegment

En kompasskonstruktion för att fördubbla längden på segment AB

Givet ett linjeavsnitt $AB,$ hitta en punkt $C$ på linjen $AB$ så att $B$ är mittpunkten på linjeavsnittet $AC$ .

Konstruera punkt $D$ som skärningspunkten mellan cirklarna $A (B)$ och $B (A)$ . (∆ ABD är en liksidig triangel.)
Konstruera punkten $E \neq A$ som skärningspunkten mellan cirklarna $D (B)$ och $B (D)$ . (∆ DBE är en liksidig triangel.)
Slutligen, konstruera punkt $C \neq D$ som skärningspunkten mellan cirklarna $B (E)$ och $E (B)$ . (∆ EBC är en liksidig triangel, och de tre vinklarna vid $B$ visar att $A, B och C$ är kolinjära.)

Denna konstruktion kan upprepas så ofta som behövs för att hitta en punkt $Q$ så att längden på linjesegmentet $AQ$ = $n$ ⋅ längden av linjesegmentet $AB$ för ett positivt heltal $n$ .

Inversion i en cirkel

Punktinversion i en cirkel

Givet en cirkel $B (r)$ , för någon radie $r$ (i svart) och en punkt $D (\neq B)$ konstruera punkten $I$ som är inversen av $D$ i cirkeln. Naturligtvis finns det ingen inversion för en punkt ${\textstyle D=B}$ .

Rita en cirkel $D (B)$ (i rött).
Antag att den röda cirkeln skär den svarta cirkeln vid E och E'
- om cirklarna inte skär varandra i två punkter se nedan för en alternativ konstruktion.
- om cirklarna skär varandra i endast en punkt, $E=E'$ , är det möjligt att invertera $D$ helt enkelt genom att dubbla längden på $EB$ (fyradubbla längden av $DB$ ).
Spegla cirkelcentrum $B$ $B$ över linjen $EE'$ $EE'$ :
1. Konstruera två nya cirklar $E (B)$ och $E' (B)$ (i ljusblått).
2. De ljusblå cirklarna skär varandra vid $B$ och i en annan punkt $I \neq B$ .
Punkt $I$ är den önskade inversen av $D$ i den svarta cirkeln.

Punkt $I$ är sådan att radien $r$ för $B (r)$ är till $IB$ som $DB$ är till radien; eller $IB / r = r / DB$ .

I händelse av att ovanstående konstruktion misslyckas (det vill säga den röda cirkeln och den svarta cirkeln inte skär varandra i två punkter), hitta en punkt $Q$ på linjen $BD$ så att längden på linjesegmentet $BQ$ är en positiv heltalsmultipel, säg $n$ , av längden av $BD$ och är större än $r / 2$ (detta är möjligt med Arkimedes axiom). Hitta $Q'$ inversen av $Q$ i cirkel $B (r)$ enligt ovan (de röda och svarta cirklarna måste nu skära varandra i två punkter). Punkten $I$ erhålls nu genom att utöka $BQ'$ så att $BI$ = $n \cdot BQ'$ .

Bestämma mitten av en cirkel genom tre punkter

Enbart kompasskonstruktion av en cirkels centrum genom tre punkter (A,B,C)

Med tanke på tre icke-kollinjära punkter $A$ , $B$ och $C$ , hitta centrum $O$ i den cirkel som de bestämmer.

Konstruera punkt $D$ , inversen av $C$ i cirkeln $A (B)$ .
Reflektera $A$ på linjen $BD$ till punkten $X$ .
$O$ är inversen av $X$ i cirkeln $A (B)$ .

Skärning mellan två icke-parallella linjer (konstruktion #3)

Enbart kompasskonstruktion av skärningspunkten mellan två linjer (inte alla konstruktionssteg visas)

Givet icke-parallella linjer $AB$ och $CD$ , hitta deras skärningspunkt, $X$ .

Välj cirkel $O (r)$ med godtycklig radie vars centrum $O$ inte ligger på någon av linjerna.
Invertera punkterna $A$ och $B$ i cirkel $O (r)$ till punkterna $A'$ respektive $B'$ .
Linjen $AB$ inverteras till cirkeln som går genom $O$ , $A'$ och $B'$ . Hitta mitten $E$ i denna cirkel.
Invertera punkterna $C$ och $D$ i cirkel $O (r)$ till punkterna $C'$ respektive $D'$ .
Linjen $CD$ inverteras till cirkeln som går genom $O$ , $C'$ och $D'$ . Hitta mitten $F$ i denna cirkel.
Låt $Y \neq O$ vara skärningspunkten mellan cirklarna $E (O)$ och $F (O)$ .
$X$ är inversen av $Y$ i cirkeln $O (r)$ .

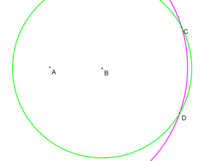
Skärningspunkten mellan en linje och en cirkel (konstruktion #4)

Enbart kompasskonstruktionen av skärningspunkterna för en linje och en cirkel delas upp i två fall beroende på om cirkelns centrum är eller inte är i linje med linjen.

Cirkelcentrum är inte i linje med linjen

Antag att cirkelns mittpunkt inte ligger på linjen.

Linje-cirkel skärning (icke-kollinjärt fall)

Givet en cirkel $C (r)$ (i svart) och en linje $AB$ . Vi vill konstruera skärningspunkterna, $P$ och $Q$ , mellan dem (om de finns).

Konstruera punkten D , som är reflektionen av punkt C över linjen AB . (Se ovan.)
- Under antagandet av detta fall, $C \neq D$ .
Konstruera en cirkel $D (r)$ (i rött). (Se ovan, kompassekvivalens.)
Skärningspunkterna mellan cirkel C ( r ) och den nya röda cirkeln D ( r ) är punkterna P och Q.
- Om de två cirklarna är (externt) tangentiella så är $P=Q$ .
Punkterna P och Q är skärningspunkterna för cirkeln C ( r ) och linjen AB .
- Om $P=Q$ så är linjen tangentiell till cirkeln $C(r)$ .

En alternativ konstruktion med cirkelinversion kan också ges.

Givet en cirkel $C (r)$ och en linje $AB$ . Vi vill konstruera skärningspunkterna, $P$ och $Q$ , mellan dem (om de finns).

Invertera punkterna A och B i cirkeln C ( r ) till punkterna A' respektive B' .
- Under antagandet av detta fall är punkterna $A'$ , $B'$ och $C$ inte kolinjära.
Hitta mitten $E$ i cirkeln som går genom punkterna $C$ , $A'$ och $B'$ .
Konstruera cirkeln $E (C)$ , som representerar inversionen av linjen $AB$ till cirkeln $C (r)$ .
P och Q är skärningspunkterna för cirklarna C ( r ) och E ( C ) .
- Om de två cirklarna är (internt) tangentiella så är $P=Q$ , och linjen är också tangentiell.

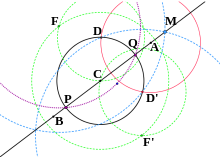
Cirkelcentrum är i linje med linjen

Enbart kompasskonstruktion av skärningspunkten mellan en cirkel och en linje (cirkel mitt på linjen)

Med tanke på cirkeln $C (D)$ vars centrum $C$ ligger på linjen $AB$ , hitta punkterna $P$ och $Q$ , skärningspunkterna för cirkeln och linjen.

Konstruera punkten $D' \neq D$ som den andra skärningspunkten mellan cirklarna $A (D)$ och $C (D)$ .
Konstruera punkt $F$ som skärningspunkten mellan cirklarna $C (DD')$ och $D (C)$ . ( $F$ är det fjärde hörnet av parallellogrammet $CD'DF$ .)
Konstruera punkten $F'$ som skärningspunkten mellan cirklarna $C (DD')$ och $D' (C)$ . ( $F'$ är det fjärde hörnet av parallellogrammet $CDD'F'$ .)
Konstruera punkten $M$ som en skärningspunkt mellan cirklarna $F (D')$ och $F' (D)$ . ( $M$ ligger på $AB$ .)
Punkterna $P$ och $Q$ är skärningspunkterna mellan cirklarna $F (CM)$ och $C (D)$ .

Sålunda har det visat sig att hela den grundläggande konstruktionen man kan utföra med en rätlina och kompass kan göras med enbart en kompass, förutsatt att man förstår att en linje inte kan ritas bokstavligen utan endast definieras av två punkter.

Andra typer av begränsad konstruktion

Renässansmatematikerna Lodovico Ferrari , Gerolamo Cardano och Niccolò Fontana Tartaglia och andra kunde på 1500-talet visa att vilken linjal-och-kompass-konstruktion som helst kunde åstadkommas med en rakled och en kompass med fast bredd (dvs. en rostig kompass) .

Motiverad av Mascheronis resultat antog Jean Victor Poncelet 1822 en variant på samma tema. Han föreslog att alla möjliga konstruktioner med rätning och kompass kunde göras med enbart rätlina. Det enda kravet är dock att en enda cirkel med dess centrum identifierat måste tillhandahållas. Detta påstående, nu känt som Poncelet-Steiner-satsen , bevisades av Jakob Steiner elva år senare.

Ett bevis som senare gavs 1904 av Francesco Severi mildrar kravet på att en hel cirkel ska tillhandahållas, och visar att varje liten båge av cirkeln, så länge som centrum fortfarande finns, fortfarande är tillräcklig.

Dessutom kan själva mitten utelämnas istället för delar av bågen, om det ersätts med något annat tillräckligt, såsom en andra koncentrisk eller skärande cirkel, eller en tredje cirkel, eller en icke-korsande andra cirkel förutsatt att en punkt på någondera centrumlinjen eller den radiella axeln mellan dem är given.

Kompassekvivalenssatsen visar att i alla de konstruktioner som nämns ovan kan den välbekanta moderna kompassen med sin fixerbara bländare, som kan användas för att överföra avstånd , ersättas med en "hopfällbar kompass", en kompass som kollapsar när den lyfts från en sida, så att den inte direkt kan användas för att överföra avstånd. Faktum är att Euklides ursprungliga konstruktioner använder en hopfällbar kompass.

Se även

Anteckningar

Eves, Howard (1963), A Survey of Geometry (volym ett) , Allyn och Bacon
Hungerbühler, Norbert (1994), "A Short Elementary Proof of the Mohr–Mascheroni Theorem", The American Mathematical Monthly , 101 (8): 784–787, doi : 10.1080/00029890.1994.11997027
Pedoe, Dan (1988) [1970], Geometry / A Comprehensive Course , Dover, ISBN 978-0-486-65812-4

Vidare läsning

Pedoe, Dan (1995) [1957], "1 Sektion 11: Compass geometri", Circles / A Mathematical View , Mathematical Association of America, s. 23–25, ISBN 978-0-88385-518-8
Posamentier, Alfred S.; Geretschläger, Robert (2016), "8. Mascheroni-konstruktioner med endast kompassen", Cirkeln , Prometheus-böcker, s. 197–216, ISBN 978-1-63388-167-9

externa länkar

Konstruktion endast med kompassen