Modulärt galler

Ett modulärt gitter av ordningen dimension 2. Som med alla finita 2-dimensionella gitter är dess Hasse-diagram en st -planär graf .

I den gren av matematiken som kallas ordningsteori är ett modulärt gitter ett gitter som uppfyller följande självdubbla villkor ,

Modulär lag: $a \leq b$ innebär $a \lor (x \land b) = (a \lor x) \land b$

där $x, a, b$ är godtyckliga element i gittret, ≤ är den partiella ordningen , och ∨ och ∧ (kallas join respektive meet ) är operationerna i gittret. Denna frasering betonar en tolkning i termer av projektion på subgitteret $[a, b]$ , ett faktum som kallas diamantisomorfismens teorem . Ett alternativt men ekvivalent villkor som anges som en ekvation (se nedan) betonar att modulära gitter bildar en variation i betydelsen universell algebra .

Modulära gitter uppstår naturligt i algebra och inom många andra områden inom matematiken. I dessa scenarier är modularitet en abstraktion av den andra isomorfismsatsen . Till exempel bildar delutrymmena i ett vektorrum (och mer generellt delmodulerna i en modul över en ring ) ett modulärt gitter.

I ett inte nödvändigtvis modulärt gitter kan det fortfarande finnas element $b$ för vilka modullagen gäller i samband med godtyckliga element $x$ och $a$ (för $a \leq b$ ). Ett sådant element kallas ett modulärt element . Ännu mer $generellt (x , b)$ kan den modulära lagen gälla för alla $a$ och ett fixerat par . Ett sådant par kallas ett modulärt par , och det finns olika generaliseringar av modularitet relaterade till detta begrepp och till semimodularitet .

Modulära gitter kallas ibland Dedekind-gitter efter Richard Dedekind , som upptäckte den modulära identiteten i flera motiverande exempel .

Introduktion

Modullagen kan ses som en begränsad associativ lag som förbinder de två gitteroperationerna på samma sätt som den associativa lagen λ(μ x ) = (λμ) x för vektorrum kopplar ihop multiplikation i fältet och skalär multiplikation.

Begränsningen $a \leq b$ är helt klart nödvändig, eftersom den följer av $a \lor (x \land b) = (a \lor x) \land b$ . Med andra ord, inget gitter med mer än ett element uppfyller den obegränsade följden av den modulära lagen.

Det är lätt att se att $a \leq b$ innebär $a \lor (x \land b) \leq (a \lor x) \land b$ i varje gitter. Därför kan även modullagen anges som

Modulär lag (variant): $a \leq b$ innebär $(a \lor x) \land b \leq a \lor (x \land b)$ .

Modullagen kan uttryckas som en ekvation som krävs för att hålla ovillkorligt. Eftersom $a \leq b$ innebär $a = a \land b$ och eftersom $a \land b \leq b$ , ersätt $a$ med $a \land b$ i den definierande ekvationen för modullagen för att få:

Modulär identitet: $(a \land b) \lor (x \land b) = ((a \land b) \lor x) \land b$ .

Detta visar att, med användning av terminologi från universell algebra , bildar de modulära gittren en undervarietet av variationen av gitter. Därför är alla homomorfa bilder, subgitter och direkta produkter av modulära gitter återigen modulära.

Exempel

N ₅ , det minsta icke-modulära gittret: x ∨( a ∧ b ) = x ∨0 = x ≠ b = 1∧ b = ( x ∨ a )∧ b .

Gittret av undermoduler i en modul över en ring är modulärt. Som ett specialfall är gittret av undergrupper av en abelisk grupp modulärt.

Gittret för normala undergrupper i en grupp är modulärt. Men i allmänhet gittret för alla undergrupper i en grupp inte modulärt. Till exempel är gittret av undergrupper av den dihedriska gruppen av ordning 8 inte modulärt.

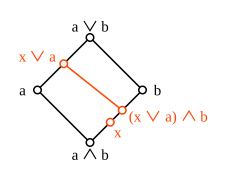
Det minsta icke-modulära gittret är det "femhöriga" gittret N ₅ som består av fem element 0, 1, x , a , b så att 0 < x < b < 1, 0 < a < 1, och a är inte jämförbart med x eller till b . För detta galler,

x ∨ ( a ∧ b ) = x ∨ 0 = x < b = 1 ∧ b = ( x ∨ a ) ∧ b

håller, i strid med modullagen. Varje icke-modulärt gitter innehåller en kopia av N ₅ som ett subgitter.

Egenskaper

Varje distributionsnät är modulärt.

Dilworth (1954) bevisade att, i varje finita modulärt gitter, är antalet sammanfognings-irreducerbara element lika med antalet mötes-irreducerbara element. Mer generellt, för varje $k$ , är antalet element i gittret som täcker exakt $k$ andra element lika med antalet som täcks av exakt $k$ andra element.

En användbar egenskap för att visa att ett gitter inte är modulärt är följande:

Ett gitter

G

är modulärt om och endast om, för alla

a, b, c \in G

,

{\Big (}(c\leq a){\text{ och }}(a\wedge b=c\wedge b){\text{ och }}(a\vee b=c\ vee b){\Big )}\Rightarrow (a=c)

Bevisskiss: Låt G vara modulär och låt premissen för implikationen hålla. Använd sedan absorption och modulär identitet:

c = ( c ∧ b ) ∨ c = ( a ∧ b ) ∨ c = a ∧ ( b ∨ c ) = a ∧ ( b ∨ a ) = a

För den andra riktningen, låt implikationen av satsen gälla i G. Låt a , b , c vara vilka element som helst i G, så att c ≤ a . Låt x = ( a ∧ b ) ∨ c , y = a ∧ ( b ∨ c ). Av den modulära olikheten följer omedelbart att x ≤ y . Om vi visar att x ∧ b = y ∧ b , x ∨ b = y ∨ b , då måste antagandet x = y gälla. Resten av beviset är rutinmässig manipulation med infima, suprema och ojämlikheter. ^{[ citat behövs ]}

Diamond isomorphism theorem

För alla två element a , b i ett modulärt gitter kan man överväga intervallen [ a ∧ b , b ] och [ a , a ∨ b ]. De är förbundna med ordningsbevarande kartor

ψ: [ a φ a ∨ b ] → [ a ∧ b ] b ]

: [ a ∧ b , , → [ a , a ∨ b ] och

som definieras av φ( x ) = x ∨ a och ψ( y ) = y ∧ b .

I ett modulärt gitter är kartorna φ och ψ indikerade med pilarna ömsesidigt omvända isomorfismer.
Misslyckande i diamantisomorfismsatsen i ett icke-modulärt gitter.

Sammansättningen ψφ är en ordningsbevarande karta från intervallet [ a ∧ b , b ] till sig själv som också uppfyller olikheten ψ(φ( x )) = ( x ∨ a ) ∧ b ≥ x . Exemplet visar att denna ojämlikhet generellt sett kan vara strikt. I ett modulnätverk gäller dock jämlikhet. Eftersom dualen av ett modulärt gitter återigen är modulärt, är φψ också identiteten på [ a , a ∨ b ], och därför är de två kartorna φ och ψ isomorfismer mellan dessa två intervall. Detta resultat kallas ibland diamantisomorfismsatsen för modulära gitter. Ett gitter är modulärt om och endast om diamantisomorfismens sats gäller för varje par av element.

Diamant isomorfismsatsen för modulära gitter är analog med den andra isomorfismsatsen i algebra, och det är en generalisering av gittersatsen .

Modulpar och relaterade begrepp

_centrerade hexagongittret S7 , även känt som D2 _, är M-symmetriskt men inte modulärt.

I vilket gitter som helst är ett modulärt par ett par ( a, b ) av element så att för alla x som uppfyller a ∧ b ≤ x ≤ b , har vi ( x ∨ a ) ∧ b = x , dvs om ena halvan av diamanten isomorfism-satsen gäller för paret. Ett element b i ett gitter kallas ett (höger) modulärt element om ( a, b ) är ett modulärt par för alla element a .

Ett gitter med egenskapen att om ( a, b ) är ett modulärt par, då ( b, a ) också är ett modulärt par kallas ett M-symmetriskt gitter . Eftersom ett gitter är modulärt om och endast om alla par av element är modulära, är uppenbarligen varje modulärt gitter M-symmetrisk. I det ovan beskrivna gittret N5 är paret ( b, a ) modulärt, men paret ( a, b ) är det inte _. Därför är N5 inte M-symmetrisk _. Det centrerade hexagongittret S ₇ är M-symmetriskt men inte modulärt. Eftersom N5 är ett subgitter av S7 , följer det att de M-symmetriska gittren inte bildar en undervarietet av variationen av _gitter_.

M-symmetri är inte ett självdubbelt begrepp. Ett dubbelt modulärt par är ett par som är modulärt i det dubbla gittret, och ett gitter kallas dubbelt M-symmetriskt eller M ^* -symmetriskt om dess dual är M-symmetriskt. Det kan visas att ett finit gitter är modulärt om och endast om det är M-symmetriskt och M ^* -symmetriskt. Samma ekvivalens gäller för oändliga gitter som uppfyller det stigande kedjevillkoret (eller det fallande kedjevillkoret).

Flera mindre viktiga föreställningar är också nära besläktade. Ett gitter är tvärsymmetriskt om för varje modulärt par ( a, b ) paret ( b, a ) är dubbelt modulärt. Korssymmetri innebär M-symmetri men inte M ^* -symmetri. Därför är korssymmetri inte ekvivalent med dubbel korssymmetri. Ett gitter med minsta element 0 är ⊥-symmetriskt om för varje modulpar ( a, b ) som uppfyller a ∧ b = 0 är paret ( b, a ) också modulärt.

Historia

Fritt modulärt gitter genererat av tre element {x,y,z}

Definitionen av modularitet beror på Richard Dedekind , som publicerade de flesta relevanta artiklar efter sin pensionering. I en artikel publicerad 1894 ^{[ citat behövs ]} studerade han gitter, som han kallade dubbla grupper ( tyska : Dualgruppen ) som en del av sin "modulalgebra " och observerade att ideal uppfyller vad vi nu kallar modullagen. Han observerade också att för gitter i allmänhet är den modulära lagen likvärdig med dess dubbla.

I en annan uppsats 1897 studerade Dedekind gittret av divisorer med gcd och lcm som operationer, så att gitterordningen ges av delbarhet. I en utvikning introducerade och studerade han galler formellt i ett allmänt sammanhang. Han observerade att gittret av submoduler i en modul uppfyller den modulära identiteten. Han kallade sådana galler för dubbla grupper av modultyp ( Dualgruppen vom Modultypus ) . Han bevisade också att den modulära identiteten och dess dubbla är likvärdiga.

I samma artikel undersökte Dedekind också följande starkare form av den modulära identiteten, som också är självdual:

( x ∧ b ) ∨ ( a ∧ b ) = [ x ∨ a ] ∧ b .

Han kallade gitter som tillfredsställer denna identitet dubbla grupper av idealtyp ( Dualgruppen vom Idealtypus ) . I modern litteratur kallas de oftare för distributionsgitter . Han gav exempel på ett gitter som inte är modulärt och på ett modulärt gitter som inte är av idealtyp.

En artikel publicerad av Dedekind 1900 hade gitter som sitt centrala ämne: Han beskrev det fria modulära gitter som genereras av tre element, ett gitter med 28 element (se bild).

Se även

Modulär graf , en klass av grafer som inkluderar Hasse-diagrammen för modulära gitter
Young–Fibonacci gitter , ett oändligt modulärt gitter definierat på strängar med siffrorna 1 och 2
Ortomodulärt gitter
Iwasawa-gruppen

Anteckningar

^ "Varför är modulära gitter viktiga?" . Matematik Stack Exchange . Hämtad 2018-09-17 .
^ Följande gäller för alla gitter: $a \lor (x \land b) \leq (a \lor x) \land (a \lor b)$ . Närhelst $a \leq b$ , då $a \lor b = b$ .
^ Blyth, TS (2005). "Modulära gitter" . Gitter och ordnade algebraiska strukturer . Universitext. London: Springer. Sats 4.4. doi : 10.1007/1-84628-127-X_4 . ISBN 978-1-85233-905-0 .
^ Blyth, TS (2005). "Modulära gitter" . Gitter och ordnade algebraiska strukturer . Universitext. London: Springer. sid. 65. doi : 10.1007/1-84628-127-X_4 . ISBN 978-1-85233-905-0 .
^ I ett distributionsgitter gäller följande: $(a\wedge b) \vee (x\wedge b)=((a\wedge b)\vee x)\wedge ((a\wedge b)\vee b)$ . Dessutom gäller absorptionslagen, ${\displaystyle (a\wedge b)\vee b=b} ,$ för alla gitter. Att ersätta detta med den andra konjunkten på höger sida av den tidigare ekvationen ger den modulära identiteten.
^ Dilworth, RP (1954), "Proof of a conjecture on finite modular lattices", Annals of Mathematics , Second Series, 60 (2): 359–364, doi : 10.2307/1969639 , JSTOR 1969639 , MR 800 , MR 800 . Omtryckt i Bogart, Kenneth P.; Freese, Ralph; Kung, Joseph PS, red. (1990), "Proof of a Conjecture on Finite Modular Lattices", The Dilworth Theorems: Selected Papers of Robert P. Dilworth , Contemporary Mathematicians, Boston: Birkhäuser, s. 219–224, doi : 10.1007/978-1-4899 3558-8_21 , ISBN 978-1-4899-3560-1
^ Den franska termen för modulärt par är koppla modulärt . Ett par ( a, b ) kallas ett par modulärt på franska om både ( a, b ) och ( b, a ) är modulära par.
^ Vissa författare, t.ex. Fofanova (2001), hänvisar till sådana galler som semimodulära gitter . Eftersom varje M-symmetriskt gitter är semimodulärt och det omvända gäller för gitter med ändlig längd, kan detta bara leda till förvirring för oändliga gitter.
^ ^a ^b ^c ^d ^e ^f ^g Dedekind, Richard (1897), "Über Zerlegungen von Zahlen durch ihre grössten gemeinsamen Theiler" (PDF) , Festschrift der Herzogl. Technischen Hochschule Carolo-Wilhelmina bei Gelegenheit der 69. Versammlung Deutscher Naturforscher und Ärzte i Braunschweig , Friedrich Vieweg und Sohn
^ Dedekind, Richard (1900), "Über die von drei Moduln erzeugte Dualgruppe" , Mathematische Annalen , 53 (3): 371–403, doi : 10.1007/BF01448979 , S2CID 122529830

Corry, Leo (2003-11-27), Modern algebra and the rise of matematical structures (2nd ed.), s. 121–129, ISBN 978-3-7643-7002-2
Fofanova, T. S. (2001) [1994], "Semi-modular lattice" , Encyclopedia of Mathematics , EMS Press
Maeda, Shûichirô (1965), "Om symmetrin av det modulära förhållandet i atomiska gitter", Journal of Science vid Hiroshima University , 29 : 165–170
Rota, Gian-Carlo (1997), "The many lives of lattice theory" (PDF) , Notices of the American Mathematical Society , 44 (11): 1440–1445, ISSN 0002-9920
Skornyakov, L. A. (2001) [1994], "Modular lattice" , Encyclopedia of Mathematics , EMS Press
Stern, Manfred (1999), Semimodular lattices , Cambridge University Press , ISBN 978-0-521-46105-4

externa länkar

"Modulärt gitter" . PlanetMath .
OEIS -sekvens A006981 (Antal omärkta modulära gitter med n element)
Free Modular Lattice Generator En webbläsarbaserad webbapplikation med öppen källkod som kan generera och visualisera några gratis modulära gitter.

[1] "Varför är modulära gitter viktiga?" . Matematik Stack Exchange . Hämtad 2018-09-17 .

[2] Följande gäller för alla gitter: $a \lor (x \land b) \leq (a \lor x) \land (a \lor b)$ . Närhelst $a \leq b$ , då $a \lor b = b$ .

[:0-3] Blyth, TS (2005). "Modulära gitter" . Gitter och ordnade algebraiska strukturer . Universitext. London: Springer. Sats 4.4. doi : 10.1007/1-84628-127-X_4 . ISBN 978-1-85233-905-0 .

[4] Blyth, TS (2005). "Modulära gitter" . Gitter och ordnade algebraiska strukturer . Universitext. London: Springer. sid. 65. doi : 10.1007/1-84628-127-X_4 . ISBN 978-1-85233-905-0 .

[5] I ett distributionsgitter gäller följande: $(a\wedge b) \vee (x\wedge b)=((a\wedge b)\vee x)\wedge ((a\wedge b)\vee b)$ . Dessutom gäller absorptionslagen, ${\displaystyle (a\wedge b)\vee b=b} ,$ för alla gitter. Att ersätta detta med den andra konjunkten på höger sida av den tidigare ekvationen ger den modulära identiteten.

[6] Dilworth, RP (1954), "Proof of a conjecture on finite modular lattices", Annals of Mathematics , Second Series, 60 (2): 359–364, doi : 10.2307/1969639 , JSTOR 1969639 , MR 800 , MR 800 . Omtryckt i Bogart, Kenneth P.; Freese, Ralph; Kung, Joseph PS, red. (1990), "Proof of a Conjecture on Finite Modular Lattices", The Dilworth Theorems: Selected Papers of Robert P. Dilworth , Contemporary Mathematicians, Boston: Birkhäuser, s. 219–224, doi : 10.1007/978-1-4899 3558-8_21 , ISBN 978-1-4899-3560-1

[7] Den franska termen för modulärt par är koppla modulärt . Ett par ( a, b ) kallas ett par modulärt på franska om både ( a, b ) och ( b, a ) är modulära par.

[8] Vissa författare, t.ex. Fofanova (2001), hänvisar till sådana galler som semimodulära gitter . Eftersom varje M-symmetriskt gitter är semimodulärt och det omvända gäller för gitter med ändlig längd, kan detta bara leda till förvirring för oändliga gitter.

[Dedekind.1897-9] ^ ^a ^b ^c ^d ^e ^f ^g Dedekind, Richard (1897), "Über Zerlegungen von Zahlen durch ihre grössten gemeinsamen Theiler" (PDF) , Festschrift der Herzogl. Technischen Hochschule Carolo-Wilhelmina bei Gelegenheit der 69. Versammlung Deutscher Naturforscher und Ärzte i Braunschweig , Friedrich Vieweg und Sohn

[10] Dedekind, Richard (1900), "Über die von drei Moduln erzeugte Dualgruppe" , Mathematische Annalen , 53 (3): 371–403, doi : 10.1007/BF01448979 , S2CID 122529830