Linjär seismisk inversion

Invers modellering är en matematisk teknik där syftet är att bestämma de fysiska egenskaperna hos underytan av en jordregion som har producerat ett givet seismogram . Cooke och Schneider (1983) definierade det som en beräkning av jordens struktur och fysiska parametrar från någon uppsättning observerade seismiska data. Det underliggande antagandet i denna metod är att de insamlade seismiska data är från en jordstruktur som matchar tvärsnittet beräknat från inversionsalgoritmen . Några vanliga jordegenskaper som inverteras för inkluderar akustisk hastighet, formation och vätskedensiteter , akustisk impedans , Poissons förhållande , formationens kompressibilitet, skjuvstyvhet, porositet och vätskemättnad.

Metoden har länge varit användbar för geofysiker och kan kategoriseras i två breda typer: deterministisk och stokastisk inversion. Deterministiska inversionsmetoder baseras på jämförelse av utdata från en jordmodell med observerade fältdata och kontinuerlig uppdatering av jordmodellens parametrar för att minimera en funktion, vilket vanligtvis är någon form av skillnad mellan modellutdata och fältobservation. Som sådan är denna metod för inversion som linjär inversion faller under, som ett minimeringsproblem och den accepterade jordmodellen är den uppsättning modellparametrar som minimerar den objektiva funktionen för att producera ett numeriskt seismogram som bäst jämförs med insamlad seismisk fältdata.

Å andra sidan används stokastiska inversionsmetoder för att generera begränsade modeller som används i reservoarflödessimulering , med hjälp av geostatistiska verktyg som kriging . I motsats till deterministiska inversionsmetoder som producerar en enda uppsättning modellparametrar, genererar stokastiska metoder en svit av alternativa jordmodellparametrar som alla följer modellbegränsningen. De två metoderna är dock relaterade eftersom resultaten av deterministiska modeller är genomsnittet av alla möjliga icke-unika lösningar av stokastiska metoder. Eftersom seismisk linjär inversion är en deterministisk inversionsmetod, kommer den stokastiska metoden inte att diskuteras bortom denna punkt.

Figur 1: Linjärt seismisk inversionsflödesschema

Linjär inversion

Den deterministiska karaktären av linjär inversion kräver ett funktionellt samband som modellerar, i termer av jordmodellens parametrar , den seismiska variabeln som ska inverteras. Detta funktionella förhållande är någon matematisk modell som härrör från fysikens grundläggande lagar och kallas oftare en framåtmodell. Syftet med tekniken är att minimera en funktion som är beroende av skillnaden mellan faltningen av den framåtriktade modellen med en källvåg och det fältinsamlade seismiska spåret . Liksom inom området för optimering kallas denna funktion som ska minimeras den objektiva funktionen och i konvektionsinversmodellering är helt enkelt skillnaden mellan den konvolverade framåtmodellen och den seismiska kurvan. Som tidigare nämnts kan olika typer av variabler inverteras för men för tydlighetens skull kommer dessa variabler att kallas impedansserien för jordmodellen. I de följande underavsnitten kommer vi att beskriva mer i detalj, i samband med linjär inversion som ett minimeringsproblem, de olika komponenterna som är nödvändiga för att invertera seismiska data.

Framåt modell

Mittpunkten i seismisk linjär inversion är den framåtriktade modellen som modellerar genereringen av de experimentella data som samlats in. Enligt Wiggins (1972) ger den ett funktionellt (beräkningsmässigt) samband mellan modellparametrarna och beräknade värden för de observerade spåren. Beroende på de seismiska data som samlats in, kan denna modell variera från de klassiska vågekvationerna för att förutsäga partikelförskjutning eller vätsketryck för ljudvågsutbredning genom berg eller vätskor, till vissa varianter av dessa klassiska ekvationer. Till exempel är den framåtriktade modellen i Tarantola (1984) vågekvationen för tryckvariation i ett flytande medium under seismisk vågutbredning medan Kanasewich och Chiu (1985) genom att anta konstanta hastighetsskikt med plangränssnitt använde brachistotronmodellen av John Bernoulli för färdtiden för en stråle längs en väg. I Cooke och Schneider (1983) är modellen en syntetisk spårgenereringsalgoritm uttryckt som i Eqn. 3, där R(t) genereras i Z-domänen genom rekursiv formel. I vilken form den framåtriktade modellen än uppträder är det viktigt att den inte bara förutsäger den insamlade fältdatan, utan också modellerar hur data genereras. Sålunda kan framåtmodellen av Cooke och Schneider (1983) endast användas för att invertera CMP-data eftersom modellen alltid antar ingen spridningsförlust genom att efterlikna svaret från en lateralt homogen jord på en planvågskälla

1. $t= \sum _{i=1}^{n}{\frac {{\big [}(x_{i}-x_{i-1})^{2}+(y_{i}-y_{i-1 })^{2}+(z_{i}-z_{i-1})^{2}{\big ]}^{\frac {1}{2}}}{v_{i}}}$
där t är strålens gångtid, x, y, z är djupkoordinater och vi är den konstanta hastigheten mellan gränssnitten i − 1 och i.
2. $\left[{\frac { 1}{K({\vec {r}})}}{\frac {\partial ^{2}}{\partial t^{2}}}-\nabla \cdot {\big (}{\frac { 1}{\rho ({\vec {r}}{\big )}}}\nabla )\right]U({\vec {r}},t)=s({\vec {r}},t )$
där $K({\vec {r}})$ representerar bulkmodul, $\rho ({\vec {r}})$ densitet, $s({\vec {r}},t)$ källan till akustiska vågor, och $U({\vec {r}},t)$ den tryckvariation.
3. $s(t)=w(t)*R(t)$

där s ( t ) = syntetiskt spår, w ( t ) = källvåg och R ( t ) = reflektivitetsfunktion.

Objektiv funktion

En viktig numerisk process i invers modellering är att minimera den objektiva funktionen, som är en funktion definierad i termer av skillnaden mellan den insamlade seismiska fältdatan och den numeriskt beräknade seismiska datan. Klassiska objektivfunktioner inkluderar summan av kvadrerade avvikelser mellan experimentella och numeriska data, som i minsta kvadratmetoden , summan av storleken på skillnaden mellan fältdata och numeriska data, eller någon variant av dessa definitioner. Oavsett vilken definition som används erhålls numerisk lösning av det omvända problemet som jordmodell som minimerar objektivfunktionen.

Förutom den objektiva funktionen är andra begränsningar som kända modellparametrar och kända skiktgränssnitt i vissa områden på jorden också inkorporerade i den omvända modelleringsproceduren. Dessa begränsningar, enligt Francis 2006, hjälper till att minska inversionslösningens icke-unikhet genom att tillhandahålla a priori information som inte finns i den inverterade data medan Cooke och Schneider (1983) rapporterar att de är användbara för att kontrollera brus och när de arbetar i en geofysiskt välkänt område.

Matematisk analys av generaliserad linjär inversionsprocedur

Syftet med matematisk analys av invers modellering är att gjuta det generaliserade linjära inversa problemet till en enkel matrisalgebra genom att beakta alla komponenter som beskrivits i tidigare avsnitt. nämligen; framåtmodell, objektivfunktion etc. Generellt är de numeriskt genererade seismiska data icke-linjära funktioner av jordmodellens parametrar. För att ta bort olinjäriteten och skapa en plattform för tillämpning av linjära algebrakoncept linjäriseras den framåtriktade modellen genom expansion med hjälp av en Taylor-serie som utförs nedan. För mer information se Wiggins (1972), Cooke och Schneider (1983).

Betrakta en uppsättning $m$ seismiska fältobservationer $F_{j}$ , för $j=1,\ldots ,m$ och en uppsättning av ${ \displaystyle n}$ jordmodellparametrar $p_{i}$ som ska inverteras för $i=1,\ldots ,n$ . Fältobservationerna kan representeras i antingen ${\vec {F}}\,({\vec {p}})$ eller $F_{j} \,(p_{i})$ , där ${\vec {p}}$ och ${\vec {F}}\,({\vec {p} })$ är vektorrepresentationer av modellparametrar och fältobservationer som en funktion av jordparametrar. På liknande sätt, för $q_{i}$ som representerar gissningar av modellparametrar, är ${\vec {F}}\,({\vec {q}})$ vektorn av numeriska beräknade seismiska data med användning av framåtmodellen av Sec. 1.3. Taylors serieexpansion av ${\vec {F}}\,({\vec {p}})$ om ${\vec {q}}$ ges nedan.

4. ${\vec {F}}\,({\vec {p}})={\vec {F}}\,({\vec {q} })+({\vec {p}}-{\vec {q}}){\frac {\partial {\vec {F}}\,({\vec {q}})}{\partial {\ vec {p}}}}+({\vec {p}}-{\vec {q}})^{2}{\frac {\partial ^{2}{\vec {F}}\,({ \vec {q}})}{\partial {\vec {p}}^{2}}}+O({\vec {p}}-{\vec {q}})^{3}$
Vid linearisering genom att ta bort de icke-linjära termerna (termer med (p⃗ − ⃗q) av ordning 2 och högre), blir ekvationen
5. ${\vec {F}}\,({\vec {p} })-{\vec {F}}\,({\vec {q}})=({\vec {p}}-{\vec {q}}){\frac {\partial {\vec {F }}\,({\vec {q}})}{\partial {\vec {p}}}}$
Med tanke på att ${\vec {F}}$ har $m$ -komponenter och ${\vec {p}}$ och ${\vec {q}}$ har $n$ komponenter, den diskreta formen av Eqn. 5 resulterar i ett system av $m$ linjära ekvationer i $n$ variabler vars matrisform visas nedan.
6. $\Delta {\vec {F}}=\mathbf {A} \,\Delta {\vec {p}}$
7. $\Delta {\vec {F}}={\begin{ bmatrix}F_{1}({\vec {p}})-F_{1}({\vec {q}})\\\vdots \\F_{m}({\vec {p}})-F_ {m}({\vec {q}})\end{bmatrix}}$
8. $\Delta {\vec {p}}={\vec {p}}-{\vec {q} }={\begin{bmatrix}p_{1}-q_{1}\\\vdots \\p_{n}-q_{n}\end{bmatrix}}$
9. $\mathbf {A} ={\begin{bmatrix}{\frac {\partial F_{1}({\vec {q}})}{\partial p_{1}}}&{\frac {\partial F_{1}({\vec {q}})}{\partial p_{2}}}&\cdots &{\frac {\partial F_{1} ({\vec {q}})}{\partial p_{n}}}\\{\frac {\partial F_{2}({\vec {q}})}{\partial p_{1}}} &\cdots &{\frac {\partial F_{2}({\vec {q}})}{\partial p_{n-1}}}&{\frac {\partial F_{2}({\vec {q}})}{\partial p_{n}}}\\\vdots &{\frac {\partial F_{j}({\vec {q}})}{\partial p_{i}}}& \vdots &\vdots \\{\frac {\partial F_{m}({\vec {q}})}{\partial p_{1}}}&{\frac {\partial F_{m}({\ vec {q}})}{\partial p_{2}}}&\cdots &{\frac {\partial F_{m}({\vec {q}})}{\partial p_{n}}}\ \\end{bmatrix}}$

$\Delta {\vec {F}}$ kallas skillnadsvektorn i Cooke och Schneider (1983). Den har en storlek på $m\times 1$ och dess komponenter är skillnaden mellan det observerade spåret och de numeriskt beräknade seismiska data. $\Delta {\vec {p}}$ är korrigeringsvektorn med storleken $n\times 1$ , medan $\mathbf {A}$ kallas känslighetsmatrisen . Den har en storlek på $m\times n$ och dess kommentarer är sådana att varje kolumn är den partiella derivatan av en komponent av framåtfunktionen med avseende på en av de okända jordmodellparametrarna. På liknande sätt är varje rad den partiella derivatan av en komponent av det numeriskt beräknade seismiska spåret med avseende på alla okända modellparametrar.

Lösningsalgoritm

${\vec {F}}\,({\vec {q}})$ beräknas från den framåtriktade modellen, medan ${\vec {F }}\,({\vec {p}})$ är experimentdata. Således $\Delta {\vec {F}}$ en känd kvalitet. Å andra sidan $\Delta {\vec {p}}$ okänd och erhålls genom lösning av ekv. 10. Denna ekvation är teoretiskt lösbar endast när $\mathbf {A}$ är inverterbar, det vill säga om den är en kvadratisk matris så att antalet observationer $m$ är lika med talet ${ \displaystyle n}$ av okända jordparametrar. Om så är fallet, löses den okända korrigeringsvektorn ${\displaystyle \Delta {\vec {p}}} ,$ som visas nedan, med någon av de klassiska direkta eller iterativa lösarna för lösning av en uppsättning linjära ekvationer.

10. $\Delta {\vec {p}}=\mathbf {A} ^{-1}\,\Delta {\vec {F}}$

I de flesta seismiska inversionsapplikationer finns det fler observationer än antalet jordparametrar som ska inverteras för, dvs $m>n$ , vilket leder till ett ekvationssystem som är matematiskt överbestämt. Som ett resultat av detta har Eqn. 10 är inte teoretiskt lösbar och en exakt lösning kan inte erhållas. En uppskattning av korrigeringsvektorn erhålls genom att använda minsta kvadraters proceduren för att hitta korrigeringsvektorn $\Delta {\vec {p}}$ som minimerar ${\vec {e} }\,^{T}{\vec {e}}$ , som är summan av kvadraterna på felet, ${\vec {e}}$ .

Felet ${\vec {e}}$ ges av

11. ${\vec {e}}=\Delta {\vec {F}}-\mathbf {A} \,\Delta {\vec {p}}$

I minsta kvadratmetoden erhålls korrigeringsvektorn som minimerar ${\vec {e}}\,^{T}{\vec {e}}$ enligt nedan.

12. ${\begin{aligned}\mathbf {A} \,\Delta {\vec {p}}&=\Delta { \vec {F}}\\\mathbf {A} ^{T}\mathbf {A} \,\Delta {\vec {p}}&=\mathbf {A} ^{T}\Delta {\vec { F}}\end{aligned}}$

Således,

13. $\Delta {\vec {p}}=(\mathbf {A} ^{T}\mathbf {A} )^{-1} \,\mathbf {A} ^{T}\Delta {\vec {F}}$

Från diskussionerna ovan definieras objektivfunktionen som antingen $L_{1}$ eller $L_{2}$ -normen för $\Delta {\vec {p} }$ ges av $\sum _{j=0}^{n}|\Delta p_{j}|$ eller $\sum _{j=0}^{n}|\Delta p_{j}|^{2}$ eller av $\Delta {\vec {F}}$ ges av $\sum _{i=0}^{m}|\Delta F_{i}|$ eller $\sum _{i=0}^{m}|\Delta F_{i}|^{2}$ .

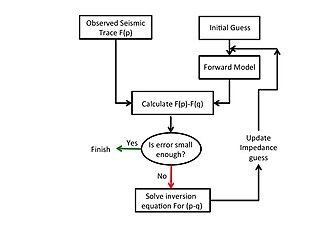
Den generaliserade proceduren för att invertera eventuella experimentella seismiska data för $m=n$ eller ${\displaystyle m>n} ,$ med hjälp av den matematiska teorin för invers modellering, som beskrivits ovan, visas i fig. 1 och beskrivs enligt följande.

En första gissning av modellimpedansen tillhandahålls för att initiera inversionsprocessen. Frammodellen använder denna initiala gissning för att beräkna en syntetisk seismisk data som subtraheras från de observerade seismiska data för att beräkna skillnadsvektorn.

1. En första gissning av modellimpedansen ${\vec {q}}$ ges för att initiera inversionsprocessen.
2. En syntetisk seismisk data ${\vec {F}}({\vec {q}})$ beräknas av den framåtriktade modellen, med hjälp av modellimpedansen ovan.
3. Skillnadsvektorn ${\vec {F}}({\vec {p}})-{\vec {F}}({\vec {q} })$ beräknas som skillnaden mellan experimentell och syntetisk seismisk data.
4. Känslighetsmatrisen $\mathbf {A}$ beräknas till detta värde på impedansprofilen.
5. Med hjälp av $\mathbf {A}$ och skillnadsvektorn från 3 ovan, beräknas korrigeringsvektorn ${\displaystyle \Delta {\vec {p}}}.$ En ny impedansprofil erhålls som
   14. ${\vec {p}}={\vec {q}}+\Delta {\vec {p}}$
6. L $L_{1}$ eller $L_{2}$ för den beräknade korrigeringsvektorn jämförs med ett tillhandahållet toleransvärde. Om den beräknade normen är mindre än toleransen, avslutas den numeriska proceduren och den inverterade impedansprofilen för jordområdet ges av ${\vec {p}}$ från Eqn. 14. Å andra sidan, om normen är större än toleransen, upprepas iterationer genom steg 2-6 men med en uppdaterad impedansprofil beräknad från Eqn. 14. Fig. 2 visar ett typiskt exempel på impedansprofiluppdatering under successiv iterationsprocess. Enligt Cooke och Schneider (1983) användes den korrigerade gissningen från Eqn. 14 eftersom den nya initiala gissningen under iteration minskar felet.

Parametrisering av jordmodellens rymd

Oavsett vilken variabel som ska inverteras för är jordens impedans en kontinuerlig funktion av djupet (eller tiden i seismiska data) och för att numerisk linjär inversionsteknik ska vara tillämplig för denna kontinuerliga fysiska modell måste de kontinuerliga egenskaperna diskretiseras och/eller provtas med diskreta intervall längs jordmodellens djup. Det totala djupet över vilket modellegenskaper ska bestämmas är alltså en nödvändig utgångspunkt för diskretiseringen. Vanligtvis, som visas i fig. 3, samplas dessa egenskaper med nära diskreta intervall över detta djup för att säkerställa hög upplösning av impedansvariation längs jordens djup. Impedansvärdena inverterade från algoritmen representerar medelvärdet i det diskreta intervallet.

Med tanke på att inversmodelleringsproblemet endast är teoretiskt lösbart när antalet diskreta intervall för sampling av egenskaperna är lika med antalet observationer i spåret som ska inverteras, kommer en högupplöst sampling att leda till en stor matris som kommer att bli mycket dyr för att invertera. Vidare kan matrisen vara singular för beroende ekvationer, inversionen kan vara instabil i närvaro av brus och systemet kan vara underbegränsat om andra parametrar än de primära variablerna inverterade för önskas. I förhållande till önskade parametrar, andra än impedans, ger Cooke och Schneider (1983) dem att inkludera source wavelet och skalfaktor.

Slutligen, genom att behandla begränsningar som kända impedansvärden i vissa lager eller diskreta intervall, reduceras antalet okända impedansvärden som ska lösas för, vilket leder till större noggrannhet i resultaten av inversionsalgoritmen.

Figur 8: Amplitudlogg

Figur 9a: Impedansloggar inverterade från amplitud

Figur 9b: Impedansbrunnslogg

Inversionsexempel

Temperaturinversion från Marescot (2010)

Vi börjar med ett exempel för att invertera för jordparametervärden från temperaturdjupfördelningen i en given jordregion. Även om detta exempel inte direkt hänför sig till seismisk inversion eftersom inga vandrande akustiska vågor är inblandade, introducerar det inte desto mindre praktisk tillämpning av inversionstekniken på ett sätt som är lätt att förstå, innan man går vidare till seismiska tillämpningar. I det här exemplet mäts jordens temperatur på diskreta platser i ett borrhål genom att placera temperatursensorer i måldjupen. Genom att anta en framåtmodell av linjär fördelning av temperatur med djup, inverteras två parametrar för från temperaturdjupmätningarna.

Framåtmodellen ges av

15. ${\vec {F}}({\vec {q}})={\vec {T}}=a+bz$

där ${\vec {q}}=[a,b]$ . Således är dimensionen för ${\vec {q}}$ 2, dvs antalet parametrar som inverteras för är 2.

Syftet med denna inversionsalgoritm är att hitta ${\vec {p}}$ , vilket är värdet på $[a,b]$ som minimerar skillnaden mellan den observerade temperaturen distribution och de erhållna med hjälp av framåtmodellen av Eqn. 15. Med tanke på att den framåtriktade modellens dimension eller antalet temperaturobservationer är $n$ skrivs komponenterna i den framåtriktade modellen som

16. ${\begin{aligned}T_{1} &=a+bz_{1}\\T_{2}&=a+bz_{2}\\\vdots \\T_{n-1}&=a+bz_{n-1}\\T_{n} &=a+bz_{n}\\\end{aligned}}$
så att ${\vec {F}}({\vec {q}})=T$
17. $\mathbf {A} ={\begin{bmatrix}1&z_{1}\\1&z_{2}\\\vdots & \vdots \\1&z_{n-1}\\1&z_{n}\\\end{bmatrix}}$

Vi presenterar resultat från Marescot (2010) för fallet med $n=2$ för vilka de observerade temperaturvärdena på djup var $T_{1}=19^{\circ }C$ vid $z=2m$ och $T_{2}=22^{\circ }C$ vid $z=8m$ . Dessa experimentella data inverterades för att erhålla jordparametervärden på $a=0,5$ och $b=18^{\circ }C$ . För ett mer allmänt fall med ett stort antal temperaturobservationer visar fig. 4 den slutliga linjära framåtmodellen som erhålls genom att använda de inverterade värdena för $a$ och $b$ . Figuren visar en bra matchning mellan experimentella och numeriska data.

Inversion av vågrestiden från Marescot (2010)

Detta exempel inverterar för jordlagrets hastighet från registrerade seismiska vågor. Fig. 5 visar de initiala hastighetsgissningarna och färdtiderna registrerade från fältet, medan Fig. 6a visar den inverterade heterogena hastighetsmodellen, som är lösningen av inversionsalgoritmen som erhålls efter 30 iterationer . Som framgår av fig. 6b finns det bra jämförelser mellan de slutliga färdtiderna erhållna från den framåtriktade modellen med användning av den inverterade hastigheten och fältregistreringens färdtider. Med hjälp av dessa lösningar rekonstruerades strålbanan och visas vara mycket slingrande genom jordmodellen som visas i fig. 7.

Seismisk spårinversion från Cooke och Schneider (1983)

Detta exempel, hämtat från Cooke och Schneider (1983), visar inversion av en CMP-seismisk kurva för jordmodellimpedansprofilen (produkt av densitet och hastighet). Det inverterade seismiska spåret visas i fig. 8 medan fig. 9a visar den inverterade impedansprofilen med den initiala ingångsimpedansen som används för inversionsalgoritmen. Vid sidan av det seismiska spåret registreras också en impedanslogg för jordområdet, såsom visas i fig. 9b. Figurerna visar bra jämförelse mellan den registrerade impedansloggen och den numeriska inverterade impedansen från det seismiska spåret.

Vidare läsning

• Backus, G. 1970. "Inferens från otillräckliga och felaktiga data." Proceedings of the National Academy of Sciences of the United States of America 65, nr. 1.
• Backus, G. och F. Gilbert. 1968. "The Resolving Power of Gross Earth Data." Geophysical Journal of the Royal Astronomical Society 16 (2): 169–205.
• Backus, GE och JF Gilbert. 1967. "Numeriska tillämpningar av en formalism för geofysiska omvända problem." Geophysical Journal of the Royal Astronomical Society. 13 (1-3): 247.
• Bamberger, A., G. Chavent, C. Hemon och P. Lailly. 1982. "Inversion av normala incidensseisomogram." Geofysik 47 (5): 757–770.
• Clayton, RW och RH Stolt. 1981. "En Born-WKBJ-inversionsmetod för akustisk reflektionsdata." Geofysik 46 (11): 1559–1567.
• Franklin, JN 1970. "Välpositionerade stokastiska förlängningar av illa ställda linjära problem." Journal of Mathematical Analysis and Applications 31 (3): 682.
• Parker, RL 1977. "Understanding invers theory." Annual Review of Earth and planetary sciences 5:35–64.
• Rawlinson, N. 2000. "Inversion of Seismic Dat for Layered Crustal Structure." Ph.D. diss., Monash University.
• Wang, B. och LW Braile. 1996. "Samtidig inversion av reflektions- och refraktionsseismiska data och tillämpning på fältdata från norra Rio Grande-sprickan." Geophysical Journal International 125 (2): 443–458.
• Weglein, AB , HY Zhang, AC Ramirez, F. Liu och JEM Lira. 2009. "Att klargöra den underliggande och grundläggande innebörden av den ungefärliga linjära inversionen av seismiska data." Geofysik 74 (6): 6WCD1–WCD13.