Lattice och bridged-T equalizers

Gitter- och brygg-T-utjämnare är kretsar som används för att korrigera för amplitud- och/eller fasfel i ett nätverk eller en transmissionsledning. Vanligtvis är syftet att uppnå en övergripande systemprestanda med ett platt amplitudsvar och konstant fördröjning över ett föreskrivet frekvensområde, genom tillägg av en utjämnare. Tidigare har designers använt en mängd olika tekniker för att realisera sina equalizerkretsar. Dessa inkluderar metoden för kompletterande nätverk; metoden för raklinjeasymptoter; använda en specialbyggd testjigg; användningen av standardkretsbyggstenar,; eller med hjälp av datorprogram. Dessutom har försök och felmetoder visat sig vara förvånansvärt effektiva, när de utförs av en erfaren designer.

I video- eller ljudkanaler resulterar utjämning i vågformer som sänds med mindre försämring och har skarpare transienta kanter med minskade översvängningar (ringning) än tidigare. I andra tillämpningar, såsom CATV- distributionssystem eller frekvensmultiplexerade telefonsignaler där flera bärvågssignaler skickas, är syftet att utjämna transmissionslinjen så att dessa signaler har ungefär samma amplitud. Gitter- och bryggkopplade-T-kretsarna är gynnade för passiva utjämnare eftersom de kan konfigureras som nätverk med konstant motstånd, såsom Zobel-nätverket , som påpekats av Zobel och senare av Bode .

Enkelordsbeskrivningen "utjämnare" används ofta när huvudsyftet med nätverket är att korrigera amplitudsvaret för ett system, även om viss fördelaktig faskorrigering också kan uppnås samtidigt. När faskorrigering är huvudproblemet används den mer explicita termen "fasutjämnare" eller "faskorrektor". (I det här fallet är kretsen vanligtvis ett allpassnätverk som inte förändrar amplitudsvaret alls, såsom gitterfasutjämnaren ) .

Vid utjämning av en balanserad transmissionsledning är gittret den bästa kretskonfigurationen att använda, medan för en enkeländad krets med ett jordplan är det överbryggade T-nätverket mer lämpligt. Även om utjämnarkretsar, av endera formen, kan utformas för att kompensera för ett brett spektrum av amplitud- och faskarakteristika, kan de bli mycket komplicerade när kompensationsuppgiften är svår, vilket visas senare.

En mängd olika metoder har använts för att designa equalizers och några av dessa beskrivs nedan. Flera av procedurerna går tillbaka till början av 1900-talet då utjämnare behövdes av den snabbt expanderande telefonindustrin. Senare, med tillkomsten av tv, blev utjämningen av videolänkar också mycket viktig.

Amplitudkorrigering

Syftet med ett utjämnarnätverk är att korrigera för brister i amplitudsvaret hos en transmissionsledning, ett nätverk med klumpade element eller förstärkarkedja. Utjämning är ofta nödvändig med transmissionsledningar och fördröjningsledningar med klumpade element som tenderar att ha ökande förluster med frekvensen. Utan korrigering förloras vågformsfideliteten, och stignings- och falltider för transienter försämras (dvs mindre skarpa). Ibland krävs amplitudkorrigering av mer subtila skäl, till exempel, när det gäller analoga färg-TV-vågformer, kan färgfel uppstå i de visade bilderna när överföringssystemets svar inte är platt. Det är vanligt att välja gitter- och brygg-T-utjämnare som är nätverk med konstant motstånd . Det påpekades av Zobel och senare av Bode att sådana nät kan kaskadkopplas med varandra och med en transmissionsledning eller med en krets med klumpar, utan att införa missanpassningsproblem. Användningen av konstanta motståndskonfigurationer har varit vanlig praxis i utjämnardesign i många år, och nästan alla exempel som presenteras i denna artikel har denna egenskap.

Oavsett designmetod introducerar passiva utjämnare alltid ytterligare förluster i överföringsvägen, och detta måste åtgärdas av en förstärkare eller repeater .

Metoden för kompletterande nätverk

I några av sina tidiga arbeten utvecklade Zobel en krets med klumpade element för att simulera beteendet hos en given lång transmissionslinje av intresse. En sådan anordning var användbar genom att den gjorde det möjligt att utföra utredningsarbete på ett transmissionssystem på laboratoriets bekvämlighet. Viktigt, som påpekades av Zobel, när ett sådant nätverk väl hade utformats, var det alltid möjligt att hitta ett realiserbart kompletterande nätverk, som uppvisade det omvända svaret.

Ett exempel

Proceduren kan illustreras med ett enkelt exempel som presenteras av Zobel, vilket visas nedan. Här har det vänstra gittret en enkel lågpasskarakteristik och det högra gittret har den komplementära egenskapen. För denna krets R1*R2 = L1/C1 = L2/C2 = R0^2 med R1 < 2.R0. C2 ges av $C_{2}={\Big [}{\Big (}{\frac {R_{0}}{R_{1}}}{\Big )}^{2}-1{ \Big ]}.{\frac {L_{1}}{R_{0}^{2}}}$

Kaskad av lågpass- och högpassgitter

Individuella och övergripande svar

För ett normaliserat nätverk R0 = 1Ω. Välj R1 = 0,5Ω och L1 = 1H, sedan R2 = 2Ω, C1 = 1F, C2 = 3F och L2 = 3H

Svaren från de enskilda sektionerna och den övergripande responsen visas i diagrammen för det sammansatta nätverket, till höger.

₀ Denna kompensationsprocess kan beskrivas matematiskt, med hjälp av de grundläggande gitterekvationerna som ges i gitternätverket , enligt följande. Transmissionsförlusten för ett normaliserat (R = 1) konstant motståndsgitter med genomgående armar Z _a och tvärdiagonala armar av Z _b är

$T(p)={\frac {1-z_{a}}{1+z_{a}}} ={\frac {z_{b}-1}{z_{b}+1}}$

Nu för lågpasskretsen, som ges ovan, är za en parallell kombination av ett 0,5Ω motstånd parallellt med 1H induktor.

$z_{a}(lågpass)={\frac {0.5\times p}{0.5+p} }={\frac {p}{1+2.p}}$

och så

$T(lågpass)={\frac {1-{\frac {p}{(1+2.p}}}{1+{\frac {p}{(1+2.p)}}}}={\frac {1+p}{ 1+3.p}}$ Tänk sedan på högpasssektionen. Här är za en parallell kombination av ett 0,5Ω motstånd parallellt med en 3F kondensator, så

$z_{a}(highpass)={\frac {0.5 \times 1/3.p}{0.5+1/3.p}}={\frac {1}{2+3.p}}$

och så

$T(highpass)={\frac {1-1/(2+3.p)}{1+1/(2+3.p)}}={\frac { 1+3.p}{3+3.p}}={\frac {1+3.p}{3(1+p)}}$

Slutligen är det övergripande svaret Ttot $T_{tot}(p)=T(lågpass)\ gånger T(högpass)={\frac {1+p}{1+3.p}}\ gånger {\frac {1+3.p}{3(1+p)}}={\frac {1}{3}}$ dvs ett platt svar, med en total förstärkning på en tredjedel. Detta visas i figuren ovan. I detta exempel är den övergripande karakteristiken faslös, dvs full faskompensation har uppnåtts utöver amplitudkorrigeringen. Detta beror på att exakt korrigering har uppnåtts vid alla frekvenser. Ofta är korrigering endast framgångsrik över ett begränsat frekvensområde, i vilket fall det slutliga resultatet kommer att ha en viss restfas.

Mer generellt kan svaret från en krets eller transmissionsledning vara svårt att reproducera exakt med hjälp av kretsar med klumpar, så den vanliga uppgiften är att hitta en realiserbar egenskap som är en acceptabel matchning. Ibland kan testa ett fel metoder, tillämpade på ett systematiskt sätt visa sig framgångsrika

En allmän utjämningskrets

När armarna på ett gitternätverk är rent reaktiva, är konstant motstånd all-pass-nätverk möjliga, som visas i gitterfördröjningsnätverk . Om emellertid motstånd är inkluderade i gitterarmarna, är olika amplitudsvar möjliga samtidigt som den konstanta resistansegenskapen bibehålls.

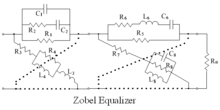
En mycket använd utjämningskrets visas här, tillsammans med motsvarande bryggkopplade T-krets. Ekvivalensen mellan gitter och bryggt-T kan visas med Bartletts bisektionssats . Kretsarna har konstant resistanskarakteristik när Z1.Z2 = R02.

Gemensam Equalizer-krets

Överföringsfunktionen för denna krets är $T(p)={\frac {R_{0}}{R_{0}+Z_{1}(p) }}$

När de är normaliserade så att källan och termineringsmotstånden och R0 alla är ett och Z1.Z2 = 1, blir det $T(p)={\frac {1} {1+Z_{1}(p)}}$

och så Z1, som en funktion av T, ges av $Z_{1}(p)={\frac {1}{T(p)}} -1$

Enkelheten i denna ekvation (endast en impedans måste hittas) gör kretsen populär i utjämningsdesigner.

Metoden för raka asymptoter

Metoden använder ett initialt försökssvar, som består av en sekvens av räta linjeasymptoter, för att bestämma pol/nollplatserna för ett realiserbart nätverk.

De allmänna principerna för metoden är följande.

Enkelpol vid p = -a

Svar av enpol och asymptoter

Betrakta fallet med en enkel RC-lågpasskrets vars överföringsfunktion har en enda pol på den reella frekvensaxeln vid p = -a, som visas. Detta svar är -3 dB vid ω = a och faller med 6 dB per oktav vid hög frekvenser. Den visas plottad, i decibel, kontra frekvens (på en log-skala). Till höger visas också den asymptotiska approximationen med två linjer, med brytfrekvens också vid ω = a. Som kan ses är den sanna responsen och den räta linjens approximation nära överensstämmande över större delen av frekvensområdet, endast avvikande nära ω = a.

Om en nolla nu adderas vid, säg, -10×a, så introduceras en ny asymptot med en positiv lutning på 6 dB per oktav, med start vid ω = 10, som visas.

Pol och nolla

Svar av pol & noll + asymptoter

Genom att utvidga metoden kan en komplicerad förlustkarakteristik approximeras med en sekvens av räta linjeasymptoter förutsatt att förlustkarakteristikens brantaste lutning inte överstiger 6 dB per oktav i frekvensområdet. Resultaten plottas på en dB-skala mot frekvens på en log-skala, som tidigare.

$T(p)={\frac {(p+b)(p+d)(....}{(p+a)(p+ c)(....}}\quad där\ a<b<c<d<....etc.$ överföringsfunktionen

När väl ett uttryck bedöms uppfylla kravet med tillräcklig noggrannhet, kan impedanserna Z1 och Z2 hittas från de tidigare angivna förhållandena.

Ett exempel

Som ett exempel ska överföringsförlusten för ett fiktivt distributionsnät, med svaret som visas med den heldragna linjen i figuren till vänster, korrigeras (utjämnas). I detta exempel krävs korrigering över frekvensområdet från Ω ₁ = 0,09 r/s till Ω ₂ = 140 r/s. Detta kan approximeras av en serie räta linjesegment som visas i figuren. Frekvenser väljs så att de olika felen som uppvisas av den räta linjeapproximationen är alla lika och så små som möjligt.

Respons + asymptotisk ca.

Målrespons och nätverksrespons

Den räta linjens approximation som visas i figuren har poler vid ω = 0,333 r/s och 10 r/s, och nollor vid ω = 1 r/s och 30 r/s.

Överföringsfunktionen för ett nätverk med dessa poler och nollor ges av

$T(p)={\frac {(1+p)(1+0,03333p) )}{(1+3p)(1+0.1p)}}$

Den faktiska responsen (magnituden) för T beräknas lätt och visas, på diagrammet till höger, som en funktion av frekvensen, tillsammans med målresponsen. En närmare passning skulle kräva extra poler och nollor i T(p), på ett närmare avstånd.

Lågpassnätverket T(p), med detta svar, kommer att ha ett LC-nätverk för Z1 och ett RC-nätverk för Z2, när det realiseras med användning av de enkla kretsarna som tidigare beskrivits. Emellertid av mer intresse här är det komplementära nätet, eftersom detta kommer att korrigera för den fallande överföringsförlusten för detta svar.

Överföringsfunktionen för equalizernätverket kommer att vara ${\displaystyle Te(p)={\frac {1}{T(p)}}={\frac {1 }{K}}.{\frac {(1+3p)(1+0.1p)}{(1+p)(1+0.03333p)}}} där K = 9 så att nätverkets förstärkning aldrig$ överstiger enhet vid vilken frekvens som helst.

Uttrycket för Z1(p) kan härledas från denna ekvation med $Z_{1}(p)={\frac {1}{Te(p) }}-1$

Så $Z_{1}(p)={\frac {8+6,2p}{(1+3p)( 1+0,1p)}}$

Z1 kan realiseras som ett RC-stegenätverk (eller som en parallell kombination av två RC-impedanser, som var och en är ett motstånd och en kondensator i serie).

Gitterimpedanser för equalizer

Utjämnad respons

En stegnätverksversion av Z1 visas till vänster, tillsammans med den för Z2 (dess dubbla nätverk). Komponentvärden för Z1 (med R0 = 1) är: C1 = 0,04838F, C2 = 0,4747F, R1 = 2,2857Ω, R2 = 5,7152Ω och för Z2 är de L1 = 0,0438H, L2 = 0,4747H, L2 = 0,4747H, 4 R3750,4 R3750,4. R4 = 0,1750.

Dessa kretsar av Z1 och Z2 kan användas direkt i ett bryggat-T-utjämnarnätverk, men för användning i ett gitternätverk bör kondensatorvärdena fördubblas och motståndsvärdena halveras i Z1-nätverket, och alla motstånds- och induktorvärden fördubblas i Z2 (dvs Za = Z1/2 och Zb = 2,Z2).

Det övergripande svaret, när equalizern är kaskadad med den ursprungliga karakteristiken, visas till höger. Som förväntat finns det rippel på resultatet, vilket liknar skillnaderna mellan det initiala svaret och dess approximation T(p).

Även om svaret, före utjämning, betraktat i detta exempel, har en egenskap som faller linjärt när den plottas mot log(ω), är det möjligt att klara av icke-linjära egenskaper på ungefär samma sätt, förutsatt att plotten faller monotont – dvs. lutningen ändrar inte tecken, och den maximala lutningen är mindre än 6 dB/oktav. I sådana fall kan en serie av räta linjeasymptoter också hittas för att approximera ett svar och på så sätt leda till en realiserbar lösning.

Equalizers av betydande komplexitet kan utformas med hjälp av asymptotmetoden, och de kan uppnå en övergripande, korrigerad respons med mycket låg rippel (<<0,1 dB).

Härleda kompensationsnätverk med hjälp av en experimentell testjigg

En experimentell testjigg kan användas för att hitta komponentvärdena för att hitta kretsvärden för utjämnaren. Det grundläggande kretsarrangemanget visas till vänster.

Schema för utjämningsprovjigg

Överföringsfunktionen för denna enkla krets, ignorerar platt förlust, är $T(p)={\frac {R_{0}}{(R_{0} +2.Z_{x})}}$

Nu, om 2.Zx = Z1, blir detta $T(p)={\frac {R_{0}}{(R_{0}+Z_{1 })}}$

Så T(p) har samma form som överföringsfunktionen för den grundläggande utjämnarkretsen som gavs tidigare med Zx identisk med "Za" gitterarmarna. Så även om testjiggen i sig inte är ett konstant motståndsnätverk tillhandahåller den en bekväm experimentell metod för att bestämma de erforderliga komponentvärdena för en gitter- eller bryggad-T-krets som är ett konstant motståndsnätverk. När värdena för Zx väl är etablerade, hittas kretsvärdena för Z1 och dess dubbla, Z2, på ett enkelt sätt.

Till höger visas ett förslag på testjigg med dessa koncept.

Equalizer testjigg

(i) Den grundläggande RC-kretsen som utgör huvuddelen av Zx är i form av ett stegnätverk, snarare än en parallell kombination av serie-RC-par. Den totala spridningen av kondensatorvärdena som behövs är mycket reducerad för denna konfiguration. Vanligtvis räcker det med ett nätverk av sex eller sju sektioner. (ii) Ett shuntmotstånd R placeras över Zx ingångsterminaler, och detta minskar också spridningen av komponentvärden. Tyvärr minskar den också den maximala korrigeringen som är möjlig av en individuell utjämningssektion och kan resultera i att en kaskad av två eller flera sektioner är nödvändig för att uppnå total utjämning. (iii) En serieresonans LC-krets finns också över terminalerna på Zx. Denna kombination är anordnad att resonera över toppfrekvensen för systemets passband och dess syfte är att reducera utjämnarens flata förlust. (Det är en teknik som vanligtvis används i equalizerkretsar). (iv) Istället för att hitta komponentvärden för att uppnå ett önskvärt frekvenssvar, är ett alternativt tillvägagångssätt att optimera den transienta prestandan, med hjälp av testvågformer (såsom puls- och strecksignaler, till exempel). Att optimera transientprestanda på detta sätt är särskilt tillämpbart i situationer där vågformsfidelitet är viktigt, såsom i TV. När kretsvärden erhålls på detta sätt är beskrivningen "vågformskorrigerare" att föredra framför "svarsutjämnare"

Ett exempel

Ett exempel på en "vågformskorrigerare" för en koaxialkabelsektion för videofrekvenser visas. Shuntimpedansen Z2 visas inte i detalj. Det är dual av Z1, så medan Z1 innehåller en serieresonanskrets och ett RC-stegnätverk, innehåller Z2 en shuntresonanskrets och ett RL-stegnätverk.

Exempel på vågformskorrigerare

Plottet av vout/vin (i dBs) kontra frekvens, för denna krets, med hjälp av de komponentvärden som föreslagits i referensen visas också till höger.

Insättningsförlust av vågformskorrigerare

Zobels kurvanpassningsprocedur

₀
Zobel beskrev i sin tidiga artikel en procedur där en kaskad av prototypnätverk av konstant motståndsnät bildade grunden för hans utjämnare. Hans metod var i grunden en kurvanpassningsprocedur och en bilaga i hans papper gav en serie nätverk från vilka en komplett utjämnare kunde byggas. Han fördelade bidrag till det övergripande önskade utjämnarsvaret till de olika medlemmarna i en gitterkaskad (eller bryggad-T). Varje gitterkrets i kaskaden identifierades av dess impedanser Za _och Zb ₍ där Z _b = R ² /Z _a och genom dess "utbredningsfunktion" och "dämpningskonstant" (i själva verket kvadraten på storleken). bildparametrar... är alla relaterade till varandra som Zobel visade se ( Bildimpedans ). För det första kan gitterimpedansen Za uttryckas som förhållandet mellan två polynom i (jf)

${\displaystyle {$

₀₀ I detta uttryck är impedanskoefficienterna a , b , etc., av vilka en är enhet och några kan vara noll, algebraiska kombinationer av nätverkselementen. För varje given typ av nätverk är koefficienterna fixerade av elementen och vice versa.

För det andra kan utbredningskonstanten Γ hittas från

₀₀₀₀ $e^{ \Gamma }={\frac {g_{0}+g_{1}(jf)+g_{2}(jf^{2}+....}{h_{0}+h_{1}(jf) +h_{2}(jf)^{2}+....}}$ där g , g ₁ ,h , etc. är algebraiska funktioner av a , b , etc. Ur detta kan dämpningskonstanten härledas och uttryckt som en funktion av frekvens (Det var vanligt på 1920-talet att visa dämpning som en positiv parameter, så svaret från ett lågpassfilter visades som en positivt stigande kurva, med ökande frekvens).

För dämpningskonstanten har uttrycket formen:

$F=(e^{A})^{2}=e^{2A}=10^{\frac {TU}{10}}={\frac {P_{0}+P_{2}. f^{2}+P_{4}.f^{4}+....}{Q_{0}+Q_{2}.f^{2}+Q_{4}.f^{4}+ ....}}$ som är ett förhållande mellan två polynom i f ² , och där koefficienterna kunde bestämmas från kända data eller mätningar. Genom att ordna om detta fick Zobel den "linjära dämpningsekvationen", som gäller vid alla frekvenser, sålunda:

₀₀ $P_{0}+f^{2}.P_{2}+....-FQ_{0}-f^{2}Q_{2}-....=0$ Genom att ha dämpning data vid tillräckliga datapunkter (frekvenser), kan en familj av samtidiga ekvationer lösas för att ge värdena för P , Q , P ₂ , Q ₂ , etc. Från dessa resultat visade Zobel, i bilagan till sin artikel hur, t.ex. varje prototyp equalizerkrets, var det möjligt att härleda komponentvärdena för den sektionen.

Ett exempel

Som ett exempel användes proceduren av Zobel för att designa en equalizer för en balanserad linje med en karakteristisk impedans på 600 Ω och 50 miles i längd, för frekvenser upp till 4,5 kHz. I denna tidiga tidning använde Zobel "napier" (den naturliga logaritmen för ett spänningsförhållande) och "överföringsenheten" (en logaritm till basen 10 för ett effektförhållande) omväxlande inom sina beräkningar. De två enheterna är relaterade till 1 napier = 8.686 transmissionsenheter. I mitten av 1920-talet döptes dessa enheter om till "neper" och "decibel" och det är dessa enheter som används här.

Den ursprungliga dämpningskaraktäristiken som kräver korrigering visas som "Plot 1" i figuren nedan.

Zobel telefonlinjeutjämnare

Zobel föreslog att en tillfredsställande utjämnad respons skulle erhållas genom en kaskad av två gitter, av de typer som visas i figuren till vänster. Det vänstra gittret, i figuren, gav korrigering av svaret vid låga frekvenser och det högra gav korrigering vid höga frekvenser.

Med tanke på först den vänstra kretsen har denna en linjär dämpningsekvation

₀₀ $P_{0}+f^{2}.P_{2}-F.Q_{0}-f^{2}.Q_{2}=f^{ 4}(F-1)$ så det finns fyra okända att hitta, P , P ₂ , Q , Q ₂ , och därför krävs data vid fyra frekvenser. Från de uppmätta data på transmissionsledningen föreslog Zobel följande dämpningsvärden. Vid fi ₌ 40 Hz, Ai ₌ 0,536 neper; vid f2 ₌ 200 Hz, A2 ₌ 0,291 neper; vid _f3 = 800 Hz, A3 ₌ 0,176 neper; vid _f4 = 2000 Hz, A4 ₌ 0,100 neper. (Dessa ger ett svar som är det omvända till det för den ursprungliga plotten, som krävs för equalizern, men med en godtycklig 0,1neper offset vid den högsta frekvensen.)

₀₀ Lösningen av de fyra samtidiga ekvationerna härledda från dessa data gav P = 102,007 × 10 ⁹ , Q = 32,20010 × 10 ⁹ , P ₂ = 5,06037 × 10 ⁶ , Q ₂ = 3,43087 × 10 ⁶ , från vilken Zobels designkomponent gav följande designkomponent. värden: C ₁ = 1,2042 μF, R ₁ = 168,32 Ω, C ₂ = 4,0342 μF, R ₂ = 124,19 Ω R ₃ = 2138,72 Ω, L ₃ = 0,433851H , _28,72 Ω, L ₃ = 0,433845 = 5 Ω 4 2 9 H

₀₀ I fallet med det högra gittret valt av Zobel har dämpningskonstanten samma värde vid låga och höga frekvenser, så P = F och den har en topp i svaret nära resonansfrekvensen för C ₆ och L ₆ . Den linjära dämpningsekvationen för detta gitter är

$-P_{2}+F.Q_{2}-f^{2}(F_{0}-F) Q_{4}=(F_{0}-F)/f^{2}$

₀₀₀₀₀₀₀₀ Uttrycket för dämpningskonstanten för det högra gittret har P = F , Q = 1 och P ₄ = F . Q ₄ , så data behövdes för att lösa för P , P ₂ , Q ₂ och Q ₄ . Data som användes var: vid f = 0 Hz, Ai ₌ 0,796 neper; vid fi ₌ 3000 Hz, Ai ₌ 0,747 neper; vid f2 ₌ 4000 Hz, A2 ₌ 0,530 neper; vid _f3 = 4500 Hz, A3 ₌ 0,300 neper. Lösningen av de fyra samtidiga ekvationerna härledda från dessa data gav F = P = 4,913; P2 = -46,207x10-8 ^;_{_} Q2 = -90092×10 ⁻⁸ ; Q4 = 23,198×10 ⁻¹⁶ . Med hjälp av dessa data gav Zobels designekvationer för detta gitter följande komponentvärden: R ₅ = 226.95 Ω, R ₆ = 143.4 Ω, L ₆ = 0.04935H, C _{6 =} .02476 μF R _{7 =}_1586,5 Ω 5 Ω , L ₈ = 8,8992 mH, C ₈ = 0,137 μF

De slutliga resultaten visas i figuren nedan. Plot 1 i figuren visar det initiala svaret för kabeldragningen som skulle korrigeras. Kompensationen som uppnås av det vänstra (lågfrekventa) gittret, enbart, visas i plot 2. Slutligen visas total kompensation i plot 3, när det högra gitter också ingår.

Bodes metod för utjämning

Bode ägnade kapitel XII i sin välkända bok åt ämnet equalizers. Han påpekade att alla överföringsfunktioner kan utgöras av en kaskad av första och andra ordningens konstantmotståndsgitter som naturligtvis inkluderar utjämnarnätverk. För att hjälpa till med processen för nätverksdesign tillhandahöll Bode designdetaljer för fyra första och fyra andra ordningens nätverk för att täcka de olika möjliga platserna för polerna och nollorna i det komplexa frekvensplanet. Tyvärr härleddes några av de kretsar han föreslog (när pol- och nolllägen var komplexa), med hjälp av Brunes syntesmetod, som ibland producerade gitterimpedanser som innehåller ömsesidigt kopplade spolar. Ett senare dokument tillhandahåller dock alternativa nätverk för att undvika detta problem.

Ett exempel

Som ett exempel på metoden, betrakta realiseringen av det enkla utjämnarsvaret som gavs tidigare. Det kan realiseras med hjälp av enkla gitter i kaskad. Svaret som krävs är

$Te(p)={\frac {1}{T(p)}}={\frac {1} {9}}.{\frac {(1+3p)(1+0.1p)}{(1+p)(1+0.03333p}}$ Detta kan skrivas om så här

$Te(p)={\frac {(p+0.3333p)}{(1+p)}}.{\frac {(p+10)}{( p+30)}}$ Detta kan fördelas på två första ordningens gitter i kaskad, med hjälp av typ IV-kretsarna från Bodes diagram för att ge den visade kretsen.

Bode equalizer (galler)

Bode equalizer (bryggad-T)

Detta kan enkelt konverteras till en kaskad av standardkonstant motstånd överbryggade-T-sektioner av den form som beskrivits tidigare, som visas till höger. (En enklare krets är också möjlig, som använder färre motstånd).

Utveckling av en equalizer genom kretsförfining

Utöver de metoder som beskrivits tidigare, kan en slutlig utjämnarkrets erhållas genom att först börja med en initial enkel lösning och sedan använda en process för kretsförfining för att öka komplexiteten hos kretsen och dess respons, tills en tillfredsställande prestanda erhölls. Ett exempel på ett kommersiellt producerat nätverk, erhållet på detta sätt, visas nedan. Denna utjämnare kunde korrigera för förlusterna i olika längder av koaxialkabel typ BICC T3205 (en kommersiell högkvalitativ 75Ω videokabel). Equalizern var en bryggad T-krets, snarare än ett gitter, vilket var lämpligt för koaxialkabel. Två versioner av kretsen tillverkades, en för kabellängder på 0 till 100 fot och den andra för kabellängder på 100 till 180 fot. Motstånd R ₁₇ och R ₁₈ "justerades vid test" (med R ₁₇ × R ₁₈ = 75 ² ) för att ge optimala resultat för en given kabellängd.

Iterativa procedurer genom datorprogrammering

Med tillkomsten av moderna datorer kan komplexa iterativa rutiner köras, som tidigare var oöverkomligt tidskrävande. Rutiner är möjliga som minimerar skillnaderna mellan en ungefärlig testlösning och målspecifikationen, antingen i "minsta kvadrater" eller "Chebyshev" mening. Programmen använder iterativa procedurer för att successivt lösa linjära programmeringsproblem, härledda lokalt, som ett sätt att hantera icke-linjära problem.

Ett exempel

Ett exempel som illustrerar metoden, betraktat som insättningsförlustkarakteristiken som visas i "Attenuation Plot" nedan.

Dämpningsdiagram för iterativ metod

Equalizer för att korrigera dämpningsdiagram

En kaskad av tre gittersektioner, som visas, valdes för att uppnå det erforderliga utjämnarsvaret.

Komponentvärdena, härledda genom iterationsproceduren, gav ett svar som matchade egenskapen i Chebyshev-bemärkelse, efter behov. Slutresultatet matchade målsvaret vid nio frekvenser (det finns nio frihetsgrader i kretsen R1 till R3, C1 till C3 och L1 till L3) med topp till toppfel på endast ± 0,03 dB vid mellanliggande frekvenser.

Restamplitudfel

Variabel utjämnare

I fallet med variabla utjämnare som endast ställs in genom att variera resistorvärden, är det vanligt att endast använda Bridged-T-nätverk eftersom det finns färre komponenter att matcha än i ett gitter. Även då, för att säkerställa ett helt matchat nätverk, är dubbla potentiometrar nödvändiga. Variabla utjämnare diskuteras också av Rounds et al. och Bode. Bode var intresserad av variabla utjämnare justerade med en enda potentiometer, så hans variabla utjämnare var inte konstanta motståndsnätverk.

Fasutjämnare

Introduktion

En fasutjämnare är en krets som kaskadkopplas med ett nätverk för att göra det övergripande fassvaret mer linjärt (eller för att göra gruppfördröjningen mer konstant). Den kombinerade kretsen kommer att sända vågformer med förbättrad trohet, jämfört med prestandan för det ursprungliga nätverket enbart.

Fasutjämning är ofta nödvändig eftersom många kretsar är utformade för att uppnå vissa dämpningsegenskaper, med liten hänsyn till den faskaraktäristik som uppstår. Detta är ofta fallet med filter till exempel, där, i strävan efter ett specifikt selektivitetskrav, ringa uppmärksamhet ägnas åt fassvaret hos det resulterande nätverket (som med Cauers filterdesignprocedur). Vanligtvis är kretsen som produceras ett minimifasnätverk , där plötsliga förändringar i amplitudsvaret alltid resulterar i olinjäriteter i fassvaret, på grund av det exakta förhållandet mellan amplitud och fas. Exempelvis kommer ett skarpt avskuret minimumfas-lågpassfilter med snabb övergång från passband till stoppband alltid att ha en faskarakteristik som avviker kraftigt från linjär vid frekvenser i närheten av gränsfrekvensen. Ju skarpare övergången är, desto större blir denna avvikelse. (Ett diagram av gruppfördröjningen kommer också att visa en stor ökning av fördröjningen i samma frekvensområde).

På liknande sätt kommer varje amplitudrippel i filterpassbandet också att åtföljas av rippel av faskarakteristiken. I många fall är både amplitud- och fasrippel oönskade och därför är det ingen mening att korrigera för en typ av rippel utan att också ta itu med den andra

Om vågformstrohet är viktigt är icke-linjära fasegenskaper oönskade. I exempelvis TV är de bildmässiga defekterna som kan tillskrivas fasförvrängning överdriven ringning av luminansinformationen och utsmetade och falska färgkanter vid övergångar i färginformationen.

I praktiken är faskorrigeringsprocedurer mest framgångsrika när de tillämpas på bandbegränsade system, såsom de som innehåller ett lågpass- eller bandpassfilter. Detta beror på att sådana filter i sig definierar ett ändligt frekvensband över vilket det är nödvändigt att tillämpa korrigeringen.

Såsom visas i gitternätverket är gitterallpasskretsen lämplig som ett faskorrigeringsnätverk eftersom den kan modifiera fasegenskaperna hos ett filternätverk utan att införa ändringar i dess amplitudsvar. Den konstanta resistansegenskapen betyder också att den inte skapar falska reflektioner på grund av felmatchningseffekter, när den kaskadkopplas med andra nätverk.

Ett exempel

Som ett exempel på faskorrigeringsprocessen, betrakta ett konventionellt Butterworth lågpassfilter av 9:e ordningen. Kretsen, som visas nedan, är det normaliserade filtret, som ska avslutas med 1 ohm och med enhetsgränsfrekvens).

Butterworth-filter av nionde ordningen

Amplituden och fasegenskaperna för detta filter anges i figurerna nedan. I den vänstra kurvan visas också fasfelskurvan för filtret (dvs faslutningens avvikelse från linjär). Som kan ses i den högra kurvan är enbart lågpassfiltrets faslutning linjär vid låga frekvenser men ökar för snabbt vid högre frekvenser, vilket slutligen resulterar i en fasavvikelse, från linjär, på 100 grader nära toppen av passbandet.

Amplitudsvar och fasfelsdiagram

Fassvar

Faskorrektor för LP-filter med n=9

För att korrigera för denna fasavvikelse behöver faskorrigeraren en linjär faskarakteristik vid låga frekvenser, men för att vara positiv till den linjära asymptoten när frekvensen ökar. En kaskad av tre andra ordningens all-pass gitter ger den erforderliga faskarakteristiken för filtret, och deras fassvar visas i den högra kurvan. I det här exemplet, eftersom filtret har en obalanserad form, är det nödvändigt att använda överbryggade T-ekvivalenter i faskorrigeraren, snarare än gitterkretsar. Faskorrigeraren visas nedan. Eftersom faskorrigeraren är en all-pass och konstant resistanskrets, ändrar den inte filtrets amplitudsvar.

Den kombinerade karakteristiken har en faskurva som är linjär över filtrets passband, men den resulterande höga faslutningen innebär att kombinationen har en betydligt större överföringsfördröjning än filtret ensamt.

I det här exemplet har Butterworth lågpassfiltret nio poler, placerade med likvinklade intervall på en enhetshalvcirkel i den vänstra halvan av det komplexa frekvensplanet, och polerna och nollorna för var och en av de tre faskorrektorerna är ±0,866 ±0,5j.

Övergående svar

Filtrets transienta beteende när det utsätts för en stegvågform visas ovan. Den första kurvan är för filtret, ensam, utan faskorrigering och den andra kurvan visar prestandan efter korrigering. Som väntat förbättrar faskorrigeringen vågformssymmetri, minskar stigtiden på 10–90 % och halverar ungefär toppamplituden för överskjutningarna, men det har ökat fördröjningen.

En översikt över designmetoder för faskorrigerare

I praktiken har en mängd olika tekniker använts vid utformningen av faskorrigerare. Den enklaste metoden använder sig av trial and error-procedurer, med hjälp av en grundläggande förståelse av all-pass-fasegenskaper. Proceduren kan vara förvånansvärt framgångsrik eftersom det ofta räcker med en kaskad av ett fåtal faskorrigerare baserade på det maximalt fasplatta andra ordningens gittret

Ett liknande tillvägagångssätt, baserat på användningen av standardfastabeller för utjämnare med parabolisk fördröjning, tillåter konstruktören att bestämma lämpligt nätverk för att möta en given toppfördröjning

En förbättrad procedur som noterar att gruppfördröjningsegenskaper för många nätverk kan betraktas som summor av paraboliska och linjära bidrag, använda diagram och grafer i kombination med tre anpassningstekniker, nämligen 3-punktspassningen, lutningspassningen eller den "genomsnittliga" passningen , för att bestämma komponentvärden.

Brain beskrev faskorrigeringen av en kaskad av 16 vakuumrör sammankopplade av andra ordningens maximalt platta mellanstegsnätverk. Faskarakteristiken härleddes från mätningar av amplitudsvaret genom att använda förhållandet mellan amplitud och fas för minsta fasskiftningsnätverk. Faskorrigering åstadkoms av tre identiska andra ordningens faskorrigerare i form av bryggkopplade T-nätverk.

Fredendhall gav pol-nollmönstret och kretsschemat för en fyrsektionsfördröjningsutjämnare som han föreslog till FCC skulle användas i sändare för att kompensera för egenskaperna hos den "genomsnittliga" mottagaren.

Ett mer matematiskt tillvägagångssätt har beskrivits som börjar med att välja en grundläggande kaskad av faskorrigerare och sedan optimera deras egenskaper genom en enkel kurvanpassningsprocedur. En LPF för TV-användning designades med denna metod.

Ännu mer sofistikerat har en iterativ konvergensprocedur körts på en dator för att optimera en kaskad av faskorrigerande sektioner. Genom att ha tillräckligt många sektioner tillgängliga för att ge det lämpliga antalet frihetsgrader kan den önskade faskarakteristiken uppnås i Chebyshev-bemärkelse.

En annan optimeringsprocedur började med att först notera att fördröjningarna av första och andra ordningens allpasssektioner adderas linjärt. Så för en kaskad av M första ordningens och N andra ordningens nätverk, kunde ett bäst passande val av M och N hittas för att möta vilken given egenskap som helst inom acceptabla gränser, genom att använda en minimaxapproximationsprocedur. Processen fortsatte i två steg, det första var att hitta en approximation som sammanföll med den önskade fördröjningen på en specificerad uppsättning punkter. Det andra steget bestod av att störa dessa punkter i ett försök att hitta en lika krusningslösning. Genom att öka antalet sektioner, valda i början, kan topp-topp-rippelfelet göras så litet som krävs.

Szentirmai har gett ut ett datorstödt designpaket kallat "S/FILSYN" som är kapabelt till allmän syntes, inklusive kretsar för amplitud och fasutjämning realiserade som gitter- eller bryggkopplade-T-nätverk. Han har också granskat ett antal andra datorstödda designpaket

Se även