Kvittra

För annan användning, se Chirp (disambiguation) .

En linjär chirp-vågform; en sinusformad våg som ökar i frekvens linjärt över tiden

Ett chirp är en signal där frekvensen ökar ( upp-chirp ) eller minskar ( down-chirp ) med tiden. I vissa källor används termen chirp omväxlande med svepsignal . Det appliceras vanligen på ekolods- , radar- och lasersystem och till andra applikationer, såsom i spridningsspektrumkommunikation (se spritt spektrum av kvittra ). Denna signaltyp är biologiskt inspirerad och uppstår som ett fenomen på grund av dispersion (ett icke-linjärt beroende mellan frekvens och utbredningshastigheten för vågkomponenterna). Det kompenseras vanligtvis genom att använda ett matchat filter, som kan vara en del av utbredningskanalen. Beroende på det specifika prestationsmåttet finns det dock bättre tekniker både för radar och kommunikation. Sedan den användes i radar och rymd, har den även använts för kommunikationsstandarder. För bilradarapplikationer kallas det vanligtvis linjär frekvensmodulerad vågform (LFMW).

Vid användning av spridningsspektrum används ofta ytakustiska vågor (SAW) för att generera och demodulera de kvittrade signalerna. Inom optiken uppvisar ultrakorta laserpulser också chirp, som i optiska transmissionssystem interagerar med materialens dispersionsegenskaper, vilket ökar eller minskar den totala pulsspridningen när signalen fortplantar sig . Namnet är en hänvisning till fåglarnas kvittrande ljud; se fågelvokalisering .

Definitioner

De grundläggande definitionerna här översätts till de vanliga fysikstorheterna läge (fas), hastighet (vinkelhastighet), acceleration (kvantitet). Om en vågform definieras som:

$x(t)=\sin \left(\phi (t)\right)$

då definieras den momentana vinkelfrekvensen , ω , som fashastigheten som ges av den första derivatan av fasen, där den momentana ordinarie frekvensen, f , är dess normaliserade version:

$\omega (t)={\frac {d\phi (t)}{dt}},\ ,f(t)={\frac {\omega (t)}{2\pi }}$

Slutligen definieras den momentana vinkelfrekvensen , γ , till att vara andraderivatan av momentan fas eller förstaderivatan av momentan vinkelfrekvens, där den momentana vanliga chirpyheten , c , är dess normaliserade version:

$\gamma (t)={\ frac {d^{2}\phi (t)}{dt^{2}}}={\frac {d\omega (t)}{dt}},\;c(t)={\frac {\ gamma (t)}{2\pi }}={\frac {df}{dt}}$

Sålunda är chirpyness förändringshastigheten för den momentana frekvensen.

Typer

Linjär

Spektrogram av ett linjärt pip. Spektrogramdiagrammet visar den linjära förändringshastigheten i frekvens som en funktion av tiden, i detta fall från 0 till 7 kHz, som upprepas var 2,3:e sekund. Diagrammets intensitet är proportionell mot energiinnehållet i signalen vid den angivna frekvensen och tiden.

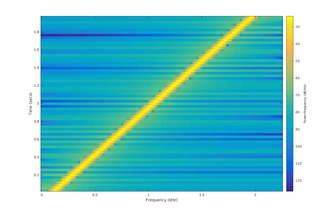
I en linjärfrekvent chirp eller helt enkelt linjär chirp varierar den momentana frekvensen ${\displaystyle f(t)} exakt linjärt med tiden:$

$f(t)=ct+f_{0}$ ,

där $f_{0}$ är startfrekvensen (vid tiden $t=0$ ) och $c$ är chirp-frekvensen, antagen konstant:

$c={\frac {f_{1}-f_{0}}{T}}$ .

Här är $f_{1}$ den slutliga frekvensen och $T$ är den tid det tar att svepa från $f_{0}$ till $f_{1}$ .

Den motsvarande tidsdomänfunktionen för fasen för varje oscillerande signal är integralen av frekvensfunktionen, eftersom man förväntar sig att fasen ska växa som ${\displaystyle \phi (t+\Delta t)\simeq \phi (t)+2\pi f(t)\,\Delta t} , dvs att fasens derivata är$ vinkelfrekvensen $\phi '(t)=2\pi \,f(t)$ .

För den linjära chirpen resulterar detta i:

${\begin{aligned}\phi (t)&=\phi _{0}+2\pi \int _{0}^{t}f(\tau )\,d\tau \\&=\phi _ {0}+2\pi \int _{0}^{t}\left(c\tau +f_{0}\right)\,d\tau \\&=\phi _{0}+2\pi \left({\frac {c}{2}}t^{2}+f_{0}t\right),\end{aligned}}$

där $\phi _{0}$ är den initiala fasen (vid tiden ${\displaystyle t=0} )$ . Detta kallas alltså också en kvadratisk fassignal .

Den motsvarande tidsdomänfunktionen för en sinusformad linjär chirp är sinus för fasen i radianer:

$x(t)=\sin \left[\phi _{0}+2\pi \left({\ frac {c}{2}}t^{2}+f_{0}t\right)\right]$

Exponentiell

En exponentiell chirp-vågform; en sinusformad våg som ökar i frekvens exponentiellt över tiden

Spektrogram av ett exponentiellt pip. Den exponentiella hastigheten för ändring av frekvens visas som en funktion av tiden, i detta fall från nästan 0 upp till 8 kHz som upprepas varje sekund. Också synligt i detta spektrogram är en frekvensfallback till 6 kHz efter topp, troligen en artefakt av den specifika metod som används för att generera vågformen.

I ett geometriskt chirp , även kallat ett exponentiellt chirp , varierar signalens frekvens med ett geometriskt förhållande över tiden. Med andra ord, om två punkter i vågformen väljs, $t_{1}$ och $t_{2}$ och tidsintervallet mellan dem $t_ {2}-t_{1}$ hålls konstant, frekvensförhållandet $f\left(t_{2}\right)/f\left(t_{1} \right)$ kommer också att vara konstant.

I ett exponentiellt chirp varierar signalens frekvens exponentiellt som en funktion av tiden:

$f(t)=f_{0}k^{t}$

där $f_{0}$ är startfrekvensen (vid $t=0$ ), och $k$ är hastigheten för exponentiell förändring i frekvens. Till skillnad från det linjära chirp, som har en konstant chirpyness, har ett exponentiellt chirp en exponentiellt ökande frekvens.

$k=\left({\frac {f_{1}}{f_{0}}}\right)^{\frac {1}{T}}$

Den motsvarande tidsdomänfunktionen för fasen av ett exponentiellt chirp är integralen av frekvensen:

${ \begin{aligned}\phi (t)&=\phi _{0}+2\pi \int _{0}^{t}f(\tau )\,d\tau \\&=\phi _{ 0}+2\pi f_{0}\int _{0}^{t}k^{\tau }d\tau \\&=\phi _{0}+2\pi f_{0}\left( {\frac {k^{t}-1}{\ln(k)}}\right)\end{aligned}}$

där $\phi _{0}$ är den initiala fasen (vid ${\displaystyle t=0} )$ .

Den motsvarande tidsdomänfunktionen för en sinusformad exponentiell chirp är sinus för fasen i radianer:

$x(t)=\sin \left[\phi _{0}+2\pi f_{ 0}\left({\frac {k^{t}-1}{\ln(k)}}\right)\right]$

Som var fallet för det linjära chirpet, består den momentana frekvensen för det exponentiella chirpet av grundfrekvensen $f(t)=f_{0}k^{t}$ åtföljd av ytterligare övertoner .

Hyperbolisk

Hyperboliska pip används i radartillämpningar, eftersom de visar maximalt matchat filtersvar efter att ha förvrängts av dopplereffekten.

I ett hyperboliskt pip varierar signalens frekvens hyperboliskt som en funktion av tiden:

$f(t)={\frac {f_{0}f_{1}T}{(f_{0}-f_ {1})t+f_{1}T}}$

Den motsvarande tidsdomänfunktionen för fasen av ett hyperboliskt pip är integralen av frekvensen:

${\ start{aligned}\phi (t)&=\phi _{0}+2\pi \int _{0}^{t}f(\tau )\,d\tau \\&=\phi _{0 }+2\pi {\frac {-f_{0}f_{1}T}{f_{1}-f_{0}}}\ln \left(1-{\frac {f_{1}-f_{ 0}}{f_{1}T}}t\right)\end{aligned}}$

där $\phi _{0}$ är den initiala fasen (vid ${\displaystyle t=0} )$ .

Den motsvarande tidsdomänfunktionen för en sinusformad hyperbolsk chirp är sinus för fasen i radianer:

$x(t)=\sin \left[\ phi _{0}+2\pi {\frac {-f_{0}f_{1}T}{f_{1}-f_{0}}}\ln \left(1-{\frac {f_{1 }-f_{0}}{f_{1}T}}t\right)\right]$

Generation

En chirp-signal kan genereras med analoga kretsar via en spänningsstyrd oscillator (VCO) och en linjärt eller exponentiellt rampande styrspänning . Den kan också genereras digitalt av en digital signalprocessor (DSP) och digital-till-analog-omvandlare (DAC), med hjälp av en direkt digital synthesizer (DDS) och genom att variera steget i den numeriskt styrda oscillatorn. Den kan också genereras av en YIG-oscillator .

Relation till en impulssignal

Chirp- och impulssignaler och deras (utvalda) spektrala komponenter . På botten ges fyra monokromatiska komponenter, sinusvågor med olika frekvens. Den röda linjen i vågorna ger den relativa fasförskjutningen till de andra sinusvågorna, som härrör från chirp-karakteristiken. Animeringen tar bort fasförskjutningen steg för steg (som med matchad filtrering ), vilket resulterar i en sinc-puls när ingen relativ fasförskjutning finns kvar.

En chirp-signal delar samma spektrala innehåll med en impulssignal . Emellertid, till skillnad från i impulssignalen, har spektrala komponenter i chirpsignalen olika faser, dvs deras effektspektra är lika men fasspektra är distinkta. Spridning av ett signalutbredningsmedium kan resultera i oavsiktlig omvandling av impulssignaler till pip. Å andra sidan använder många praktiska tillämpningar, såsom chirped pulsförstärkare eller ekolokaliseringssystem, chirp-signaler istället för impulser på grund av deras i sig lägre topp-till-medeleffektförhållande (PAPR).

Användningar och händelser

Chirp modulering

Chirp-modulering, eller linjär frekvensmodulering för digital kommunikation, patenterades av Sidney Darlington 1954 med betydande senare arbete utfört av Winkler 1962. Denna typ av modulering använder sinusformade vågformer vars momentana frekvens ökar eller minskar linjärt över tiden. Dessa vågformer kallas vanligtvis linjära chirps eller helt enkelt chirps.

Därför kallas hastigheten med vilken deras frekvens ändras för chirp-frekvensen . Vid binär chirpmodulering överförs binär data genom att bitarna avbildas till chirp med motsatta chirphastigheter. Till exempel, över en bitperiod tilldelas "1" ett chirp med positiv takt a och "0" ett chirp med negativ takt −a . Chirps har använts flitigt i radartillämpningar och som ett resultat finns avancerade källor för överföring och matchade filter för mottagning av linjära chirps tillgängliga.

(a) Vid bildbehandling förekommer sällan direkt periodicitet, utan snarare påträffas periodicitet-i-perspektiv. (b) Upprepande strukturer som det alternerande mörka utrymmet innanför fönstren och ljust utrymme i den vita betongen, "kvitter" (ökning i frekvens) åt höger. (c) Sålunda är det pip som passar bäst för bildbehandling ofta ett projektivt pip.

Chirplet transformation

Huvudartikel: Chirplet transform

En annan typ av pip är det projektiva pip, av formen:

$g=f\left[{\frac {a\cdot x+b}{c\cdot x+1}}\right]$ ,

med de tre parametrarna a (skala), b (översättning) och c (kvitter). Den projektiva chirpen är idealisk för bildbehandling och utgör grunden för den projektiva chirplet-transformen .

Nyckelkvitter

En förändring i morsekodens frekvens från den önskade frekvensen, på grund av dålig stabilitet i RF- oscillatorn , kallas chirp , och i RST-systemet ges en bifogad bokstav "C".

Se även

• Chirpspektrum - Analys av frekvensspektrumet för chirpsignaler
• Chirp compression - Ytterligare information om kompressionstekniker
• Chirp spridningsspektrum - En del av den trådlösa telekommunikationsstandarden IEEE 802.15.4a CSS
• Kvittrad spegel
• Chirped pulsförstärkning
• Chirplet-transform - En signalrepresentation baserad på en familj av lokaliserade chirp-funktioner.
• Radar med kontinuerliga vågor
• Dispersion (optik)
• Pulskompression
• Radioutbredning

externa länkar

• Online Chirp Tone Generator (WAV-filutgång)
• CHIRP ekolod på FishFinder
• CHIRP ekolod på FishFinder