Chirp spektrum

Spektrum för en chirp -puls beskriver dess egenskaper i termer av dess frekvenskomponenter. Denna frekvensdomänrepresentation är ett alternativ till den mer välbekanta tidsdomänvågformen, och de två versionerna är matematiskt relaterade av Fouriertransformen . Spektrumet är av särskilt intresse när pulser är föremål för signalbehandling . Till exempel, när en chirp-puls komprimeras av dess matchade filter innehåller den resulterande vågformen inte bara en smal huvudpuls utan också en mängd oönskade artefakter av vilka många är direkt hänförliga till egenskaper i chirpens spektrala egenskaper. Det enklaste sättet att härleda spektrumet av ett chirp, nu när datorer är allmänt tillgängliga, är att sampla tidsdomänvågformen vid en frekvens långt över Nyquist-gränsen och kalla fram en FFT -algoritm för att erhålla det önskade resultatet. Eftersom detta tillvägagångssätt inte var ett alternativ för de tidiga formgivarna, tillgrep de analytisk analys, där det var möjligt, eller till grafiska eller approximativa metoder, annars. Dessa tidiga metoder är fortfarande användbara, eftersom de ger ytterligare insikt i beteendet och egenskaperna hos kvitter.

Chirp puls

Ett allmänt uttryck för en oscillerande vågform, centrerad på frekvensen ω ₀ är

$s(t)=a(t)\cdot \exp[j(\omega _{0} \cdot t+\theta (t))]$

där $a(t)$ och θ (t) ger amplitud- och fasvariationerna för vågformen ${\displaystyle s} ,$ med tiden. Frekvensspektrumet för denna vågform erhålls genom att beräkna Fouriertransformen av s $\displaystyle s(t)} ,$ dvs.

$S(\omega )=\int _{-\infty }^{\infty }s(t)\cdot \exp(-j\omega t)\cdot dt=\int _{-\infty }^{\infty }a(t)\cdot \exp[j(\omega _{0}t+\theta (t))]\cdot \exp(-j\omega t )\cdot dt$ so $S(\omega ) =\int _{-\infty }^{\infty }a(t)\cdot \exp[j\left\{(\omega _{0}-\omega )\cdot t+\theta (t)\right\ }]\cdot dt$

I några speciella fall kan integralen lösas för att ge ett analytiskt uttryck , men ofta är egenskaperna hos $a(t)$ och θ (t) sådana att integralen endast kan utvärderas av en approximationsalgoritm eller genom numerisk integration .

Linjärt pip

I det speciella fallet där s(t) är begränsad till att vara en upp-chirp, platt toppad puls med dess momentana frekvens varierande som en linjär funktion av tiden, då är en analytisk lösning möjlig.

För enkelhetens skull anses pulsen ha enhetsamplitud och vara av varaktighet T, med amplituden och fasen definierade över tidsintervallet -T/2 till +T/2. Det totala frekvenssvepet är Δ F, varierande på ett linjärt sätt från - Δ F/2 till + Δ F/2 i det definierade tidsintervallet.

När frekvensen är en linjär funktion av tiden är fasen en kvadratisk funktion och s(t) kan skrivas

$s( )=1\cdot \exp[j(\Delta \Omega \cdot t+{\frac {\Delta \Omega }{2T}}\cdot t^{2})]\qquad {\text{där}}\quad \Delta \Omega =2\pi \cdot \Delta F\qquad {\text{and}}\quad {\frac {-T}{2}}<t<{\frac {T}{2}}$

Spektrum för denna linjära FM-signal är

$S(\omega )=\int _{-T/2}^{ T/2}\exp \left[j(\Delta \Omega \cdot t+{\frac {\Delta \Omega }{2T}}\cdot t^{2})\right]\cdot \exp(-j\ omega \cdot t)\cdot dt=\int _{-T/2}^{T/2}\exp \left[j\left\{(\Delta \Omega -\omega )\cdot t+{\frac { \Delta \Omega }{2T}}\cdot t^{2}\right\}\right]\cdot dt$

Genom att fylla i kvadraten och använda Fresnel-integralerna C(X) och S(X), definierade av

$C(X)=\int _{0}^ {X}\cos {\frac {\pi \cdot y^{2}}{2}}\cdot dy\qquad {\text{and}}\qquad S(X)=\int _{0}^{ X}\sin {\frac {\pi \cdot y^{2}}{2}}\cdot dy$

uttrycket kan utvärderas för att ge:

$S(\omega )={\sqrt {\left({\frac {\pi \cdot T}{\Delta \Omega }}\right) }}\cdot \exp \left[-j\left((\omega -\Delta \Omega )^{2}\cdot {\frac {T}{2\cdot \Delta \Omega }}\right)\right ]\cdot [C(X_{1})+j\cdot S(X_{1})+C(X_{2})+j\cdot S(X_{2})]$

där $X_{1}$ och $X_{2}$ ges av

$\quad X_{1}={ {{\frac {\Delta \Omega }{2}}+(\omega -\Delta \Omega )}{\sqrt {\frac {\pi \cdot \Delta \Omega }{T}}}}\quad { \text{och}}\quad X_{2}={\frac {{\frac {\Delta \Omega }{2}}+(\Delta \Omega -\omega )}{\sqrt {\frac {\pi \cdot \Delta \Omega }{T}}}}$

Det linjära FM-spektrumet kan anses ha tre huvudkomponenter, nämligen

• en amplitudterm, $|S(\omega )| ={\sqrt {\frac {\pi \cdot T}{\Delta \Omega }}}\cdot \left[\left(C(X_{1})+C(X_{2})\right)^{ 2}+\vänster(S(X_{1})+S(X_{2})\höger)^{2}\höger]^{\frac {1}{2}}$
• en kvadratisk lagfasterm, $\quad -\Phi _{1}(\omega )=(\omega -\Delta \ Omega )^{2}\cdot {\frac {T}{2\cdot \Delta \Omega }}$
• och en återstående fasterm $\quad \Phi _{2}(\ omega )=\arctan \left[{\frac {S(X_{1})+S(X_{2})}{C(X_{1})+C(X_{2})}}\höger]$

Förhållandet $\left[{\frac {S(X_{1})+S(X_{2} )}{C(X_{1})+C(X_{2})}}\höger]$ är ungefär enhet över en stor del av frekvensområdet av intresse så Φ ₂ approximerar till en konstant fasvinkel π /4 där. Om en frekvensskalningsterm n introduceras, där $n=2\cdot {\frac {(\omega -\omega _{0})}{\Delta \Omega }}$ , då blir uttrycken för Fresnel-argumenten

$X_{1}={\frac {\sqrt {T\cdot \Delta F}}{\sqrt {2}}}\cdot (1+ n)$ och

$X_{2}={\frac {\sqrt {T\cdot \Delta F}}{\sqrt {2}}}\ cdot (1-n)$

Spektrana är nu funktioner för produkten T. Δ F, oberoende av några speciella värden på mittfrekvens och bandbredd. Denna produkt, T. Δ F, hänvisas ofta till som tids-bandbreddsprodukten av chirpen.

Tabeller över Fresnel-integralerna har publicerats, tillsammans med matematiska rutiner för att beräkna integralerna manuellt eller med hjälp av ett datorprogram. Dessutom har ett antal matematiska program, såsom Mathcad , MATLAB och Mathematica , inbyggda rutiner för att utvärdera integralerna, antingen som standardfunktioner eller i tilläggspaket.

Vissa diagram av effektspektrum |S( ω )| ² som en funktion av frekvensen visas för tidsbandbreddsprodukter på 25, 100, 250 och 1000. När produkten är liten är Fresnel-ripplarna mycket tydliga, men spektrumet tenderar att ha en mer rektangulär profil för större värden.

När det gäller plotten av restfas, Φ 2( ω ), tenderar profilerna att vara mycket lika över ett brett spektrum av tids-bandbreddsprodukter. Två exempel, för TxB = 100 och 250 visas nedan. De har en fasvinkel nära värdet π /4 inom chirpområdet $\omega _{0}\pm \Delta \Omega /2$ och de börjar bara förändras signifikant för frekvenser utanför detta intervall.

Följaktligen, för frekvenser inom svepområdet för chirpen, är det kvadratlagfastermen Φ 1( ω ) och dess gruppfördröjningsfunktion (= -d Φ 1/d( ω ) ) som är av störst intresse. Det finns en plot av gruppfördröjningen som visas nedan. Både denna funktion och fasen Φ1 ( ω ) är oberoende av värdet på tids-bandbreddsprodukten. Som förväntat är gruppfördröjningen en linjär funktion med en varaktighet T sekunder, över ett frekvenssvep på ΔΩ rads.

Restfastermen lägger endast till mindre störningar till denna karakteristik inom frekvensområdet $\Delta \Omega \pm \Delta \Omega /2$ . Vid frekvenser utanför detta område avviker Φ 2( ω ) snabbt från π /4, och därför kommer den totala fasen att avvika allvarligt från en kvadratisk lag där. Lyckligtvis är energiinnehållet i chirpspektrumet mycket litet vid dessa frekvenser (vilket visas i ett senare avsnitt).

Icke-linjära pip

När Frequency-Time-karakteristiken är icke-linjär är Fourier-integralen svår att utvärdera. I sådana fall är det möjligt att tillgripa en approximationsmetod såsom den stationära fasapproximationen , eller att använda numeriska metoder.

Via stationär fasmetod

Ofta (som i radartillämpningar) är a(t) en långsamt varierande funktion av tiden och fasen θ (t) är oscillerande och varierar snabbt över integrationsområdet. Med sådana vågformer kan den stationära fasapproximationen användas för att undersöka spektrumet. Metoden bygger på det faktum att de största bidragen till Fourier-integralen kommer från den region där fasförändringshastigheten är minimal, dvs.

${\frac {d}{dt}}[(\omega _{ 0}-\omega )t+\theta (t)]=0\qquad eller\qquad (\omega -\omega _{0})-\theta '(t)=0$

Om inte θ (t) ωs _är en konstant, kommer tidpunkten ts _vid vilken fasen är stationär att variera enligt den momentana frekvensen . Uttrycker skillnaden mellan ( ω _s - ω ₀ ).t och θ (t) som en Taylor-serie om tiden t _s , men kasserar alla utom de tre första termerna (varav den andra termen är noll, här), Fourier-integralen kan skrivas ungefär som

$S(\omega )\approxeq a(t_{s})\int _{t_{s}-\delta }^{t_{s}+\delta }\ exp \left[-j\left\{(\omega _{s}-\omega _{0})\cdot t-\theta (t_{s})-{\frac {\theta ''(t_{s} })}{2}}\cdot (t-t_{s})^{2}\right\}\right]\cdot dt$

I denna ekvation representerar t _s en konstant tidpunkt, så termer som enbart beror på t _s kan tas utanför integralen. Uttrycket förenklas till $S(\omega )\approxeq {\sqrt {2\pi }}\cdot {\frac {a (t_{s})}{\sqrt {|\theta ''(t)|}}}\cdot \exp \left[j\left\{(\omega _{0}-\omega _{s}) t+\theta (t_{s})+{\frac {\pi }{4}}\right\}\right]$ så $|S(\omega _{t})|^{2}\approxeq 2\pi \cdot {\frac {a^{2}(t)}{|\theta ''(t)|}}$

där ω _t används för att indikera frekvensvariabelns beroende av t. Detta är ett mycket användbart uttryck som kopplar, som det gör, spektrumprofilen till amplituden och fasegenskaperna för chirpen.

För att utföra den inversa processen, dvs för att hitta tidsdomänfunktionen s(t) givna frekvensdomändata, härleds den inversa Fouriertransformen.

$s(t)={\frac {1}{2\pi }}\int _{-\infty }^{\ infty }|S(\omega )|\cdot \exp[j(\Phi (\omega )+\omega \cdot t)]\cdot d\omega$

där Φ (x) är spektrumets fasfunktion. De stationära faspunkterna för denna integrand är belägna vid

$\Phi '(\omega )=-t$

och följdsambandet, ekvivalent med det som härleds för spektrumet, kan erhållas genom den stationära fasmetoden, och är

$a^{2}(t_{\omega })\approxeq {\frac {1}{2\pi }}\cdot {\frac {|S(\omega )|^{2}}{|\ Phi ''(\omega )|}}$

Stationär fasanalys ger i själva verket följande (ungefärliga) Fourier-parrelationer: $a(t)\cdot \exp[j\theta (t)]\approxeq {\frac {1}{2\pi }}\cdot \int _{-\infty }^{\infty }S(\omega )|\cdot \exp[j\{\Phi (\omega )+\omega \cdot t\}]\cdot d\ omega$ och $|S(\omega )|\c exp[j\Phi (\omega )]\approxeq \int _{-\infty }^{\infty }a(t)\cdot \exp[-j\{\omega t-\theta (t)\}] dt$

Följaktligen kan approximativa uttryck för a(t) och θ (t) erhållas när spektrumet, inklusive dess fasfunktion Φ ( ω ) ges, och på liknande sätt kan approximativa uttryck för |S( ω | och Φ ( ω ) ges. erhålls när signalegenskaperna anges. Flera exempel på proceduren ges i litteraturen

Även om sambanden bara är ungefärliga, förbättras deras noggrannhet när tidsbandbreddsprodukten ökar. I de fall där signalenveloppen och spektrummodulen definieras av jämnt varierande Gauss-funktion kommer en T. Δ F-produkt så låg som 15 att ge acceptabla resultat, men om både a(t) och |S( ω )| definieras av rektangulära funktioner, då måste produkten T. Δ F vara mycket större, vanligtvis över 100.

Exempel

Typiskt, i radarfallet, är a(t) en konstant över signalens varaktighet och, för enkelhets skull, antas här vara enhet. Så fas- och amplitudegenskaperna, i frekvensdomänen, är relaterade till

$\Phi ''(\omega )=\pm {\frac {1}{2\pi }}\cdot |S(\omega )|^{2}$

Det finns två lösningar för Φ ( ω ), som är komplexa konjugat av varandra. De två filtren med dessa egenskaper kan användas som sändar- och mottagarfilter i ett radarsystem och är utbytbara. Gruppfördröjningskarakteristiken D( ω ), (där D( ω )=-d Φ /d ω ) , är

$D(\omega )=-\Phi '(\omega )=-\int _{0} ^{\infty }\Phi ''(\omega )\cdot d\omega +K$ så $D(\omega )=\pm {\frac {1}{2\pi }}\cdot \int _{0}^{\infty }|S(\omega )|^ {2}\cdot d\omega +K$

Så i fallet med en rektangulär tidsenvelopp, ges den dispersiva fördröjningskarakteristiken av integralen av kvadraten på enveloppen. Om det positiva tecknet tas, ökar gruppfördröjningen med ökande frekvens och vice versa. Resultatet är endast ungefärligt, men är mer exakt för stora värden av tidsbandbreddsprodukten. Betrakta, som ett exempel, fallet med ett spektrum som är enhetligt över intervallet - ω _max /2 till ω _max /2, sedan

$|S(\omega )|^{2}=A\qquad för\qquad |\omega |<{\frac {\omega _{max}}{2}}$ så $D(\omega )={\frac {1}{2\pi }}\cdot \int A\ cdot d\omega +K={\frac {A}{2\pi }}\cdot \omega +K$

Sätt D(- ω _max /2) = 0 och D( ω _max /2) = T, där T är pulslängden, sedan K = T/2 och A = (2 π T)/ ω _max så, slutligen $D(\omega )=T\cdot \left[{\frac {1}{2}}+{\frac {\omega }{ \omega _{max}}}\right]$

Som förväntat motsvarar ett platt toppat frekvensspektrum ett linjärt frekvenssvep.

Det linjära kvittret är bara ett specialfall som i alla fall kan beräknas mer exakt med metoderna i det tidigare avsnittet. Den speciella användbarheten av den stationära fasmetoden ligger i dess förmåga att ge resultat när frekvenssvepet är icke-linjärt. I sådana fall kan det spektrala svaret formas för att uppfylla vissa önskade designkriterier, till exempel låga sidolober när ett pip komprimeras. En sådan familj av spektrala funktioner som har studerats ges av

$|S(\omega )|^{2}=A_{n}\cdot cos^{n}\left( {\frac {\pi \omega }{\omega _{max}}}\right)\qquad där\qquad |\omega |<{\frac {\omega _{max}}{2}}\qquad och\ n\ är\ ett\ heltal$

Det är möjligt att hitta gruppfördröjningsegenskaperna för dessa funktioner på ett liknande sätt som utförts ovan och resultaten för n = 1 till 4 har beräknats. Även om dessa cosinusfunktioner är mottagliga för matematisk manipulation, väljs de sällan för att definiera de spektrala egenskaperna hos en chirp, i praktiken, eftersom de när de komprimeras ger breda huvudpulser med höga sidolobsnivåer. En bättre egenskap (bland många) är Hamming-funktionen, som ges av

$(\displaystyle | omega )|^{2}=A\cdot \left[0.54+0.46\cdot cos\left({\frac {2\pi \omega }{\omega _{max}}}\right)\right]=A \cdot \left[0.08+0.92\cdot cos^{2}\left({\frac {\pi \omega }{\omega _{max}}}\right)\right]}$

En plot av denna egenskap visas, plottad över området - ω _max /2 till ω _max /2.

Genom att tillämpa de ovan angivna ekvationerna kan gruppfördröjningskarakteristiken som uppnår denna spektrala form erhållas. Det är

$D_{H}(\omega )=T\cdot \left[{\frac {1}{2}}+{\frac {\omega }{\omega _{max}}}+{\frac {1.7037}{4\pi }}\cdot sin\left({ \frac {2\pi \omega }{\omega _{max}}}\right)\right]$

Eftersom principen om stationär fas visar att det finns ett direkt samband mellan förfluten tid och den momentana signalfördröjningen, kan t/T för Hamming-fönstret relateras till ω / ω _max med

${\frac {t}{T}}={\frac {1}{2 }}+{\frac {\omega }{\omega _{max}}}+{\frac {1.7037}{4\pi }}\cdot sin\left({\frac {2\pi \omega }{\ omega _{max}}}\right)$

Denna egenskap som är tid som funktion av frekvens visas här. Att invertera plottet ger den vanligare (och mer användbara) plotten av frekvens som en funktion av tiden, vilket också visas.

Andra spektrala former kan undersökas på samma sätt och resultaten, även om de är ungefärliga, är förvånansvärt exakta, speciellt när pulsens tidsbandbreddsprodukt är hög.

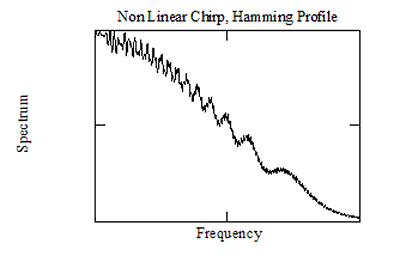
Den stationära fasmetoden förutsäger eller hanterar inte Fresnell-rippels, så den kan inte erbjuda något sätt med vilket dessa rippel kan minimeras. Som ett exempel visar figuren nedan ett chirp-spektrum med T. Δ F =250 erhållet för ett icke-linjärt chirp som syftar till att matcha Hamming-fönstret, med de metoder som beskrivs ovan. Figuren visar att den spektrala profilen matchar Hamming-karaktäristiken ganska bra, men Fresnell-ripplar, som inte förutspås av metoden, är mycket tydliga.

Via numeriska metoder

Provtagning

Närhelst en Fourierintegral inte kan utvärderas med analytiska medel är en ungefärlig lösning vanligtvis möjlig genom numerisk analys . En sådan procedur kräver att funktionen samplas, vanligtvis med jämna mellanrum i tiden. En konsekvens av sampling är att det resulterande spektrumet är periodiskt i frekvensdomänen. Förutom det (önskade) basbandsspektrumet förekommer ytterligare versioner av spektrumet, centrerade på multiplar av samplingsfrekvensen. För att säkerställa att det inte finns någon överlappning av frekvensdata (dvs ingen aliasing) måste Nyquists samplingssats vara uppfylld. I praktiken är en samplingsfrekvens som är betydligt högre än den som dikteras av samplingssatsen att rekommendera

Spektrum av en samplade signal - Fouriertransformen av en diskret tidssignal

Ett enkelt sätt att approximera en integral, till exempel en Fourier-integral, är att använda standarden " rektangelregel" för numerisk integration. Metoden antar att signalvärdet taget vid ett sampelögonblick förblir konstant under ett samplingsintervall, tills nästa prov tas. Denna procedur kallas ibland för en "lådbilsgenerator", eller ett nollordsprov och håll. Om tidsintervallet mellan sampel är W, då är s _n = s(nW), och den önskade integralen erhålls ungefär genom att summera de rektangulära ytorna. Det så erhållna resultatet är faltningen av en rektangulär puls med stegstorlek W med impulserna lokaliserade vid samplingsögonblicken med vikter lika med sampelvärdena. Följaktligen kommer det intressanta spektrumet att ha överlagrat frekvenssvaret för samplet och hållet, och spektrumet för den samplade signalen Ss ges av:

$Ss(\omega )) =W{\frac {\sin(\omega W/2)}{\omega W/2}}\cdot \left[\sum _{n=-\infty }^{\infty }s_{n}\cdot \exp(-jn\omega W)\right]$

Den första delen av uttrycket, dvs 'sin(x)/x'-delen, är frekvenssvaret för samplet och hållet. Dess amplitud minskar med frekvensen och den faller till 63 % av dess toppvärde vid halva samplingsfrekvensen och den är noll vid multiplar av den frekvensen (eftersom f s = ₁ /W). Den andra termen i ekvationen kallas Fouriertransformen av den diskreta signalen s _n . Det är en kontinuerlig funktion över alla ω och involverar ett oändligt antal summeringar. I praktiken kan summeringsprocessen trunkeras till ett ändligt antal sampel, N, möjligen på grund av att vågformen är periodisk eller noll utanför sampelområdet. Dessutom, eftersom samma spektrum upprepas oändligt, är det möjligt att begränsa intresset till spektraldata inom området - ω _s /2 till + ω _s /2.

Som ett exempel samplas ett exponentiellt chirp (med dess toppfrekvens långt under Nyquist-gränsen) vid 256 punkter, som visas.

Det samplade spektrumet, Ss( ω ) för denna vågform, beräknat med hjälp av ekvationen ovan, visas. För att förenkla plotten har endast resultaten vid positiva frekvenser visats. Inverkan av frekvensspektrumet för nollordningens hållkrets framgår tydligt i diagrammet.

Basbandsdelen av spektrumet visas mer detaljerat i nästa figur och svaret visar en distinkt lutning, som är betydligt lägre vid de högre frekvenserna.

Även om karaktäristiken för nollordningens hållning har en liten inverkan på detta resultat, beror lutningen främst på egenskaperna hos chirpen. Vågformen sveper relativt snabbt över de höga frekvenserna och lägger mer tid på att svepa de låga frekvenserna, följaktligen blir det mindre energiinnehåll vid de höga frekvenserna med mer vid de lägre. (En linjär chirp, å andra sidan, har ett nominellt platt spektrum eftersom dess frekvenser svepas med samma hastighet, som visas i några tidigare diagram).

Via den diskreta Fouriertransformen

Om vi ​​begränsar intresset för utgångsspektrumet till ett ändligt antal diskreta datapunkter (= N), vid frekvenser ω _m som ges av $\omega _{m}={\frac {2\pi m}{NW}}\qquad för\qquad m=0,1,2,...N-1$

är formeln för att beräkna den diskreta Fouriertransformen

$Ss_{m}\quad =Ss\left (j{\frac {2\pi m}{NW}}\right)\quad =\quad \sum _{n=0}^{N-1}s_{n}\cdot exp(-j\left( {\frac {2\pi mn}{N}}\right)$

Beräkningarna kan utföras med hjälp av en enkel datoralgoritm, men detta är inte särskilt effektivt vid datoranvändning. Följaktligen har effektivare algoritmer utvecklats, särskilt Fast Fourier Transforms (FFT). Datorprogram som implementerar FFT är allmänt tillgängliga i litteraturen och i proprietära CAD-program som Mathcad , MATLAB och Mathematica . I följande exempel samplas en linjär chirp med tidsbandbreddsprodukten 25 vid 128 punkter (dvs N = 128). I figuren visas prover av den verkliga delen av vågformen - observera att dessa är prover i tidsdomänen. FFT-processen antar att vågformen är cyklisk, så dessa 128 datapunkter kan anses vara en del av en oändligt upprepad sekvens i tiden.

Genom att beräkna N-punkts FFT för dessa data erhålls det diskreta spektrumet för sekvensen. Storleken på detta spektrum visas i den bifogade bilden, där dessa datapunkter är prover i frekvens. Uppgifterna är cykliska så i diagrammet är nollfrekvenspunkten vid n = 0 och även vid n = 128 (dvs båda punkterna har samma frekvens). Punkten n = 64 motsvarar +fs/2 (och även -fs/2).

För att visa spektrumet mer detaljerat (men inte nödvändigtvis med mer upplösning) kan tidssekvensen utökas med nollutfyllnad. Till exempel, förlängning av tidssekvensen på 128 punkter med nollor för att ge N = 4096 resulterar i att den del av spektrumet som ursprungligen presenterades i 16 sampel, nu presenteras i 512 sampel, som visas.

Spektral spridning

Det finns väldigt lite spektralt innehåll bortom svepfrekvensområdet för en chirp-puls och detta gäller särskilt för vågformer där tids-bandbreddsprodukten är stor. Hela linjen på grafen i den intilliggande figuren visar resultat för linjära pip. Den visar till exempel att endast cirka 2 % av den totala effekten finns vid frekvenser utanför svepområdet Δ F när tidsbandbredden är 100, och den är mindre än 1/2 % när T. Δ F är 500. I fallet med en icke-linjär chirp, eller en linjär chirp formad av amplitudviktning, är andelen effekt utanför Δ F ännu lägre, som visas på grafen, där den streckade linjen är för spektra med Hamming-profiler. Denna låga spektrala spridning är särskilt signifikant när basbandssignaler ska digitaliseras eftersom den tillåter att en samplingsfrekvens kan väljas som endast är något högre än två gånger den maximala frekvensavvikelsen för chirpen.

Reducerar spektral krusning

Fresnel-ripplarna på ett chirp-spektrum är mycket påträngande, speciellt när tidsbandbreddsprodukterna är låga (under 50, låt oss säga) och deras närvaro leder till höga tidssidolobsnivåer när chirps utsätts för pulskompression som i radar- och sonarsystem . De uppstår på grund av de plötsliga diskontinuiteterna i chirp-vågformen vid början och avslutningen av pulsen. Även om det finns ett antal procedurer som kan tillämpas för att minska krusningsnivåerna, är de inte alla lika effektiva. Vidare kräver vissa av metoderna amplitudformning, eller amplitudmodulering, av chirppulsen och detta gör dessa metoder olämpliga när till exempel chirppulserna ska sändas av en effektförstärkare som arbetar i ett närabegränsande tillstånd. För sådana system är endast metoderna som använder frekvens (eller fas) fördistorsion lämpliga.

Introduktion av stig- och falltider med ändlig varaktighet

Om övergångarna i början och slutet av chirpen görs mindre plötsliga (eller mer "rundade"), så uppnås en minskning av rippelamplituden. Varaktigheterna för de två övergångsområdena behöver bara vara en liten bråkdel av pulslängden, och föreslagna värden är mellan 2/ Δ F och 3/ Δ F men, som förväntat, när pulsens tidsbandbreddsprodukt är liten, längre övergångsperioder behövs. De faktiska profilerna för dessa stig- och fallområden av en puls verkar inte vara kritiska och kan tillhandahållas till exempel av bandbegränsande filter i analoga implementeringar och en linjär lutning i digitala. Två exempel visar spektra av linjära pip med ändliga stigtider. Den första är för ett chirp med en tidsbandbredd på 250, där stig- och falltiderna är 4 % av den totala pulslängden och den andra är för ett chirp med en tidsbandbredd på 25, där stig- och falltiderna är 10 % av totalen. Dessa två spektra visar en markant minskning av krusningsamplituden jämfört med spektra av omodifierade linjära chirps som visats tidigare.

Applicera fas- eller frekvensdistorsion på chirp-pulsen

En analog teknik kan appliceras på frekvenskarakteristiken för chirp-vågformen genom att lägga till linjära FM-distorsionssegment (kvadratisk fasmodulationsdistorsion) till chirpens frekvenskarakteristika, såsom visas. Metoden är effektiv eftersom amplitud- och fasförvrängningar med funktionell likhet kan ge liknande effekter när distorsionsfaktorerna är små.

Föreslagna värden för dessa distorsionsregioner för att ge bra resultat är: $\Delta f_{p}=0,75\Delta F\qquad och\qquad \delta =1/\Delta F$

Senare arbete föreslog något olika värden, nämligen: $\Delta f_{p}=0,73\Delta F\qquad och\qquad \delta =0,86/\ Delta F$ men resultatet kan utan tvekan förbättras genom att optimera värden för varje enskild situation. Två diagram visar effekterna av frekvensförkorrigering och kan jämföras med resultaten i de tidigare avsnitten.

Den rippelreduktion som uppnås genom frekvensförkorrigering, även om den är signifikant, anses vara mindre framgångsrik än den som uppnåddes med amplitudmoduleringsmetoderna i föregående avsnitt. Det har dock föreslagits att genom att implementera kubisk (snarare än kvadratisk) fasförkorrigering kan jämförbara resultat uppnås.

Att härleda en vågform från ett målfrekvensspektrum

Denna metod använder en invers Fouriertransform för att härleda en vågform som har ett spektrum med faskarakteristiken för en vald chirp men en ny amplitudprofil som är rektangulär och rippelfri. Metoden är mycket effektiv, men tyvärr har vågformen som härleds en semi-oändlig varaktighet. Om, för enkelhets skull, den nyligen härledda vågformen trunkeras till en praktisk längd, så återinförs en viss rippel på spektrumet. Som ett exempel visas en linjär chirp-vågform med en tidsbandbredd på 25 tillsammans med dess spektrumstorlek (visas med en hel linje) som, som visats tidigare, har en stor rippelkomponent. Det är möjligt att med hjälp av en invers FFT hitta en chirp-vågform som i frekvensdomänen har samma faskarakteristik som tidigare, men med den rektangulära magnitudkarakteristik som visas av den streckade linjen på plotten. Den chirp-vågform som härrör från denna process har en mycket lång varaktighet, men när den är trunkerad för att säga en längd 2T, så får spektrumet någon rippel igen, som visas.

Använda fönsterfunktioner

Det finns många applikationer där ett spektrum med en rektangulär magnitudprofil inte är idealiskt. Till exempel, när en chirp-vågform komprimeras med hjälp av dess matchade filter, så närmar sig den resulterande vågformen sinc -funktionen och har följaktligen irriterande höga sidlober. Ofta, för att förbättra pulsens egenskaper och sänka sidolobsnivåerna, modifieras dess spektrum, vanligtvis till en klockformad profil. Liknande problem uppstår vid digital signalbehandling där spektralformningen tillhandahålls av en fönsterfunktion , en process som ibland kallas apodisering . I fallet med en antennuppsättning används liknande profilering genom "viktningsfunktioner" för att reducera de rumsliga sidoloberna i strålningsmönstret. Även om spektral formning av en chirp skulle kunna tillämpas i frekvensdomänen, erhålls bättre resultat om formningen utförs i tidsdomänen. Exempel på denna process visas för linjära chirps med tidsbandbreddsprodukter på 250 och 25. De har formats av ett 3-terms Blackman-Harris-fönster givet av $|U(\omega )|^{2}=3-0,4.cos vänster({\frac {2\pi \omega }{\omega _{max}}}\right)+0,07922\cos \left({\frac {4\pi \omega }{\omega _{max}}} \right)$ Spektra, nu klockformade, ses vara fria från krusningar.

Icke-linjära pip kan skapas som har ett klockformat spektrum, såsom Blackman-Harris-fönstret som just diskuterades, och som följaktligen kommer att uppvisa minskad rippel jämfört med det linjära pip. Med hjälp av den tidigare beskrivna stationära fasmetoden kan ett ungefärligt samband mellan tid och frekvens erhållas och är: ${\frac {t}{T}}={\frac {1}{2}}+{\frac {\omega }{\omega _{max}} }+0,1871\sin \left({\frac {2\pi \omega }{\omega _{max}}}\right)+0,014895\sin \left({\frac {4\pi \omega }{\omega _{max}}}\right)$

Genom att arrangera om ekvationen kan en plot av frekvens mot tid ritas, som visas.

Som exempel visas diagram över de spektrala magnituderna för icke-linjära chirps med spektrala profiler för Blackman-Harris-fönster och med tidsbandbreddsprodukter på 250 och 25 nedan. Som man kan se finns det en viss rippelreduktion, men den nedslående prestandan kan tillskrivas det faktum att dessa pip, även om de har minskat energiinnehåll i sina yttre frekvensområden, har de fortfarande amplitudprofiler med snabba stig- och falltider.

Se även

• Pulskompression , en process som använder frekvens- eller faskodade vågformer för att förbättra signalen till bruset från mottagna signaler.
• Chirp compression , en kompressionsprocess endast för chirp.