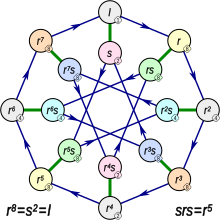
Kvasidihedrisk grupp

Cayley-graf av den kvasidihedriska gruppen av ordning 16

Cayley-graf för den modulära maximal-cykliska gruppen av ordning 16

Cayley-graf av den dihedriska gruppen av ordning 16

Inom matematiken är de kvasi-dihedriska grupperna , även kallade semi-dihedriska grupper , vissa icke-abelska grupper av ordning en potens av 2. För varje positivt heltal n större än eller lika med 4, finns det exakt fyra isomorfismklasser av icke- abelska grupper av ordningen 2 ⁿ som har en cyklisk undergrupp av index 2. Två är välkända, den generaliserade quaterniongruppen och den dihedriska gruppen . En av de återstående två grupperna anses ofta vara särskilt viktig, eftersom det är ett exempel på en 2-grupp med maximal nilpotensklass . I Bertram Hupperts text Endliche Gruppen kallas denna grupp för en "Quasidiedergruppe". I Daniel Gorensteins text, Finite Groups , kallas denna grupp för "semidihedral group". Dummit och Foote hänvisar till det som den "kvasidihedriska gruppen"; vi antar det namnet i den här artikeln. Alla ger samma presentation för denna grupp:

$\langle r,s\mid r^{2^{n-1}}= s^{2}=1,\ srs=r^{2^{n-2}-1}\rangle \,\!$ .

Den andra icke-abelska 2-gruppen med cyklisk undergrupp av index 2 ges inget speciellt namn i någon av texterna, utan hänvisas till som bara G eller M _m (2). När denna grupp har ordning 16, refererar Dummit och Foote till denna grupp som "modulgruppen av ordning 16", eftersom dess gitter av undergrupper är modulärt . I den här artikeln kommer denna grupp att kallas den modulära maximal-cykliska gruppen av ordningen $2^{n}$ . Dess presentation är:

$\langle r,s\mid r^{2^{n-1}}= s^{2}=1,\ srs=r^{2^{n-2}+1}\rangle \,\!$ .

Både dessa två grupper och den dihedriska gruppen är halvdirekta produkter av en cyklisk grupp < r > av ordningen 2 ^{n −1} med en cyklisk grupp < s > av ordningen 2. En sådan icke-abelsk halvdirekt produkt bestäms unikt av ett ordningselement 2 i gruppen av enheter i ringen $\mathbb {Z} /2^{n-1}\mathbb {Z}$ och det finns exakt tre sådana element, $2^{n-1}-1$ , $2^{n-2}-1$ och $2^{n -2}+1$ , motsvarande den dihedriska gruppen, den kvasidiedriska gruppen och den modulära maximalcykliska gruppen.

Den generaliserade kvaterniongruppen, den dihedriska gruppen och den kvasidihedriska gruppen av ordning 2 ⁿ har alla nilpotensklass n − 1 och är de enda isomorfismklasserna av grupper av ordningen 2 ⁿ med nilpotensklass n − 1. Grupperna av ordningen p ⁿ och nilpotensklass n − 1 var början på klassificeringen av alla p -grupper via coclass . Den modulära maximalcykliska gruppen av ordning 2 ⁿ har alltid nilpotensklass 2. Detta gör den modulära maximalcykliska gruppen mindre intressant, eftersom de flesta grupper av ordningen p ⁿ för stora n har nilpotensklass 2 och har visat sig vara svåra att förstå direkt.

Den generaliserade quaternion, den dihedral och den kvasidihedriska gruppen är de enda 2-grupperna vars härledda undergrupp har index 4. Alperin-Brauer-Gorenstein-satsen klassificerar de enkla grupperna , och till en viss grad de ändliga grupperna , med kvasidihedriska Sylow 2-undergrupper .

Exempel

Sylow 2-undergrupperna i följande grupper är kvasidihedriska:

• PSL ₃ ( F _q ) för q ≡ 3 mod 4,
• PSU ₃ ( F _q ) för q ≡ 1 mod 4,
• Mathieu -gruppen M ₁₁ ,
• GL ₂ ( F _q ) för q ≡ 3 mod 4.

•   Dummit, DS; Foote, R. (2004). Abstrakt Algebra (3 uppl.). Wiley. s. 71–72. ISBN 9780471433347 .
•   Huppert, B. (1967). Endliche Gruppen . Springer. s. 90–93. MR 0224703 .
•    Gorenstein, D. (1980). Finita grupper . Chelsea. s. 188–195. ISBN 0-8284-0301-5 . MR 0569209 .