Kvantitativa modeller av handlingspotentialen

Inom neurofysiologi har flera matematiska modeller av aktionspotentialen utvecklats, som delas in i två grundläggande typer. Den första typen syftar till att modellera experimentdata kvantitativt, dvs att återge mätningarna av ström och spänning exakt. Den berömda Hodgkin-Huxley-modellen av axonet från Loligo -bläckfisken exemplifierar sådana modeller. Även om det är kvalitativt korrekt beskriver HH-modellen inte varje typ av exciterbart membran exakt, eftersom den endast beaktar två joner (natrium och kalium), var och en med bara en typ av spänningskänslig kanal. Andra joner som kalcium kan dock vara viktiga och det finns en stor mångfald av kanaler för alla joner. Som ett exempel hjärtaktionspotentialen hur olika formade aktionspotentialer kan genereras på membran med spänningskänsliga kalciumkanaler och olika typer av natrium/kaliumkanaler. Den andra typen av matematisk modell är en förenkling av den första typen; Målet är inte att reproducera experimentella data, utan att kvalitativt förstå aktionspotentialernas roll i neurala kretsar. För ett sådant syfte kan detaljerade fysiologiska modeller vara onödigt komplicerade och kan skymma "skogen för träden". FitzHugh -Nagumo-modellen är typisk för denna klass, som ofta studeras för sitt indragningsbeteende . Entrainment observeras vanligen i naturen, till exempel i synkroniserad tändning av eldflugor , som koordineras av en explosion av aktionspotentialer; indragning kan också observeras i individuella neuroner. Båda typerna av modeller kan användas för att förstå beteendet hos små biologiska neurala nätverk , såsom de centrala mönsterbildare som ansvarar för vissa automatiska reflexåtgärder. Sådana nätverk kan generera ett komplext tidsmönster av aktionspotentialer som används för att koordinera muskelsammandragningar, till exempel de som är involverade i andning eller snabb simning för att undkomma ett rovdjur.

Hodgkin-Huxley modell

Ekvivalent elektrisk krets för Hodgkin-Huxley-modellen av aktionspotentialen. Im och Vm representerar strömmen genom, respektive spänningen över _,_en liten membranfläck. Cm representerar kapacitansen för membranlappen, medan de fyra g: n representerar konduktanserna för fyra _typer av joner. De två konduktanserna till vänster, för kalium (K) och natrium (Na), visas med pilar för att indikera att de kan variera med den pålagda spänningen, motsvarande de spänningskänsliga jonkanalerna .

1952 utvecklade Alan Lloyd Hodgkin och Andrew Huxley en uppsättning ekvationer för att passa deras experimentella spänningsklämmadata på det axonala membranet. Modellen antar att membrankapacitansen C är konstant; således ändras transmembranspänningen V med _den totala transmembranströmmen Itot enligt ekvationen

C{\frac {dV}{dt}}=I_{\mathrm {tot} }=I_ {\mathrm {ext} }+I_{\mathrm {Na} }+I_{\mathrm {K} }+I_{\mathrm {L} }

där INa , Ik och IL är strömmar _som transporteras genom de lokala natriumkanalerna, kaliumkanalerna respektive "läckage"-kanalerna (en catch-all ₎_. Den initiala termen I _ext representerar strömmen som kommer från externa källor, såsom excitatoriska postsynaptiska potentialer från dendriterna eller en vetenskapsmans elektrod.

Modellen antar vidare att en given jonkanal antingen är helt öppen eller stängd; om den är stängd är dess konduktans noll, medan om den är öppen är dess konduktans ett konstant värde g . Nettoströmmen genom en jonkanal beror alltså på två variabler: sannolikheten p _öppen för att kanalen är öppen, och skillnaden i spänning från den jonens jämviktsspänning, V − V _eq . Till exempel kan strömmen genom kaliumkanalen skrivas som

I_{\mathrm {K} }=g_{\mathrm {K} }\left(V-E_{\mathrm {K} }\right)p_{\mathrm {öppen,K} }

vilket motsvarar Ohms lag . Per definition flyter ingen nettoström ( IK = 0) när transmembranspänningen är lika med jämviktsspänningen för den jonen (när V = E _K ) _.

För att passa sina data korrekt antog Hodgkin och Huxley att varje typ av jonkanal hade flera "portar", så att kanalen var öppen endast om alla portar var öppna och stängda annars. De antog också att sannolikheten för att en grind skulle vara öppen var oberoende av att de andra grindarna var öppna; detta antagande validerades senare för inaktiveringsporten. Hodgkin och Huxley modellerade den spänningskänsliga kaliumkanalen med fyra grindar; låter p _n beteckna sannolikheten för att en enda sådan grind är öppen, är sannolikheten för att hela kanalen är öppen produkten av fyra sådana sannolikheter, dvs p _{öppen, K} = n ⁴ . På liknande sätt modellerades sannolikheten för den spänningskänsliga natriumkanalen att ha tre liknande grindar med sannolikhet m och en fjärde grind, associerad med inaktivering, med sannolikhet h ; alltså, p _{öppen, Na} = m ³ h . Sannolikheterna för varje grind antas följa första ordningens kinetik

{\frac {dm}{dt}}=-{\frac {m-m_{\mathrm {eq} }}{\tau _{m} }}

där både jämviktsvärdet m _eq och relaxationstidskonstanten τ _m beror på den momentana spänningen V över membranet. Om V ändras på en tidsskala långsammare än τ _m , kommer m -sannolikheten alltid att vara ungefär lika med dess jämviktsvärde m _eq ; men om V ändras snabbare, kommer m att släpa efter m _ekv . Genom att anpassa sina spänningsklämmadata kunde Hodgkin och Huxley modellera hur dessa jämviktsvärden och tidskonstanter varierade med temperatur och transmembranspänning. Formlerna är komplexa och beror exponentiellt på spänningen och temperaturen. Till exempel varierar tidskonstanten för natriumkanalaktiveringssannolikhet h som 3 ^{(θ−6,3)/10} med Celsiustemperaturen θ och med spänningen V som

{\frac {1}{\tau _{h}}}=0.07e^{-V/20}+{\frac {1}{1+e^{3-V/10}}}.

Sammanfattningsvis är Hodgkin-Huxley-ekvationerna komplexa, icke-linjära vanliga differentialekvationer i fyra oberoende variabler : transmembranspänningen V och sannolikheterna m , h och n . Ingen generell lösning av dessa ekvationer har upptäckts. En mindre ambitiös men allmänt användbar metod för att studera sådana icke-linjära dynamiska system är att överväga deras beteende i närheten av en fast punkt . Denna analys visar att Hodgkin-Huxley-systemet genomgår en övergång från stabil vila till bristande svängningar när den stimulerande strömmen I _ext gradvis ökas; anmärkningsvärt nog blir axonen stabilt vilande igen när den stimulerande strömmen ökas ytterligare. En mer allmän studie av de typer av kvalitativa beteenden hos axoner som förutspåtts av Hodgkin-Huxley-ekvationerna har också utförts.

FitzHugh-Nagumo modell

Figur FHN: För att efterlikna aktionspotentialen använder FitzHugh–Nagumo-modellen och dess släktingar en funktion g ( V ) med negativt differentialmotstånd (en negativ lutning på I vs. V -diagrammet). Som jämförelse skulle ett normalt motstånd ha en positiv lutning, enligt Ohms lag I = GV , där konduktansen G är inversen av resistansen G =1/ R .

På grund av komplexiteten i Hodgkin-Huxley-ekvationerna har olika förenklingar utvecklats som uppvisar kvalitativt liknande beteende. FitzHugh –Nagumo-modellen är ett typiskt exempel på ett sådant förenklat system. Baserat på tunneldioden har FHN-modellen bara två oberoende variabler, men uppvisar ett liknande stabilitetsbeteende som de fullständiga Hodgkin-Huxley-ekvationerna. Ekvationerna är

C{\frac {dV}{dt}}=Ig(V),

L {\frac {dI}{dt}}=EV-RI

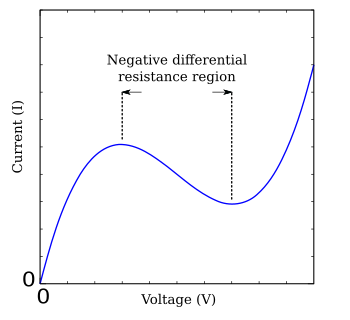
där g(V) är en funktion av spänningen V som har en region med negativ lutning i mitten, flankerad av ett maximum och ett minimum (Figur FHN). Ett mycket studerat enkelt fall av FitzHugh-Nagumo-modellen är Bonhoeffer-van der Pols nervmodell, som beskrivs av ekvationerna

C{\frac {dV}{dt}}=I-\epsilon \left({\frac {V^{3}}{ 3}}-V\right),

L{\frac {dI}{dt}}=-V

där koefficienten ε antas vara liten. Dessa ekvationer kan kombineras till en andra ordningens differentialekvation

C{\frac {d^{2}V}{dt^{2}}}+\ epsilon \left(V^{2}-1\right){\frac {dV}{dt}}+{\frac {V}{L}}=0.

Denna van der Pol -ekvation har stimulerat mycket forskning inom matematiken för icke-linjära dynamiska system . Op-amp- kretsar som realiserar FHN- och van der Pol-modellerna av aktionspotentialen har utvecklats av Keener.

- Nagumo utvecklades av Morris och Lecar 1981 och applicerades på havstulpanens muskelfiber . Trogen havstulpanens fysiologi ersätter Morris-Lecar-modellen den spänningsstyrda natriumströmmen i Hodgkin-Huxley-modellen med en spänningsberoende kalciumström. Det finns ingen inaktivering (ingen h -variabel) och kalciumströmmen utjämnas omedelbart, så att det återigen bara finns två tidsberoende variabler: transmembranspänningen V och kaliumportsannolikheten n . Sprickbildning, indragning och andra matematiska egenskaper hos denna modell har studerats i detalj.

De enklaste modellerna av aktionspotentialen är "spolning och fyll"-modeller (även kallade "integrera-och-avfyra"-modeller), där insignalen summeras ("fyllningsfasen") tills den når en tröskel, avfyrar en puls och återställ summeringen till noll ("spolningsfasen"). Alla dessa modeller kan uppvisa entrainment , vilket vanligtvis observeras i nervsystemet.

Extracellulära potentialer och strömmar

Medan ovanstående modeller simulerar transmembranspänningen och strömmen vid en enda membranfläck, hänför sig andra matematiska modeller till spänningarna och strömmarna i den joniska lösningen som omger neuronen. Sådana modeller är användbara för att tolka data från extracellulära elektroder, som var vanliga före uppfinningen av glaspipettelektroden som möjliggjorde intracellulär inspelning. Det extracellulära mediet kan modelleras som en normal isotrop jonlösning ; i sådana lösningar följer strömmen de elektriska fältlinjerna , enligt kontinuumformen av Ohms lag

\mathbf {j} =\sigma \mathbf {E}

där j och E är vektorer som representerar strömtätheten respektive det elektriska fältet , och där σ är konduktiviteten . Således j hittas från E , som i sin tur kan hittas med Maxwells ekvationer . Maxwells ekvationer kan reduceras till ett relativt enkelt problem med elektrostatik , eftersom jonkoncentrationerna ändras för långsamt (jämfört med ljusets hastighet ) för att magnetiska effekter ska vara viktiga. Den elektriska potentialen φ( x ) vid valfri extracellulär punkt x kan lösas med hjälp av Greens identiteter

\phi (\mathbf { x} )={\frac {1}{4\pi \sigma _{\mathrm {utanför} }}}\oint _{\mathrm {membran} }{\frac {\partial }{\partial n}}{ \frac {1}{\left|\mathbf {x} -{\boldsymbol {\xi }}\right|}}\left[\sigma _{\mathrm {outside} }\phi _{\mathrm {outside} }({\boldsymbol {\xi }})-\sigma _{\mathrm {inside} }\phi _{\mathrm {inside} }({\boldsymbol {\xi }})\right]dS

där integrationen är över hela membranets yta; ${\boldsymbol {\xi }}$ är en position på membranet, σ _inuti och φ _inuti är konduktiviteten och potentialen precis inom membranet, och σ _utanför och φ _utanför motsvarande värden strax utanför membranet. Sålunda, givet dessa σ- och φ-värden på membranet, kan den extracellulära potentialen φ( x ) beräknas för vilken position x som helst ; i sin tur kan det elektriska fältet E och strömtätheten j beräknas från detta potentialfält.

Se även

Vidare läsning

Glass L, Mackey MC (1988). Från klockor till kaos: livets rytmer . Princeton, New Jersey: Princeton University. ISBN 978-0-691-08496-1 .