Central binomial koefficient

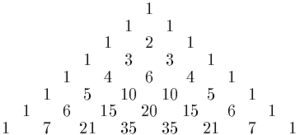
Pascals triangel, raderna 0 till 7. Siffrorna i den centrala kolumnen är de centrala binomialkoefficienterna.

I matematik är den n : te centrala binomialkoefficienten den speciella binomialkoefficienten

${2n \choose n}={\frac {(2n)!}{(n!)^{2}} }=\prod \limits _{k=1}^{n}{\frac {n+k}{k}}{\text{ för alla }}n\geq 0.$

De kallas centrala eftersom de dyker upp exakt i mitten av de jämna raderna i Pascals triangel . De första centrala binomialkoefficienterna som börjar på n = 0 är:

1 , 2 , 6 , 20 , 70 , 252 , 924, 3432, 12870, 48620, ...; (sekvens A000984 i OEIS )

Egenskaper

De centrala binomialkoefficienterna representerar antalet kombinationer av en mängd där det finns lika många två typer av objekt.

Till exempel representerar $n=2$ AABB, ABAB, ABBA, BAAB, BABA, BBAA .

De representerar också antalet kombinationer av A och B där det aldrig finns fler B än A.

Till exempel representerar $n=2$ AAAA, AAAB, AABA, AABB, ABAA, ABAB .

Antalet faktorer av 2 i ${\binom {2n}{n}}$ är lika med antalet ettor i den binära representationen av n , så 1 är den enda udda centrala binomialkoefficienten.

Genererande funktion

Den ordinarie genererande funktionen för de centrala binomialkoefficienterna är

$${\frac {1}{\sqrt {1-4x}}}=\sum _{n=0}^{\infty }{\binom {2n}{n}}x^{n}=1 +2x+6x^{2}+20x^{3}+70x^{4}+252x^{5}+\cdots .$$

Detta kan bevisas med hjälp av binomialserien och relationen

$${\binom {2n}{n}}=(-1)^{n}4^{n}{\ binom {-1/2}{n}},$$

där $}}}$ n en generaliserad binomial koefficient

De centrala binomialkoefficienterna har exponentiell genererande funktion

$$\sum _{n=0}^{\infty }{\binom {2n}{n}}{\frac {x^{n}}{n!} }=e^{2x}I_{0}(2x),$$

₀ där I är en modifierad Bessel-funktion av det första slaget .

Den genererande funktionen för kvadraterna av de centrala binomialkoefficienterna kan skrivas i termer av den fullständiga elliptiska integralen av det första slaget :

$\sum _{n=0}^{\infty }{\binom {2n}{n}}^{2}x^{n}={\frac {4}{\pi (1+{\ sqrt {1-16x}})}}K\vänster({\frac {1-{\sqrt {1-16x}}}{1+{\sqrt {1-16x}}}}\höger).$

Asymptotisk tillväxt

Wallis -produkten kan skrivas med begränsningar:

${\frac {\pi }{2}}=\lim _{n\to \infty }\prod _{k=1}^{n}{\frac {2k\ cdot 2k}{(2k-1)(2k+1)}}=\lim _{n\to \infty }{\frac {4^{n}n!^{2}}{(2n-1)! !(2n+1)!!}}=\lim _{n\to \infty }4^{n}n!^{2}{\frac {2^{2n}n!^{2}}{( 2n)!^{2}(2n+1)}}$

eftersom $(2n)!=2^{n}n!(2n-1)!!$ .

Att ta kvadratroten från båda sidor ger asymptoten för den centrala binomialkoefficienten:

${2n \choose n}\sim {\frac {4^{n}}{\sqrt {\pi n}}}$ .

Det senare kan också fastställas med hjälp av Stirlings formel . Å andra sidan kan den också användas som ett sätt att bestämma konstanten ${\sqrt {2\pi }}$ framför Stirlingformeln.

Uppskattningar

Enkla gränser som omedelbart följer av $4^{n}=(1+1)^{2n}=\summa _{ k=0}^{2n}{\binom {2n}{k}}$ är

${\frac {4^{n}}{2n+1}}\leq {2n \choose n}\leq 4^ {n}{\text{ för alla }}n\geq 0$

Några bättre gränser är

${\frac {4^{n}}{\sqrt {\pi (n+{\frac { 1}{2}})}}}\leq {2n \choose n}\leq {\frac {4^{n}}{\sqrt {\pi n}}}{\text{ för alla }}n\ geq 1$

Relaterade sekvenser

De närbesläktade katalanska talen C _n ges av:

$C_{n}={\frac {1}{n+1 }}{2n \choose n}={2n \choose n}-{2n \choose n+1}{\text{ för alla }}n\geq 0.$

En lätt generalisering av centrala binomialkoefficienter är att ta dem som ${\displaystyle {\frac {\Gamma (2n+1$ n , där $\Gamma (x)$ är gammafunktionen och $\mathrm {B} (x,y)$ är betafunktionen .

Krafterna av två som delar de centrala binomialkoefficienterna ges av Goulds sekvens , vars n :te element är antalet udda heltal i rad n i Pascals triangel.

Kvadrering genereringsfunktionen ger

${\frac {1}{1-4x}}=\summa _{n= 0}^{\infty }{\binom {2n}{n}}x^{n}\summa _{n=0}^{\infty }{\binom {2n}{n}}x^{n}$

Att jämföra koefficienterna för $x^{n}$ ger

$\sum _{k=0}^{n}{\binom {2k}{k}}{\binom {2n-2k}{nk}}=4^{n}$

Till exempel, $64=1(20)+2(6)+6(2)+20(1)$ . (sekvens A000302 i OEIS )

Annan information

Halva centrala binomialkoefficienten $\textstyle {\frac {1}{2}}{2n \choose n}={2n-1 \choose n-1}$ (för $n>0$ ) (sekvens A001700 i OEIS ) ses i Wolstenholmes sats .

Enligt Erdős kvadratfria gissningar , bevisade 1996, är ingen central binomial koefficient med n > 4 kvadratfri .

$\textstyle {\binom {2n}{n}}$ är summan av kvadraterna på den n -te raden i Pascals triangel:

${2n \choose n}=\summa _{k=0}^{n}{\binom {n}{k}}^{2 }$

Till exempel, ${\tbinom {6}{3}}=20=1^{2}+3^{2}+3 ^{2}+1^{2}$ .

Erdős använder i stor utsträckning centrala binomialkoefficienter i sitt bevis på Bertrands postulat .

Ett annat anmärkningsvärt faktum är att styrkan av 2 som delar $(n+1)\dots (2n)$ är exakt n .

Se även

• Central trinomial koefficient

•   Koshy, Thomas (2008), Catalan Numbers with Applications , Oxford University Press, ISBN 978-0-19533-454-8 .

externa länkar

• Central binomial koefficient på PlanetMath .