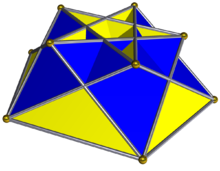
Korsad femkantig kuploid

Korsad femkantig kuploid
Ansikten	5 trianglar 5 rutor 1 femkant
Kanter	20
Vertices	10
Vertex-konfiguration	5(5.4. 3 / 2 .4) 5(3.4. 3 / 2 . 4 / 3 )
Symmetrigrupp	C 5v , [5], (*55)
Rotationsgrupp	C 5 , [5] + , (55)
Dubbel polyeder	korsad pentagonal keratinoid
Egenskaper	icke-orienterbar

3D-modell av en korsad femkantig kuploid

Inom geometrin är den korsade femkantiga kupolen eller den korsade femkantiga halvkupolen en medlem av den oändliga familjen av kuploider . Det kan erhållas som en skiva av den stora komplexa rhombicosidodecahedron. Som i alla kupoler har baspolygonen dubbelt så många kanter och hörn som toppen ; men i } det här fallet . 5/4 10/4 är baspolygonen ett degenererat { dekagram , eftersom toppen är en { } femhörning Därför dras den degenererade basen tillbaka och trianglarna kopplas till kvadraterna istället.

Det kan ses som en kupol med en retrograd femkantig bas, så att kvadraterna och trianglarna ansluter över baserna på motsatt sätt till den femkantiga kupolen , och korsar därmed varandra.

Besläktade polyedrar

Familj av stjärnkuploider

n ⁄ d	3	5	7
2	Korsad triangulär kuploid	Pentagrammisk kuploid	Heptagrammisk kuploid
4	—	Korsad femkantig kuploid	Korsad heptagrammisk kuploid

Den korsade femkantiga kuploiden kan ses som en sektion av den degenererade enhetliga polyedern känd som den stora komplexa rhombicosidodecahedron:

Korsad femkantig kuploid	Stor komplex rhombicosidodecahedron
Liten ditrigonal icosidodecahedron	Ditrigonal dodecadodecahedron	Stor ditrigonal icosidodecahedron	Sammansättning av fem kuber

(På bilden av den korsade femkantiga kuploiden är femhörningen röd (längst ner och inte synlig), rutorna gula och trianglarna blå. På bilden av den lilla komplexa rhombicosidodecahedron är femhörningarna röda, rutorna blå ( gömd inuti och inte synlig), och trianglarna gula.)

Att ta en femhörning från den stora komplexa rhombicosidodecahedron, sedan ta de fem kvadraterna som gränsar till den, och sedan ta de fem trianglarna som gränsar till dessa rutor resulterar i en korsad femkantig kuploid. kantfasadering Eftersom denna korsade femkantiga kuploid sålunda delar alla sina kanter med denna polyeder, kan den kallas en av den. De icke degenererade likformiga polyedrarna som delar samma kanter som den lilla komplexa rhombicosidodecahedron är de tre ditrigonala polyedrarna , såväl som den regelbundna sammansättningen av fem kuber : därför är den korsade femkantiga kuploiden också en kantfasadering av dessa polyedrar.

Som 5 / 4 < 2, har den korsade femkantiga kuploiden inte ett membran som den pentagrammiska kuploiden har.

Dubbel polyeder

3D-modell av en korsad femkantig keratinoid

Den dubbla av den korsade femkantiga kuploiden har 5 drake- och 5 antiparallelogramytor , och kan kallas den korsade femkantiga keratinoiden efter Inchbald, eftersom den är formad som ett ihåligt horn:

• Guy Inchbald, Fylla polytoper
• Richard Klitzing, Axial-Symmetrical Edge Facets of Uniform Polyhedra
• Jim McNeill, The 5/2 semicupola and 5/4 semicupola
• Jim McNeill, Semikupoler
• Ulrich Mikloweit, Fasetteringar av enhetliga polyedrar

externa länkar

• Pappersmodell av denna polyeder av Robert Webb