Kaufmann–Bucherer–Neumann experiment

Figur 1. Walter Kaufmanns mätning av elektronladdning-till-massaförhållandet för elektronens olika hastigheter. En radiumkälla i botten av den evakuerade apparaten avgav beta-partiklar med varierande energi. Parallella E- och B -fält i kombination med nålhålsöppningen tillät endast vissa kombinationer av elektronriktning och hastighet att exponera den fotografiska plattan i toppen. (a) Denna frontvy av apparaten illustrerar den enhetliga accelerationen som de laddade kondensatorplattorna utsätter beta-partiklarna. (b) Denna sidovy av apparaten illustrerar den cirkulära rörelsen av beta-partiklarna tvärs B -fältet. (c) Den fotografiska plattan registrerade en krökt strimma som analyserades för att bestämma e/m för varierande v efter olika teoretiska antaganden.

Kaufmann –Bucherer–Neumann-experimenten mätte beroendet av ett objekts tröghetsmassa (eller rörelsemängd ) på dess hastighet . Den historiska betydelsen av denna serie experiment utförda av olika fysiker mellan 1901 och 1915 beror på resultaten som används för att testa förutsägelserna om speciell relativitet . Den utvecklande precisionen och dataanalysen av dessa experiment och det resulterande inflytandet på teoretisk fysik under dessa år är fortfarande ett ämne för aktiv historisk diskussion, eftersom de tidiga experimentella resultaten först stred mot Einsteins då nyligen publicerade teori (1905), men senare versioner av detta experiment bekräftade det. För moderna experiment av det slaget, se Tester av relativistisk energi och momentum , för allmän information se Tester av speciell relativitet .

Historiska sammanhang

1896 upptäckte Henri Becquerel radioaktivt sönderfall i en mängd olika kemiska element . Därefter beta-strålningen från dessa sönderfall vara emission av en negativt laddad partikel . Senare identifierades dessa partiklar med elektronen , upptäckt i katodstråleexperiment av JJ Thomson 1897.

Detta var kopplat till den teoretiska förutsägelsen av den elektromagnetiska massan av JJ Thomson 1881, som visade att den elektromagnetiska energin bidrar till massan av en laddad kropp i rörelse . Thomson (1893) och George Frederick Charles Searle (1897) beräknade också att denna massa beror på hastighet och att den blir oändligt stor när kroppen rör sig med ljusets hastighet i förhållande till den lysande etern . Även Hendrik Antoon Lorentz (1899, 1900) antog ett sådant hastighetsberoende som en konsekvens av hans teori om elektroner. Vid denna tidpunkt separerades den elektromagnetiska massan i "tvärgående" och "längsgående" massa, och betecknades ibland som "skenbar massa", medan den invarianta Newtonska massan betecknades som "verklig massa". Å andra sidan var det den tyske teoretikern Max Abrahams övertygelse att all massa i slutändan skulle visa sig vara av elektromagnetiskt ursprung, och att den newtonska mekaniken skulle inordnas i elektrodynamikens lagar.

1904 föreslog Lorentz att massan längs rörelsebanan (längsmassan) och massan i riktningarna vinkelräta mot rörelsen (tvärgående) är olika. I hans teori är den längsgående massan $m_{L}={{\gamma }^{3}}m$ och den tvärgående massan $m_{T}= {\gamma }m$ , där $\gamma$ är Lorentz-faktorn och $m$ är resten av elektronen. Begreppet (tvärgående) elektromagnetisk massa ${\displaystyle m_{T}} ,$ som baserades på specifika modeller av elektronen, omvandlades senare till det rent kinematiska konceptet relativistisk massa som berör alla former av energi, inte bara elektromagnetisk energi. För närvarande används emellertid begreppet relativistisk massa, även om det fortfarande ofta refereras till i populära verk om relativitetsteori, numera sällan bland professionella arbetande fysiker och har ersatts av uttrycken för relativistisk energi och momentum, som också förutspår att hastigheten på ljus kan inte nås av massiva kroppar. Detta beror på att alla dessa relationer involverar Lorentz-faktorn :

${\frac {m_{T}}{m}}={\frac {p}{mv}}={\ frac {E}{mc^{2}}}={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}$

Därför kan Bucherer–Kaufmann–Neumann-experimenten ses som tidiga tester av relativistisk energi och momentum . (För följande historiska beskrivning av experimenten används fortfarande begreppen "tvärgående" eller "relativistisk massa").

Kaufmanns experiment

Första experimenten

Figur 2. Kaufmanns mätningar från 1901 (korrigerade 1902) visade att förhållandet mellan laddning och massa minskar och därmed ökar elektronens rörelsemängd (eller massa) med hastigheten. Observera att $\scriptstyle \epsilon /m_{0}\sim 1,95\ gånger 10^{7}$ emu/gm när elektronen är i vila.

Walter Kaufmann började experimentera med beta-strålar med en anordning som liknar ett katodstrålerör , där källan till elektronerna var sönderfallet av radium som placerades i en evakuerad behållare. (Se fig. 1) Sådana strålar som emitterades från radium kallades på den tiden "Becquerel-strålar". I motsats till de då kända katodstrålarna som nådde hastigheter endast upp till 0,3 c, där c är ljusets hastighet, nådde Becquerel-strålar hastigheter upp till 0,9 c . Men eftersom beta-partiklar har olika hastigheter var strålningen inhomogen. Därför applicerade Kaufmann elektriska och magnetiska fält inriktade parallellt med varandra, så att avböjningarna som orsakades av dem var vinkelräta mot varandra. Deras nedslag på en fotografisk platta producerade en avböjningskurva, vars individuella punkter motsvarade en viss hastighet och en viss massa av elektronerna. Genom att vända laddningen på kondensorn, och därmed invertera det elektriska fältet, kunde två symmetriska kurvor erhållas, vars mittlinje bestämde riktningen för den magnetiska avböjningen.

Kaufmann publicerade en första analys av sina data 1901 - han kunde faktiskt mäta en minskning av förhållandet mellan laddning och massa, vilket visade att massa eller rörelsemängd ökar med hastigheten. Med hjälp av Searles formel (1897) för den elektromagnetiska energiökningen av laddade kroppar med hastighet, beräknade han ökningen av elektronens elektromagnetiska massa som en funktion av hastigheten:

$\phi (\beta )={\frac {3}{4 \beta ^{2}}}\left[{\frac {1}{\beta }}\lg {\frac {1-\beta }{1+\beta }}+{\frac {2}{1- \beta ^{2}}}\right],\;\beta ={\frac {v}{c}}$ ,

Kaufmann märkte att den observerade ökningen inte kan förklaras med denna formel, så han separerade den uppmätta totala massan i en mekanisk (sann) massa och en elektromagnetisk (skenbar) massa , den mekaniska massan är betydligt större än den elektromagnetiska. Han gjorde dock två misstag: Som visat av Max Abraham förbise Kaufmann att Searles formel bara gäller i längdriktningen, men för avböjningsmätningar var formeln för tvärriktningen viktig. Därför introducerade Abraham den "tvärgående elektromagnetiska massan" med följande hastighetsberoende:

$\phi (\beta )={\frac {3}{4\beta ^{ 2}}}\left({\frac {1+\beta ^{2}}{2\beta }}\lg {\frac {1+\beta }{1-\beta }}-1\right),$

Kaufmann gjorde också ett beräkningsfel när han härledde avböjningskurvorna. Dessa fel korrigerades av honom 1902.

1902 och 1903 utförde Kaufmann ytterligare en serie tester med uppdaterade och förbättrade experimentella tekniker. Resultaten tolkades av honom som en bekräftelse på Abrahams teori och på antagandet att elektronens massa är helt av elektromagnetiskt ursprung.

Hermann Starke genomförde liknande mätningar 1903, även om han använde katodstrålar begränsade till 0,3c. Resultaten som han erhöll tolkades av honom som att de överensstämde med Kaufmanns.

Tävlande teorier

Figur 3. Förutsägelser av hastighetsberoende för tvärgående elektromagnetisk massa enligt Abrahams, Lorentz och Bucherers teorier.

1902 publicerade Max Abraham en teori baserad på antagandet att elektronen var en stel, perfekt sfär , med dess laddning jämnt fördelad på dess yta. Som förklarats ovan introducerade han den så kallade "tvärgående elektromagnetiska massan" förutom den "längsgående elektromagnetiska massan", och hävdade att hela elektronmassan är av elektromagnetiskt ursprung.

Samtidigt utvidgade Lorentz (1899, 1904) sin teori om elektroner och antog att en elektrons laddning spreds över hela dess volym och att i Kaufmanns experiment skulle dess form komprimeras i rörelseriktningen och förbli oförändrad i tvärriktningarna. Till Kaufmanns förvåning kunde Lorentz visa att hans modell också stämde överens med hans experimentella data. Denna modell utvecklades ytterligare och fulländades av Henri Poincaré (1905), så att Lorentz teori nu överensstämde med relativitetsprincipen .

En liknande teori utvecklades av Alfred Bucherer och Paul Langevin 1904, med skillnaden att den totala volymen som upptas av den deformerade elektronen antogs oförändrad. Det visade sig att denna teoris förutsägelse låg närmare Abrahams teori än Lorentz.

Slutligen förutspådde Albert Einsteins speciella relativitetsteori ( 1905) förändringen av den punktliknande elektronens massa på grund av egenskaperna hos transformationen mellan partikelns viloram och laboratorieramen där mätningarna utfördes. Matematiskt förutsäger denna beräkning samma beroende mellan hastighet och massa som Lorentz teori, även om den antar mycket olika fysiska begrepp.

När det gäller ökningen av tvärgående elektromagnetisk massa var förutsägelserna från de olika teorierna (Fig. 3):

${\begin{aligned}&{\text{Abraham}}&\phi (\beta )&={\frac {3}{4 \beta ^{2}}}\left({\frac {1+\beta ^{2}}{2\beta }}\lg {\frac {1+\beta }{1-\beta }}-1 \right)\\&{\text{Lorentz--Einstein}}&\phi (\beta )&=(1-\beta ^{2})^{-1/2}\\&{\text{Bucherer --Langevin}}&\phi (\beta )&=(1-\beta ^{2})^{-1/3}\end{aligned}}$

Experiment 1905

För att fatta ett beslut mellan dessa teorier utförde Kaufmann återigen sina experiment med högre precision. Kaufmann trodde att han definitivt hade motbevisat Lorentz-Einsteins formel och hade därför också motbevisat relativitetsprincipen . Enligt hans uppfattning låg de enda återstående alternativen mellan Abrahams och Bucherers teorier. Lorentz var förbryllad och skrev att han var " i slutet av sitt latinska ".

Men kritik mot Kaufmanns experiment uppstod. Kort efter att Kaufmann publicerat sina resultat och slutsatserna av sin analys, Max Planck för att omanalysera de data som erhölls genom experimentet. 1906 och 1907 publicerade Planck sin egen slutsats om beteendet hos elektronernas tröghetsmassa med höga hastigheter. Med bara nio datapunkter från Kaufmanns publikation 1905 räknade han om den exakta uppställningen av fälten för varje punkt och jämförde mätningarna mot förutsägelserna från de två konkurrerande teorierna. Han visade att Kaufmanns resultat inte är helt avgörande och skulle leda till superluminala hastigheter. Einstein anmärkte 1907 att även om Kaufmanns resultat stämde bättre överens med Abrahams och Bucherers teorier än med hans egna, så var grunderna för de andra teorierna inte rimliga och hade därför endast liten sannolikhet att vara korrekta.

Efterföljande experiment

Bucherer

Figur 4. Ovanifrån. Bucherers experimentupplägg.

Figur 5. Tvärsnitt genom den cirkulära kondensatorns axel vid vinkeln α med avseende på magnetfältet H.

Huvudproblemet med Kaufmanns experiment var hans användning av parallella magnetiska och elektriska fält, vilket påpekades av Adolf Bestelmeyer (1907). Genom att använda en metod baserad på vinkelräta magnetiska och elektriska fält (introducerad av JJ Thomson och vidareutvecklad till ett hastighetsfilter av Wilhelm Wien ) erhöll Bestelmeyer avsevärt olika värden för förhållandet laddning till massa för katodstrålar upp till 0,3c. Bestelmeyer tillade dock att hans experiment inte var tillräckligt exakt för att ge ett definitivt beslut mellan teorierna.

Därför utförde Alfred Bucherer (1908) en exakt mätning med hjälp av ett hastighetsfilter liknande Bestelmeyers. Se figurerna. 4 & 5. En radium betakälla placerades i mitten av en cirkulär kondensor bestående av två försilvrade glasplattor åtskilda 0,25 mm från varandra och laddade till cirka 500 volt, inställda i ett homogent 140 Gauss magnetfält. Radium emitterade beta-strålar i alla riktningar, men i någon speciell riktning α, lämnade endast de beta-strålar hastighetsfiltret vars hastighet var sådan att de elektriska och magnetiska fälten exakt kompenserade varandra. Efter att ha lämnat kondensorn, avböjdes strålarna av magnetfältet och exponerade en fotografisk platta som var parallell med kondensorns kant och vinkelrätt mot de icke-avböjda strålarna.

Figur 6. Bucherers data i fem körningar.

Figur 7. Wolz data i 13 körningar.

För sin slutliga analys räknade Bucherer om de uppmätta värdena för fem körningar med Lorentz respektive Abrahams formler, för att erhålla förhållandet laddning till massa som om elektronerna var i vila. Eftersom förhållandet inte varierar för vilande elektroner bör datapunkterna ligga på en enda horisontell linje (se fig. 6). Detta var dock ungefär bara i fallet då uppgifterna beräknades med Lorentz formel, medan resultaten av Abrahams formel avvek kraftigt (de röda och blå linjerna representerar medelvärdet enligt båda formlerna). Överensstämmelsen med Lorentz-Einstein-formeln tolkades av Bucherer som en bekräftelse av relativitetsprincipen och Lorentz-Einstein-teorin - ett resultat som omedelbart applåderades av Lorentz, Einstein och Hermann Minkowski .

Dessutom förbättrades Bucherers apparat 1909 av hans elev Kurt Wolz, som också fick överensstämmelse med Lorentz-Einstein-formeln (även om han inte jämförde Abrahams formel med hans data, Fig. 7).

Även om många fysiker accepterade Bucherers resultat, fanns det fortfarande vissa tvivel. Till exempel publicerade Bestelmeyer en artikel där han tvivlade på giltigheten av Bucherers resultat. Han hävdade att ett experiment ensamt inte kan fastställa riktigheten av en viktig fysisk lag, att Bucherers resultat kan bli avsevärt förvrängt av icke-kompenserade strålar som når den fotografiska plattan, och att omfattande dataprotokoll och felanalys är nödvändiga. En polemisk tvist mellan dessa två forskare följde i en serie publikationer, där Bestelmeyer hävdade att Wolz experiment påverkas av samma problem.

Hupka

Till skillnad från Kaufmann och Bucherer använde Karl Erich Hupka (1909) katodstrålar vid 0,5c för sina mätningar. Strålningen (genererad vid en kopparkatod) accelererades kraftigt av fältet mellan katod och anod i ett högt evakuerat urladdningsrör. Anoden som tjänade som ett diafragma passerades av strålen med konstant hastighet och ritade skuggbilden av två Wollaston-trådar på en fosforescerande skärm bakom ett andra diafragma. Om en ström genererades bakom detta diafragma, avböjdes strålen och skuggbilden förflyttades. Resultaten överensstämde med Lorentz-Einstein, även om Hupka påpekade att detta experiment inte representerade ett definitivt resultat. Därefter publicerade W. Heil några artiklar som handlade om kritik och tolkningar av resultatet, som Hupka svarade på.

Neumann och Guye/Lavanchy

Figur 8. Neumanns utvärdering av 26 datapunkter för varje teori.

År 1914 genomförde Günther Neumann nya mätningar med Bucherers utrustning, och gjorde i synnerhet vissa förbättringar för att ta itu med Bestelmeyers kritik, särskilt frågan om icke-kompenserade strålar, och gjorde omfattande förbättringar av dataprotokollen. Beräkningsmetoden var densamma som Bucherers (se fig. 6). Också i detta experiment ligger data som motsvarar Lorentz formel nästan på en horisontell linje efter behov, medan data som erhålls från Abrahams formel avviker kraftigt (se fig. 8). Neumann drog slutsatsen att hans experiment stämde överens med Bucherers och Hupkas, vilket definitivt bevisade Lorentz-Einstein-formeln i intervallet 0,4–0,7c, och motbevisade Abrahams formel. Instrumentella osäkerheter förekom i intervallet 0,7–0,8c, så avvikelsen från Lorentz-Einstein-formeln i detta intervall ansågs inte vara signifikant.

Figur 9. Guye och Lavanchys utvärdering av 25 datapunkter för varje teori.

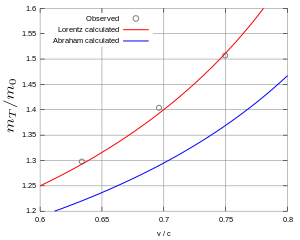
1915 mätte Charles-Eugène Guye och Charles Lavanchy avböjningen av katodstrålar vid 0,25c–0,5c. De använde ett rör med katod och anod för att påskynda strålarna. Ett diafragma vid anoden producerade en stråle som avböjdes. En skärm placerades i slutet av apparaten, vid vilken stötarna fotograferades av en kamera. De beräknade därefter förhållandet mellan den transversella elektromagnetiska massan m _T och vilomassan m ₀ indikerad av den röda och blå kurvan, och uppnådde god överensstämmelse med Lorentz-Einstein-formeln (se fig. 9), vilket kompletterade Neumanns resultat.

Neumanns och Guye/Lavanchys experiment ansågs av många som ett avgörande bevis på Lorentz-Einsteins formel. Lorentz sammanfattade dessa ansträngningar 1915:

Senare experiment [..] har bekräftat formeln [..] för den tvärgående elektromagnetiska massan, så att den enda invändning som kunde framföras mot hypotesen om den deformerbara elektronen och relativitetsprincipen med största sannolikhet nu har tagits bort .

Ytterligare utveckling

Figur 10. Rogers et al. elektrostatisk spektrograf

Zahn & Spees (1938) och Faragó & Lajos Jánossy (1954) hävdade att många antaganden som användes i dessa tidiga experiment om elektronernas natur och egenskaper och experimentuppställningen var felaktiga eller oprecisa. Precis som med Kaufmanns experiment, skulle Bucherer-Neumann-experimenten bara visa en kvalitativ massaökning och var oförmögna att avgöra mellan de konkurrerande teorierna.

Medan resultaten av dessa elektronavböjningsexperiment var omtvistade under lång tid, hade Karl Glitschers undersökningar av vätelinjernas fina struktur (baserad på Arnold Sommerfelds arbete ) redan 1917 gett en tydlig bekräftelse på Lorentz–Einstein. formel, eftersom de relativistiska uttrycken för momentum och energi var nödvändiga för att härleda den fina strukturen, och utgjorde ett vederläggande av Abrahams teori.

Figur 11. Tre datapunkter av Rogers et al. , i överensstämmelse med Lorentz-Einstein-formeln.

Dessutom utfördes de första elektronavböjningsexperimenten med tillräcklig precision av Rogers et al. (1940), som utvecklade en förbättrad uppställning. Radiumsönderfallsserien ger ett spektrum av beta-partiklar med ett brett spektrum av energier . De tidigare mätningarna av Kaufmann, Bucherer och andra hade använt platta parallella plattkondensatorer som inte gav någon fokusering av beta-partiklarna. Rogers et al. (Fig. 10) konstruerade istället en elektrostatisk spektrograf som kan lösa upp energimaxima för individuella beta-partikellinjer från radiumsönderfallsserien. Den elektrostatiska spektrografen var konstruerad av segment av två cylindrar och var innesluten i en evakuerad järnlåda. Beta-strålarna emitterades från en fin platinatråd belagd med aktiv radiumavlagring. De spridda strålarna inträffade på en slits framför en geigerräknare . Data från detta experiment kombinerades med tidigare magnetiska spektrometermätningar av H _ρ för att ge förhållandet laddning till massa, som därefter jämfördes med förutsägelserna från Lorentz och Abraham för förhållandet mellan tvärmassa och vilomassa. Punkterna var alla på kurvan som representerade Lorentz-Einstein-formeln inom 1 % (se fig. 11). Detta experiment anses vara tillräckligt exakt för att skilja mellan teorierna.

Moderna tester

Huvudartikel: Tester av relativistisk energi och momentum

Sedan dess har många ytterligare experiment beträffande det relativistiska energi-momentum-förhållandet utförts, inklusive mätningar av elektroners avböjning, alla bekräftar speciell relativitet med hög precision. Även i moderna partikelacceleratorer bekräftas förutsägelserna om speciell relativitet rutinmässigt.

Se även

• Special relativitetsteoriens historia

Sekundära källor

• Battimelli, G. (1981). "Electronens elektromagnetiska massa: en fallstudie av ett icke-avgörande experiment". Fundamenta Scientiae . 2 : 137–150.
• Janssen, Michel; Mecklenburg, Matthew (2007), "Från klassisk till relativistisk mekanik: Elektromagnetiska modeller av elektronen", i VF Hendricks; et al. (red.), Interaktioner: Mathematics, Physics and Philosophy , Dordrecht: Springer, s. 65–134

• Lorentz, Hendrik Antoon (1916), Theory of elektrons and its applications to the lights and radiant heat at the Internet Archive , Leipzig & Berlin: BG Teubner {{ citation }} : Extern länk i |title= ( hjälp )

•   Miller , Arthur I. (1981), Albert Einsteins speciella relativitetsteori. Emergence (1905) och tidig tolkning (1905–1911), Läsning: Addison–Wesley, ISBN 0-201-04679-2

•   Pais, Abraham (2005) [Först publicerad 1982], Subtle is the Lord: The Science and the Life of Albert Einstein , New York: Oxford University Press, ISBN 0-19-280672-6

• Pauli, Wolfgang (1921), "Die Relativitätstheorie" , Encyclopädie der Mathematischen Wissenschaften , 5 (2): 539–776

På engelska:   Pauli, W. (1981) [1921]. Relativitetsteori . Fysikens grundläggande teorier . Vol. 165. Dover Publikationer. ISBN 0-486-64152-X .

•   Staley, Richard (2008), Einsteins generation , Chicago: University Press, ISBN 978-0-226-77057-4

externa länkar

• Presentation om Kaufmann-experiment (PowerPoint)
• Lista över SR-tester