Kaotisk spridning

Kaotisk spridning är en gren av kaosteorin som handlar om spridningssystem som uppvisar en stark känslighet för initiala förhållanden . I ett klassiskt spridningssystem kommer det att finnas en eller flera slagparametrar, b , där en partikel skickas in i spridaren. Detta ger upphov till en eller flera utgångsparametrar, y , när partikeln går ut mot oändligheten. Medan partikeln passerar systemet kan det också finnas en fördröjningstid , T - den tid det tar för partikeln att lämna systemet - förutom den tillryggalagda sträckan s , som i vissa system, dvs "biljardliknande" " system där partikeln genomgår förlustfria kollisioner med hårda , fasta föremål, kommer de två att vara likvärdiga - se nedan. I ett kaotiskt spridningssystem kan en mycket liten förändring av påverkansparametern ge upphov till en mycket stor förändring av utgångsparametrarna.

Gaspard-Rice system

Fig. 1: Diagram över Gaspard-Rice-spridningssystem som visar huvudparametrar.

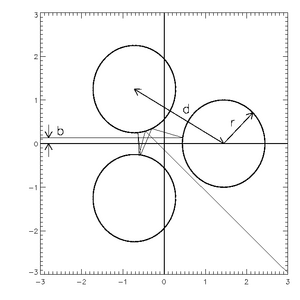
Ett utmärkt exempelsystem är spridningssystemet "Gaspard–Rice" (GR) - även känt som "tre-skivor"-systemet - som förkroppsligar många av de viktiga begreppen i kaotisk spridning samtidigt som det är enkelt och lätt att förstå och simulera. Konceptet är väldigt enkelt: vi har tre hårdskivor arrangerade i någon triangulär formation, en punktpartikel skickas in och genomgår perfekta, elastiska kollisioner tills den går ut mot oändligheten. I denna diskussion kommer vi bara att överväga GR-system som har lika stora skivor, lika fördelade runt punkterna i en liksidig triangel.

Figur 1 illustrerar detta system medan figur 2 visar två exempel på banor. Observera först att banorna studsar runt systemet under en tid innan de slutligen går ur. Observera också att om vi anser att påverkansparametrarna är början på de två perfekt horisontella linjerna till vänster (systemet är helt reversibelt: utgångspunkten kan också vara ingångspunkten), är de två banorna initialt så nära att de är nästan identisk. När de går ut är de helt olika, vilket illustrerar den starka känsligheten för initiala förhållanden. Detta system kommer att användas som ett exempel i hela artikeln.

Fig. 2: Gaspard-risspridningssystem som visar känslighet för initiala förhållanden.

Nedbrytningshastighet

Om vi introducerar ett stort antal partiklar med jämnt fördelade slagparametrar, kallas hastigheten med vilken de lämnar systemet sönderfallshastigheten. Vi kan beräkna avklingningshastigheten genom att simulera systemet under många försök och bilda ett histogram över fördröjningstiden, T . För GR-systemet är det lätt att se att fördröjningstiden och längden på partikelbanan är ekvivalenta men för en multiplikationskoefficient. Ett typiskt val för islagsparametern är y -koordinaten, medan banavinkeln hålls konstant vid noll grader – horisontell. Samtidigt säger vi att partikeln har "gått ur systemet" när den väl passerar en gräns på ett godtyckligt, men tillräckligt stort, avstånd från systemets mitt.

Vi förväntar oss att antalet partiklar som finns kvar i systemet, N(T) , kommer att variera som:

N(T)\sim e^{-\gamma T}

Sålunda ges avklingningshastigheten , $\gamma$ , som:

\gamma =\lim _{n\rightarrow \infty }-{\frac {\ln N(T)}{T}}

där n är det totala antalet partiklar.

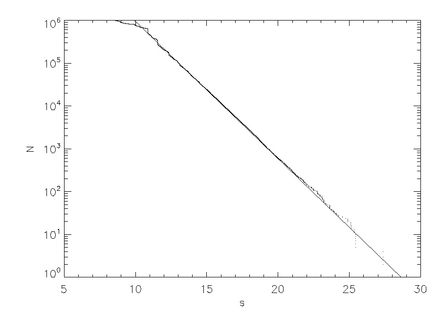
Figur 3 visar en kurva över väglängden mot antalet partiklar för en simulering av en miljon (1e6) partiklar som startas med slumpmässig anslagsparameter, b . En anpassad rak linje med negativ lutning, $\gamma =0,739$ överlagras. Banlängden, s , är ekvivalent med avklingningstiden, T , förutsatt att vi skalar (konstant) hastigheten på lämpligt sätt. Observera att en exponentiell avklingningshastighet är en egenskap specifikt för hyperbolisk kaotisk spridning. Icke-hyperboliska spridare kan ha en aritmetisk avklingningshastighet.

Fig. 3: Nedbrytningshastighet för spridningssystemet Gaspard-Rice.

Ett experimentellt system och det stabila grenröret

Fig. 4: Ett experimentellt Gaspard-Rice-spridningssystem.

Figur 4 visar en experimentell realisering av Gaspard-Rice-systemet med hjälp av en laser istället för en punktpartikel. Som alla som faktiskt har provat detta vet är detta inte en särskilt effektiv metod för att testa systemet – laserstrålen sprids åt alla håll. Som framgår av Sweet, Ott och Yorke är en mer effektiv metod att rikta färgat ljus genom mellanrummen mellan skivorna (eller i det här fallet, tejpa färgade pappersremsor över par av cylindrar) och se reflektionerna genom ett öppet gap. Resultatet är ett komplext mönster av ränder med växlande färg, som visas nedan, tydligare i den simulerade versionen nedan.

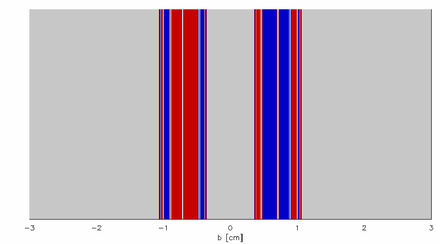
Figurerna 5 och 6 visar attraktionsbassängerna för varje anslagsparameter, b , det vill säga för ett givet värde på b , genom vilket gap kommer partikeln ut? Bassängens gränser bildar en Cantor-uppsättning och representerar medlemmar av det stabila grenröret : banor som, när de väl startat, aldrig lämnar systemet.

Fig. 5: Ett experimentellt Gaspard-Rice-spridningssystem som visar attraktionsbassänger.

Fig 6: Simulering av spridningssystemet Gaspard-Rice som visar attraktionsbassänger.

Den invarianta mängden och den symboliska dynamiken

Fig. 7: Möjliga variabler för att representera Gaspard-Rice-systemet som en itererad funktionskarta.

Så länge det är symmetriskt kan vi lätt tänka på systemet som en itererad funktionskarta , en vanlig metod för att representera ett kaotiskt, dynamiskt system. Figur 7 visar en möjlig representation av variablerna, där den första variabeln, $\theta \in [-\pi ,\pi ]$ , representerar vinkeln runt skivan vid rebound och andra, $\phi \in [-\pi /2,\pi /2]$ , som representerar anslags-/reboundvinkeln relativt skivan. En delmängd av dessa två variabler, kallad den invarianta uppsättningen, kommer att mappa till sig själva. Denna uppsättning, vars fyra delar visas i figurerna 8 och 9, kommer att vara fraktal , totalt icke-attraherande och mäta noll. Detta är en intressant inversion av de mer normalt diskuterade kaotiska systemen där den fraktala invarianta uppsättningen attraherar och i själva verket består av attraktionsbassängen. Observera att den invarianta mängdens totalt icke-attraherande karaktär är en annan egenskap hos en hyperbolisk kaotisk spridare.

Fig. 8: Fyra medlemmar av den invarianta uppsättningen av Gaspard-Rice-systemet.

Fig. 9: Fyra medlemmar av den invarianta uppsättningen av Gaspard-Rice-systemet, itererade framåt i tiden.

Varje medlem av den invarianta uppsättningen kan modelleras med hjälp av symbolisk dynamik : banan är märkt baserat på var och en av skivorna från vilken den studsar. Uppsättningen av alla sådana sekvenser bildar en oräknelig uppsättning . För de fyra medlemmarna som visas i figurerna 8 och 9 kommer den symboliska dynamiken att vara följande:

...121212121212... ...232323232323... ...313131313131... ...123123123123...

Medlemmar av det stabila grenröret kan vara representerade på samma sätt, förutom att varje sekvens har en startpunkt. När du tänker på att en medlem av den invarianta uppsättningen måste "passa" i gränserna mellan två attraktionsbassänger, är det uppenbart att, om den störs, kan banan gå ut var som helst längs sekvensen. Således bör det också vara uppenbart att ett oändligt antal alternerande bassänger av alla tre "färger" kommer att finnas mellan varje given gräns.

På grund av deras instabila natur är det svårt att komma åt medlemmarna i den invarianta uppsättningen eller det stabila grenröret direkt. Osäkerhetsexponenten är idealiskt anpassad för att mäta fraktaldimensionen hos denna typ av system . Återigen genom att använda den enda effektparametern, b , utför vi flera försök med slumpmässiga påverkansparametrar, stör dem med en minut, $\epsilon$ , och räknar hur ofta antalet returer från skivorna ändras, det vill säga, osäkerhetsfraktionen. Observera att även om systemet är tvådimensionellt räcker det med en enda anslagsparameter för att mäta fraktaldimensionen hos det stabila grenröret. Detta visas i figur 10, som visar attraktionsbassängerna plottade som en funktion av en dubbel inverkansparameter, $\theta$ och $\phi$ . Det stabila grenröret, som kan ses i gränserna mellan bassängerna, är fraktal längs endast en dimension.

Fig. 10: Attraktionsbassängerna som en funktion av de dubbla påverkansparametrarna,

\theta

och

\phi

.

Figur 11 plottar osäkerhetsfraktionen, f , som en funktion av osäkerheten, $\epsilon$ för ett simulerat Gaspard–Rice-system. Lutningen på den anpassade kurvan returnerar osäkerhetsexponenten, ${\displaystyle \gamma =0,380} ,$ således är boxräknedimensionen för det stabila grenröret, $D_ {0}=N-\gamma =2-0,380=1,62$ . Den invarianta uppsättningen är skärningspunkten mellan de stabila och instabila grenrören .

Eftersom systemet är detsamma oavsett om det körs framåt eller bakåt, är det instabila grenröret helt enkelt spegelbilden av det stabila grenröret och deras fraktala dimensioner kommer att vara lika. På grundval av detta kan vi beräkna fraktaldimensionen för den invarianta mängden:

D=D_{s}+D_{u}-N=2D_{s}-N=N-2\gamma

där D_s och D_u är fraktaldimensionerna för de stabila respektive instabila grenrören och N =2 är systemets dimensionalitet. Den fraktala dimensionen för den invarianta mängden är D =1,24.

Fig. 10: Plott av osäkerhetsfraktionen för spridningssystemet Gaspard–Rice, med rak linjepassning, vilket ger osäkerhetsexponent .

Förhållandet mellan fraktaldimensionen, sönderfallshastighet och Lyapunov-exponenter

Från den föregående diskussionen borde det vara uppenbart att sönderfallshastigheten, fraktaldimensionen och Lyapunov-exponenterna alla är relaterade. Den stora Lyapunov-exponenten, till exempel, berättar hur snabbt en bana i den invarianta mängden kommer att divergera om den störs. På liknande sätt kommer fraktaldimensionen att ge oss information om tätheten av banor i den invarianta mängden. Således kan vi se att båda kommer att påverka sönderfallshastigheten som fångas i följande gissning för ett tvådimensionellt spridningssystem:

D_{1}=\left(h_{1}-{\frac {1}{\gamma }}\right)\ vänster({\frac {1}{h_{1}}}-{\frac {1}{h_{2}}}\right)

där D ₁ är informationsdimensionen och h ₁ och h ₂ är de små respektive stora Lyapunov-exponenterna. För en attraktion, $\gamma =\infty$ och det reduceras till Kaplan–Yorke-förmodan .

Se även

^ Gaspard, Pierre; Rice, Stuart A. (1989-02-15). "Skridning från en klassiskt kaotisk repeller". Journal of Chemical Physics . AIP-publicering. 90 (4): 2225–2241. doi : 10.1063/1.456017 . ISSN 0021-9606 .
^ ^a ^b ^c ^d ^e Edward Ott (1993). Kaos i dynamiska system . Cambridge University Press .
^ ^a ^b ^c Yalçinkaya, Tolga; Lai, Ying-Cheng (1995). "Kaotisk spridning" . Datorer i fysik . AIP-publicering. 9 (5): 511-518. doi : 10.1063/1.168549 . ISSN 0894-1866 .
^ ^a ^b ^c Peter Mills (2000). Ett experimentellt klassiskt kaotiskt spridningssystem undersökt (Teknisk rapport). University of Waterloo.
^ David Sweet, Edward Ott och James A. Yorke. "Komplex topologi i kaotisk spridning: en laboratorieobservation". Naturen . 399 :313.
^ ^a ^b Peter Mills (1998). Bullrig kaotisk spridning (avhandling). University of Waterloo.
^ Denny Gulick (1992). Möten med kaos . McGraw-Hill .
^ ^a ^b ^c Bleher, Siegfried; Grebogi, Celso ; Ott, Edward (1990). "Bifurkation till kaotisk spridning". Physica D: Icke-linjära fenomen . Elsevier BV. 46 (1): 87–121. doi : 10.1016/0167-2789(90)90114-5 . ISSN 0167-2789 .
^ Ott, Edward; Tél, Tamás (1993). "Kaotisk spridning: En introduktion" (PDF) . Kaos: En tvärvetenskaplig tidskrift för icke-linjär vetenskap . AIP-publicering. 3 (4): 417–426. doi : 10.1063/1.165949 . ISSN 1054-1500 . PMID 12780049 .

externa länkar

Programvara för simulering av Gaspard-Rice-systemet

[Gaspard_Rice1989-1] Gaspard, Pierre; Rice, Stuart A. (1989-02-15). "Skridning från en klassiskt kaotisk repeller". Journal of Chemical Physics . AIP-publicering. 90 (4): 2225–2241. doi : 10.1063/1.456017 . ISSN 0021-9606 .

[Ott1993-2] Edward Ott (1993). Kaos i dynamiska system . Cambridge University Press .

[Yalcinkaya_Lai1995-3] Yalçinkaya, Tolga; Lai, Ying-Cheng (1995). "Kaotisk spridning" . Datorer i fysik . AIP-publicering. 9 (5): 511-518. doi : 10.1063/1.168549 . ISSN 0894-1866 .

[Mills2000-4] Peter Mills (2000). Ett experimentellt klassiskt kaotiskt spridningssystem undersökt (Teknisk rapport). University of Waterloo.

[Sweet_etal1999-5] David Sweet, Edward Ott och James A. Yorke. "Komplex topologi i kaotisk spridning: en laboratorieobservation". Naturen . 399 :313.

[Mills1998-6] Peter Mills (1998). Bullrig kaotisk spridning (avhandling). University of Waterloo.

[Gulick1992-7] Denny Gulick (1992). Möten med kaos . McGraw-Hill .

[Bleher_etal1990-8] Bleher, Siegfried; Grebogi, Celso ; Ott, Edward (1990). "Bifurkation till kaotisk spridning". Physica D: Icke-linjära fenomen . Elsevier BV. 46 (1): 87–121. doi : 10.1016/0167-2789(90)90114-5 . ISSN 0167-2789 .

[Ott_Tel1993-9] Ott, Edward; Tél, Tamás (1993). "Kaotisk spridning: En introduktion" (PDF) . Kaos: En tvärvetenskaplig tidskrift för icke-linjär vetenskap . AIP-publicering. 3 (4): 417–426. doi : 10.1063/1.165949 . ISSN 1054-1500 . PMID 12780049 .