Kaotisk blandning

Ett exempel på kaotisk blandning

I kaosteori och vätskedynamik är kaotisk blandning en process genom vilken flödesspårare utvecklas till komplexa fraktaler under verkan av ett vätskeflöde . Flödet kännetecknas av en exponentiell tillväxt av vätskefilament. Även mycket enkla flöden, som den blinkande virveln, eller ändligt upplösta vindfält kan generera exceptionellt komplexa mönster från initialt enkla spårfält.

Fenomenet är fortfarande inte väl förstått och är föremål för mycket aktuell forskning.

Kontext av kaotisk advektion

Vätska flödar

Två grundläggande mekanismer är ansvariga för vätskeblandning : diffusion och advektion . I vätskor är enbart molekylär diffusion knappast effektiv för blandning. Advektion, det vill säga transport av materia genom ett flöde, krävs för bättre blandning.

Vätskeflödet lyder grundläggande ekvationer för vätskedynamik (som bevarande av massa och bevarande av momentum) som kallas Navier–Stokes ekvationer . Dessa ekvationer är skrivna för det Euleriska hastighetsfältet snarare än för vätskepartiklarnas lagrangiska position. Lagrangiska banor erhålls sedan genom att integrera flödet. Att studera effekten av advektion på vätskeblandning innebär att beskriva hur olika lagrangiska vätskepartiklar utforskar vätskeområdet och separerar från varandra.

Förutsättningar för kaotisk advektion

Ett vätskeflöde kan betraktas som ett dynamiskt system, det vill säga en uppsättning vanliga differentialekvationer som bestämmer utvecklingen av en lagrangisk bana . Dessa ekvationer kallas advektionsekvationer :

${\frac {d{\vec {x}}}{dt}}={\vec {v}}({\vec {x}} ,t)$

där ${\vec {v}}=(u,v,w)$ är komponenterna i hastighetsfältet, som antas vara kända från ekvationslösningen styr vätskeflödet, såsom Navier-Stokes ekvationer , och ${\vec {x}}=(x,y,z)$ är den fysiska positionen. Om det dynamiska systemet som styr banor är kaotiskt , är integrationen av en bana extremt känslig för initiala förhållanden, och närliggande punkter separeras exponentiellt med tiden. Detta fenomen kallas kaotisk advektion .

Dynamiska system och kaosteori säger att minst 3 frihetsgrader är nödvändiga för att ett dynamiskt system ska vara kaotiskt. Tredimensionella flöden har tre frihetsgrader motsvarande de tre koordinaterna, och resulterar vanligtvis i kaotisk advektion, förutom när flödet har symmetrier som minskar antalet frihetsgrader. I flöden med mindre än 3 frihetsgrader är lagrangiska banor begränsade till slutna rör, och skjuvningsinducerad blandning kan endast fortsätta inom dessa rör.

Detta är fallet för 2-D stationära flöden där det bara finns två frihetsgrader $x$ och $y$ . För stationära (tidsoberoende) flöden sammanfaller lagrangiska banor för vätskepartiklar med strömningslinjerna i flödet, det vill säga isoliner av strömfunktionen . I 2-D är strömlinjer koncentriska slutna kurvor som korsar endast vid stagnationspunkter . Således kan en fläck av färgad vätska som ska blandas endast utforska området som begränsas av den mest yttre och inre strömlinjen, på vilken den ligger vid den första tiden. När det gäller praktiska tillämpningar är denna konfiguration inte särskilt tillfredsställande.

För 2-D ostationära (tidsberoende) flöden sammanfaller inte längre momentana stängda strömlinjer och lagrangiska banor. Därför utforskar lagrangiska banor en större volym av volymen, vilket resulterar i bättre blandning. Kaotisk advektion observeras för de flesta 2-D ostationära flöden. Ett känt exempel är det blinkande virvelflödet som introducerades av Aref, där två fasta stavliknande omrörare växelvis roteras inuti vätskan. Att periodiskt byta den aktiva (roterande) omröraren introducerar ett tidsberoende i flödet, vilket resulterar i kaotisk advektion. Lagrangiska banor kan därför fly från slutna strömlinjer och besöka en stor del av vätskeområdet.

Klippa

Ett flöde främjar blandning genom att separera närliggande vätskepartiklar. Denna separation uppstår på grund av hastighetsgradienter , ett fenomen som kallas skjuvning . Låt ${\vec {x}}_{1}$ och ${\vec {x}}_{2}$ vara två angränsande vätskepartiklar, åtskilda av $\delta {\vec {x}}={\vec {x}}_{2}-{\vec {x}}_{1}$ vid tidpunkten t . När partiklarna advekeras av ett flöde ${\vec {v}}$ , vid tiden $t+\delta t$ kan den ungefärliga separationen mellan partiklarna hittas genom Taylor-expansion :

${\frac {\mathrm {d} }{\mathrm {d} t}}({\vec {x }}+\delta {\vec {x}})\approx {\vec {v}}+\nabla {\vec {v}}\cdot \delta {\vec {x}}$

därav

$\delta x(t+\delta t)\approx \delta x(t)+\delta t( \delta x\cdot \nabla ){\vec {v}}$

och

${\frac {\mathrm {d} }{\mathrm {d} t}}\delta {\vec {x}}\approx \nabla { \vec {v}}\cdot \delta {\vec {x}}$

Tillväxthastigheten för separationen ges därför av gradienten för hastighetsfältet i separationsriktningen. Det plana skjuvflödet är ett enkelt exempel på storskaligt stationärt flöde som deformerar vätskeelement på grund av en enhetlig skjuvning.

Karakterisering av kaotisk advektion

Lyapunov exponenter

Om flödet är kaotiskt kommer små initiala fel, ${\displaystyle \delta {\vec {x}}},$ i en bana att divergera exponentiellt. Vi är intresserade av att beräkna stabiliteten – dvs hur snabbt divergerar närliggande banor? Jacobi -matrisen för hastighetsfältet, ${\displaystyle \nabla {\vec {v}}} ,$ ger information om den lokala divergenshastigheten för närliggande banor eller den lokala sträckningshastigheten för lagrangeutrymmet .

Vi definierar matrisen H så att:

${\frac {\mathrm {d} }{\mathrm {d} t}}{\boldsymbol {H}}\equiv \ nabla {\vec {v}}\cdot {\boldsymbol {H}},\qquad {\boldsymbol {H}}(t=0)={\boldsymbol {I}}$

där I är identitetsmatrisen. Det följer att:

$\delta {\vec {x}}(t)\approx {\boldsymbol {H}}\cdot \delta {\vec {x}}_{0 }$

Lyapunov -exponenterna med ändlig tid definieras som tidsgenomsnittet av logaritmerna av längderna av huvudkomponenterna i vektorn H under en tid t:

${\boldsymbol {H^{T}}}\cdot {\boldsymbol {H}}\cdot \delta {\vec {x} }_{0i}=h_{i}\cdot \delta {\vec {x}}_{0i}$

$\ displaystyle \lambda _{i}({\vec {x}},t)\equiv {\frac {1}{2t}}\ln {h_{i}({\vec {x}},t)}}$

där $\lambda _{i}({\vec {x}},t)\geq \lambda _{i+1} ({\vec {x}},t)$ är den i: te Lyapunov-exponenten i systemet, medan $\delta {\vec {x}}_{0i}$ är den i: te huvudkomponenten av matrisen H .

Om vi ​​börjar med en uppsättning ortonormala initiala felvektorer, $\{\delta {\vec {x}}_{0i}\}$ så kommer matrisen H att mappa dem till en uppsättning av slutliga ortogonala felvektorer av längden $\{{\sqrt {h_{i}({\vec {x}},t)}}\}$ . Systemets åtgärd mappar en infinitesimal sfär av initialpunkter till en ellipsoid vars huvudaxel ges av ${\sqrt {h_{1}({\vec {x}}, t)}}$ medan biaxeln ges av ${\displaystyle {\sqrt {h_{N}({\vec {x}},t)}}} ,$ där N är antal dimensioner.

Denna definition av Lyapunov-exponenter är både mer elegant och mer lämplig för dynamiska system i verkliga världen än den mer vanliga definitionen baserad på diskreta funktionskartor. Kaos definieras som förekomsten av minst en positiv Lyapunov-exponent.

I ett kaotiskt system kallar vi Lyapunov-exponenten för det asymptotiska värdet av det största egenvärdet av H :

$\lambda =\lim _{t\to \infty }\lambda _{1}({\vec {x}},t)$

Om det finns någon signifikant skillnad mellan Lyapunov-exponenterna, då en felvektor utvecklas framåt i tiden, kommer varje förskjutning i riktningen för den största tillväxten att tendera att förstoras. Således:

$|\delta {\vec {x}}|\approx |\delta {\vec {x}}_{0}|e^{\lambda _{1}t}.$

Lyapunov-exponenten för ett flöde är en unik kvantitet som kännetecknar den asymptotiska separationen av vätskepartiklar i ett givet flöde. Det används ofta som ett mått på effektiviteten av blandning, eftersom det mäter hur snabbt banor separeras från varandra på grund av kaotisk advektion. Lyapunov-exponenten kan beräknas med olika metoder:

• genom att följa en enda bana under mycket långa tider och beräkna $\lambda =\lim _{t\to \infty }\lambda _{1}({\ vec {x}},t)$ .
• eller genom att följa en ensemble av banor under en given tidsperiod och beräkna ensemblens medelvärde: $<\lambda >_{trajectories}$

Likvärdigheten mellan de två metoderna beror på det kaotiska systemets ergodicitet .

Filamenttillväxt kontra utveckling av spårämnesgradienten

Följande exakta ekvation kan härledas från en advektions-diffusionsekvation (se nedan), med en diffusionsterm ( D=0 ) på noll:

${\frac {\mathrm {d} \nabla q}{\mathrm {d} t}}=-\nabla q\cdot \nabla {\vec {v}}$

Parallellt med definitionen av Lyapunov-exponenten definierar vi matrisen ${\boldsymbol {H}}^{\prime }$ , enligt följande:

${\frac {\mathrm {d} {\boldsymbol {H^{\prime }}}}{\mathrm {d} t}}=-\nabla {\boldsymbol {H^{\prime }}}\cdot \nabla {\vec {v}}\qquad {\boldsymbol {H^{\prime }}}(t= 0)={\boldsymbol {I}}$

Det är lätt att visa att:

${\boldsymbol {H^{\prime }}}={\boldsymbol {H}}^{-1}$

Om vi ​​definierar $\lbrace h_{i}^{\prime }\rbrace$ som de kvadratiska längderna av huvudkomponenterna i spårningsgradientmatrisen, ${\boldsymbol {H} }^{\prime }$ , sedan:

$h_{i}^{\prime }=1/h_{i}$

där $\lbrace h_{i}^{\prime }\rbrace$ är ordnade, som tidigare, från största till minsta. Därför kommer tillväxt i felvektorn att orsaka en motsvarande minskning av spårämnesgradienten och vice versa. Detta kan förstås mycket enkelt och intuitivt genom att beakta två närliggande punkter: eftersom skillnaden i spårämneskoncentration kommer att vara fixerad, kommer den enda källan till variation i gradienterna mellan dem att vara deras separation.

Konturadvektion

Utveckling av en advekerad kontur

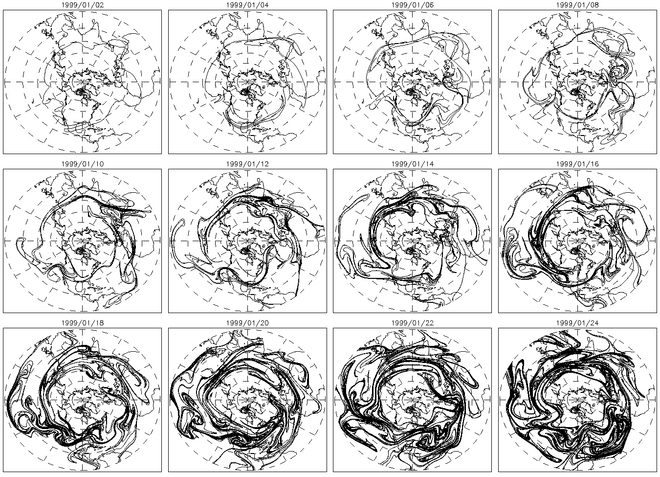
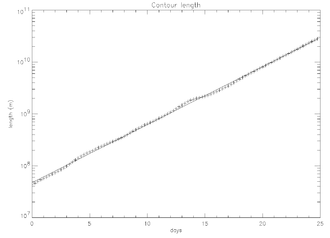
Konturadvektion är en annan användbar metod för att karakterisera kaotisk blandning. I kaotiska flöden kommer adverade konturer att växa exponentiellt över tiden. Figuren ovan visar utvecklingen bildruta för bildruta av en kontur advektionerad under flera dagar. Figuren till höger visar längden på denna kontur som funktion av tiden.

Tillväxt av advekerad kontur

Kopplingen mellan exponentiell konturtillväxt och positiva Lyapunov-exponenter är lätt att se. Hastigheten för konturtillväxt ges som:

${\frac {\mathrm {d} L}{\mathrm {d} t}}=\int |\nabla {\vec {v}}\cdot \mathrm {d} {\vec {s}} |$

där $\mathrm {d} {\vec {s}}$ är banan och integralen utförs över konturens längd. Konturtillväxthastigheten kommer att approximera genomsnittet av de stora Lyapunov-exponenterna:

$L\approx L_{0}\exp({\bar {\lambda }}_{1}t)$

Poincaré-sektioner

I kaotisk advektion färdas en vätskepartikel inom ett stort område och möter andra partiklar som från början var långt ifrån den. Man kan då anse att en partikel är blandad med partiklar som färdas inom samma region. Den region som täcks av en bana spänner dock inte alltid över hela vätskedomänen. Poincaré-sektioner används för att skilja regioner med bra och dålig blandning.

Poincaré-kartan definieras som transformationen

${\begin{aligned}{\boldsymbol {M}}\colon {\vec {x_{i}}}(t_{i})&\to {\vec {x}}_{i+1} (t_{i+1}=t_{i}+T,{\vec {x_{i}}}).\end{aligned}}$

${\boldsymbol {M}}$ omvandlar en punktliknande partikel till partikelns position efter ett tidsintervall T. Speciellt för ett tidsperiodiskt flöde med period T, applicering av kartan flera gånger på en partikel ger de successiva positionerna för partikeln period efter period. En Poincaré-sektion byggs genom att utgå från några olika initiala förhållanden och plotta motsvarande iterater. Detta handlar om att plotta banorna med stroboskop för varje T.

Som ett exempel visar figuren som presenteras här (vänster del) Poincaré-sektionen som erhålls när man periodvis applicerar en åtta-liknande rörelse på en cirkulär blandningsstav. Vissa banor sträcker sig över ett stort område: detta är det kaotiska eller blandningsområdet, där bra blandning sker. Men det finns också två "hål": i dessa regioner är banorna stängda. Dessa kallas elliptiska öar, eftersom banorna inuti är elliptiska kurvor. Dessa områden är inte blandade med resten av vätskan. För blandningsapplikationer måste elliptiska öar undvikas av två skäl:

• Vätskepartiklar kan inte passera öarnas gränser (förutom genom långsam diffusion), vilket resulterar i segregation.
• Att blanda inuti dessa regioner är inte effektivt eftersom banorna är stängda och därför inte kaotiska.

Att undvika icke-kaotiska öar kräver förståelse för dessa regioners fysiska ursprung. Generellt sett kan en förändring av flödets geometri ändra närvaron eller frånvaron av öar. I flödet av åtta siffror, till exempel, för en mycket tunn stav, känns stavens inflytande inte långt från sin plats, och nästan cirkulära banor finns inom öglorna i åttasiffran. Med en större stav (högra delen av figuren) kan partiklar fly från dessa slingor och öar finns inte längre, vilket resulterar i bättre blandning.

Med en Poincaré-sektion kan blandningskvaliteten hos ett flöde analyseras genom att skilja mellan kaotiska och elliptiska regioner. Detta är emellertid ett grovt mått på blandningsprocessen, eftersom sträckningsegenskaperna inte kan härledas från denna kartläggningsmetod. Ändå är denna teknik mycket användbar för att studera blandningen av periodiska flöden och kan utökas till en 3D-domän.

Fraktal dimension

Genom en kontinuerlig process av sträckning och vikning, ungefär som i en " bakarkarta ", kommer spårämnen som förekommer i kaotiska flöden att utvecklas till komplexa fraktaler. Den fraktala dimensionen för en enskild kontur kommer att vara mellan 1 och 2. Exponentiell tillväxt säkerställer att konturen, inom gränsen för mycket lång tids integration, blir fraktal. Fraktaler som består av en enda kurva är oändligt långa och när de bildas iterativt har de en exponentiell tillväxthastighet, precis som en advekerad kontur. Koch Snowflake , till exempel, växer med en hastighet av 4/3 per iteration.

Figuren nedan visar fraktaldimensionen av en advekerad kontur som funktion av tiden, mätt på fyra olika sätt. En bra metod för att mäta fraktaldimensionen av en adverad kontur är osäkerhetsexponenten .

Advected kontur fraktal dimension

Utveckling av spårkoncentrationsfält i kaotisk advektion

Vid vätskeblandning vill man ofta homogenisera en art, som kan karakteriseras av dess koncentrationsfält q . Ofta kan arten betraktas som ett passivt spårämne som inte ändrar flödet. Arten kan till exempel vara ett färgämne som ska blandas. Utvecklingen av ett koncentrationsfält $q$ följer advektion-diffusionsekvationen , även kallad konvektion-diffusionsekvation :

${\big .}{\frac {\partial q}{\partial t}}=\nabla \cdot D\nabla q-{\vec {v}}\cdot \nabla q.$

Jämfört med den enkla diffusionsekvationen representerar termen proportionell mot hastighetsfältet ${\vec {v}}$ effekten av advektion.

Vid blandning av en spårämnesfläck dominerar advektionstermen utvecklingen av koncentrationsfältet i början av blandningsprocessen. Kaotisk advektion förvandlar fläcken till ett knippe av tunna filament. Bredden på ett färgämnesfilament minskar exponentiellt med tiden, tills en jämviktsskala uppnås, vid vilken diffusionseffekten börjar bli signifikant. Denna skala kallas för Batchelor-skalan . Den definieras som kvadratroten av förhållandet mellan diffusionskoefficienten och Lyapunov-exponenten

$w_{B}={\sqrt {\frac {D}{\lambda }}}$

där $\lambda$ är Lyapunov-exponenten och D är diffusionskoefficienten. Denna skala mäter balansen mellan sträckning och diffusion på utvecklingen av koncentrationsfältet: sträckning tenderar att minska bredden på en filament, medan diffusion tenderar att öka den. Batchelor-skalan är den minsta längdskalan som kan observeras i koncentrationsfältet, eftersom diffusion snabbt smetar ut alla finare detaljer.

När de flesta färgfilament når Batchelor-skalan, börjar diffusionen avsevärt minska kontrasten mellan koncentrationen mellan filamentet och den omgivande domänen. Tidpunkten då ett glödtråd når Batchelor-skalan kallas därför dess blandningstid. Upplösningen av advektion-diffusionsekvationen visar att efter blandningstiden för ett filament är minskningen av koncentrationsfluktuationen på grund av diffusion exponentiell, vilket resulterar i snabb homogenisering med den omgivande vätskan.

Historia om kaotisk advektion

Födelsen av teorin om kaotisk advektion spåras vanligtvis tillbaka till en artikel från 1984 av Hassan Aref . I detta arbete studerade Aref blandningen som inducerades av två virvlar som växlade till och från inuti en inviscid vätska . Detta avgörande arbete hade möjliggjorts av tidigare utvecklingar inom områdena dynamiska system och vätskemekanik under de föregående decennierna. Vladimir Arnold och Michel Hénon hade redan märkt att de banor som avser områdesbevarande tredimensionella flöden kunde vara kaotiska. Det praktiska intresset av kaotisk advektion för vätskeblandningstillämpningar förblev dock obemärkt fram till Arefs arbete på 80-talet. Sedan dess har hela verktygslådan av dynamiska system och kaosteori använts för att karakterisera vätskeblandning genom kaotisk advektion. Senare arbete har till exempel använt topologiska metoder för att karakterisera sträckningen av vätskepartiklar. Andra nya forskningsriktningar gäller studiet av kaotisk advektion i komplexa flöden, såsom granulära flöden.

externa länkar

• ctraj : Verktyg för att studera kaotisk advektion.