Kamfilter

Frammatning av kamfilterstruktur

Vid signalbehandling är ett kamfilter ett filter som implementeras genom att lägga till en fördröjd version av en signal till sig själv, vilket orsakar konstruktiv och destruktiv störning . Frekvenssvaret en serie regelbundet åtskilda skåror mellan regelbundet åtskilda toppar (kallas ibland tänder ) som ger utseendet av en kam .

Ansökningar

Advanced PAL Comb Filter-II (APCF-II, Motorola MC141627FT)

Kamfilter används i en mängd olika signalbehandlingstillämpningar, inklusive:

• Cascaded integrator-comb (CIC)-filter, som vanligtvis används för kantutjämning under interpolations- och decimeringsoperationer som ändrar samplingshastigheten för ett tidsdiskret system.
• 2D- och 3D-kamfilter implementerade i hårdvara (och ibland mjukvara) i analoga PAL- och NTSC- tv-avkodare, minskar artefakter som punktgenomsökning .
• Ljudsignalbehandling , inklusive fördröjning , flänsning , fysisk modelleringsyntes och digital vågledarsyntes . Om fördröjningen är inställd på några millisekunder kan ett kamfilter modellera effekten av akustiska stående vågor i en cylindrisk kavitet eller i en vibrerande sträng .
• Inom astronomi lovar astro-kammen att öka precisionen hos befintliga spektrografer med nästan hundra gånger.

Inom akustik kan kamfiltrering uppstå som en oönskad artefakt. Till exempel skapar två högtalare som spelar samma signal på olika avstånd från lyssnaren en kamfiltrerande effekt på ljudet. I alla slutna utrymmen hör lyssnarna en blandning av direkt ljud och reflekterat ljud. Det reflekterade ljudet tar en längre, fördröjd väg jämfört med det direkta ljudet, och ett kamfilter skapas där de två blandas hos lyssnaren.

Genomförande

Kamfilter finns i två former, feedforward och feedback ; som hänvisar till i vilken riktning signaler fördröjs innan de läggs till ingången.

Kamfilter kan implementeras i tidsdiskreta eller kontinuerliga tidsformer som är mycket lika.

Formulär för feedforward

Frammatning av kamfilterstruktur

Den allmänna strukturen för ett framkopplat kamfilter beskrivs av differensekvationen :

$y[n]=x[n]+\alpha x[nK]$

där $K$ är fördröjningslängden (mätt i sampel), och α är en skalningsfaktor som appliceras på den fördröjda signalen. Z - transformen av båda sidor av ekvationen ger:

$Y(z)=\left(1+\alpha z^{-K}\right)X(z)$

Överföringsfunktionen definieras som :

$H(z)={\frac {Y(z)}{X(z)} }=1+\alpha z^{-K}={\frac {z^{K}+\alpha }{z^{K}}}$

Frekvenssvar

Återkopplad storlekssvar för olika positiva värden på α och K = 1

Framkopplingsstorlekssvar för olika negativa värden på α och K = 1

Frekvenssvaret för ett diskret tidssystem uttryckt i z-domänen erhålls genom substitution z = ejΩ ^. Därför, för framkopplade kamfiltret:

$H\left(e^{j\Omega }\right)=1+\alpha e^{-j\Omega K}$

Med Eulers formel ges frekvenssvaret också av

$H\left(e^{j\Omega }\right)={\bigl [} 1+\alpha \cos(\Omega K){\bigr ]}-j\alpha \sin(\Omega K)$

Ofta av intresse är storlekssvaret , som ignorerar fasen. Detta definieras som:

$\left|H\left(e^{j\Omega }\right)\right|={\sqrt { \Re \left\{H\left(e^{j\Omega}\right)\right\}^{2}+\Im \left\{H\left(e^{j\Omega}\right)\ höger\}^{2}}}$

I fallet med framkopplat kamfilter är detta:

$\left|H\left(e^{j\Omega }\right)\right|={\sqrt {\left(1+\ alpha ^{2}\right)+2\alpha \cos(\Omega K)}}$

Termen (1 + α ² ) är konstant, medan 2 α cos( ΩK ) termen varierar periodiskt . Följaktligen är kamfiltrets storlekssvar periodisk.

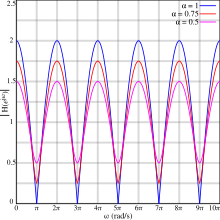
Graferna visar storlekssvaret för olika värden på α , vilket visar denna periodicitet. Några viktiga egenskaper:

• Svaret sjunker med jämna mellanrum till ett lokalt minimum (ibland känt som en skåra ), och stiger periodvis till ett lokalt maximum (ibland känt som en topp eller en tand ).
• För positiva värden på α inträffar det första minimum vid halva fördröjningsperioden och upprepas med jämna multiplar av fördröjningsfrekvensen därefter:

$f={\frac {1}{2K}},{\frac {3}{2K}},{\frac {5}{2K} }\cdots$ .

• Nivåerna för maxima och minima är alltid på samma avstånd från 1.
• När α = ±1 har minima noll amplitud. I det här fallet kallas minima ibland som nollor .
• Maxima för positiva värden på α sammanfaller med minima för negativa värden för ${\displaystyle \alpha } ,$ och vice versa.

Impulsivt svar

Forward-kamfiltret är ett av de enklaste finita impulssvarsfiltren . Dess svar är helt enkelt den initiala impulsen med en andra impuls efter fördröjningen.

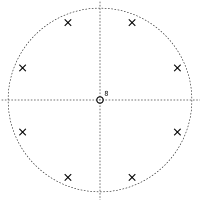
Pole-noll tolkning

Titta igen på z -domänöverföringsfunktionen för feedforward kamfiltret:

$H(z)={\frac {z^{K}+\alpha }{z^{K}}}$

täljaren är lika med noll när z ^K = − α . Detta har K lösningar, lika fördelade runt en cirkel i det komplexa planet ; dessa är nollorna för överföringsfunktionen. Nämnaren är noll vid z ^K = 0 , vilket ger K poler vid z = 0 . Detta leder till en pol-noll-plot som de som visas.

Pol-noll plot av framkopplat kamfilter med K = 8 och α = 0,5

Pol-noll plot av framkopplat kamfilter med K = 8 och α = −0,5

Återkopplingsformulär

Återkopplingskamfilterstruktur

På liknande sätt beskrivs den allmänna strukturen för ett återkopplingskamfilter av differensekvationen :

$y[n]=x[n]+\alpha y[nK]$

Denna ekvation kan arrangeras om så att alla termer i $y$ är på vänster sida, och sedan ta z - transformen:

$\left(1-\alpha z^{-K}\right)Y(z)=X(z)$

Överföringsfunktionen är därför:

$H(z)={\frac {Y(z)}{X(z) }}={\frac {1}{1-\alpha z^{-K}}}={\frac {z^{K}}{z^{K}-\alpha }}$

Frekvenssvar

Återkopplingsstorlekssvar för olika positiva värden på α och K = 2

Återkopplingsstorlekssvar för olika negativa värden på α och K = 2

Genom att ersätta z = e ^jΩ i z -domänuttrycket för återkopplingskamfiltret:

$H\left(e^{j\Omega }\right)={\frac {1}{1-\alpha e^{-j \Omega K}}}$

Storlekssvaret är som följer:

$\left|H\left(e^{j\Omega}\right)\right|={\frac {1}{\sqrt {\left(1+\alpha ^{2}\right)-2\alpha \cos(\Omega K)}}}$

Återigen är svaret periodiskt, vilket graferna visar. Återkopplingskamfiltret har några egenskaper gemensamma med feedforward-formuläret:

• Svaret sjunker periodvis till ett lokalt minimum och stiger till ett lokalt maximum.
• Maxima för positiva värden på α sammanfaller med minima för negativa värden för ${\displaystyle \alpha } ,$ och vice versa.
• För positiva värden på α inträffar det första maximum vid 0 och upprepas med jämna multiplar av fördröjningsfrekvensen därefter:

$f=0,{\frac {1}{K}},{\frac {2}{K}},{\frac {3}{K} }\cdots$ .

Men det finns också några viktiga skillnader eftersom storlekssvaret har en term i nämnaren :

• samma avstånd från 1. Maxima har en amplitud på 1/1 − α .
• Filtret är bara stabilt om | α | är strikt mindre än 1. Som framgår av graferna, som | α | ökar, stiger maximans amplitud allt snabbare.

Impulsivt svar

Återkopplingskamfiltret är en enkel typ av oändligt impulssvarsfilter . Om det är stabilt består svaret helt enkelt av en upprepad serie impulser som minskar i amplitud med tiden.

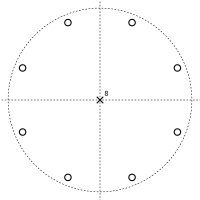
Pole-noll tolkning

Titta igen på z -domänöverföringsfunktionen för återkopplingskamfiltret:

$H(z)={\frac {z^{K}}{z^{K}-\alpha }}$

Den här gången är täljaren noll vid z ^K = 0 , vilket ger K nollor vid z = 0 . Nämnaren är lika med noll när z ^K = α . Detta har K lösningar, lika fördelade runt en cirkel i det komplexa planet ; dessa är polerna för överföringsfunktionen. Detta leder till en pol-noll-plot som de som visas nedan.

Pol-noll plot av återkopplingskamfilter med K = 8 och α = 0,5

Pol-noll plot av återkopplingskamfilter med K = 8 och α = −0,5

Kontinuerliga kamfilter

Kamfilter kan också implementeras i kontinuerlig tid . Forward-formen kan beskrivas med ekvationen:

$y(t)=x(t)+\alpha x(t-\tau )$

där τ är fördröjningen (mätt i sekunder). Denna har följande överföringsfunktion:

$H(s)=1+\alpha e^{-s\tau }$

Forward-formen består av ett oändligt antal nollor fördelade längs jω-axeln.

Feedbackformuläret har ekvationen:

$y(t)=x(t)+\alpha y(t-\tau )$

och följande överföringsfunktion:

$H(s)={\frac {1}{1-\alpha e^{-s\tau }}}$

Återkopplingsformen består av ett oändligt antal poler fördelade längs jω-axeln.

Implementeringar i kontinuerlig tid delar alla egenskaper hos respektive tidsdiskreta implementeringar.

Se även

• Dirac kam
• Fabry–Pérot interferometer

externa länkar

• Media relaterade till Comb-filter på Wikimedia Commons