Jeep problem

Plott över mängden bränsle f mot avståndet från utgångspunkt d för att utforska (1–3) och korsande (I–III) versioner av jeepproblemet för tre enheter bränsle – färgade pilar anger depåer, diagonala segment anger färd och vertikala segment anger bränsle överföra

Jeepproblemet , ökenkorsningsproblemet eller prospekteringsproblemet är ett matematiskt problem där en jeep måste maximera sträckan den kan färdas in i en öken med en given mängd bränsle. Jeepen kan bara bära en fast och begränsad mängd bränsle, men den kan lämna bränsle och samla bränsle vid bränsledeponier var som helst i öknen.

Problemet dök först upp i 800-talssamlingen Propositiones ad Acuendos Juvenes ( Problem för att skärpa de unga ), som tillskrivs Alcuin , där pusslet handlar om en resande kamel som äter säd. De viribus quantitatis (ca 1500) av Luca Pacioli diskuterar också problemet. En modern behandling gavs av NJ Fine 1947.

Variationer av problemet är kamel- och bananproblemet där en handlare måste maximera antalet bananer som transporteras till en marknad med hjälp av en kamel som livnär sig på bananerna, resenärerna över öknenproblemet där ett antal resenärer alla måste nå en destination och kan byter bara förnödenheter istället för att lämna dem, och bilarna över öknenproblemet som återigen bara kan byta ut sitt bränsle, men där tomma bilar kan överges. Detta sista problem har likheter med driften av flerstegsraketer .

Problem

Rita efter skala för Exploring (överst) och Crossing (nederst) versionerna av jeepproblemet för tre enheter bränsle. Den horisontella axeln anger avstånd och den vertikala axeln anger tid. Vertikala färgade linjesegment betecknar lagring av bränsle och horisontella anger färd med uttaget bränsle. Färgade siffror anger enheter av bränsle som gömts i det ögonblicket.

Det finns n enheter bränsle som lagras på en fast bas. Jeepen kan bära högst 1 enhet bränsle när som helst, och kan färdas 1 enhet av sträcka på 1 enhet bränsle (jeepens bränsleförbrukning antas vara konstant). När som helst under en resa kan jeepen lämna vilken mängd bränsle som helst som den bär på en bränsledeponi, eller kan samla in vilken mängd bränsle som helst som lämnades kvar på en bränsledeponi på en tidigare resa, så länge som dess bränslebelastning aldrig överstiger 1 enhet. Det finns två varianter av problemet:

Utforska öknen - jeepen måste återvända till basen i slutet av varje resa.
Att korsa öknen – jeepen måste återvända till basen i slutet av varje resa utom för den sista resan, då jeepen färdas så långt den kan innan den får slut på bränsle.

I båda fallen är målet att maximera den sträcka som jeepen tillryggalägger på sin sista resa. Alternativt kan målet vara att hitta den minsta mängd bränsle som krävs för att producera en sista resa på en given sträcka.

Variationer

I det klassiska problemet behandlas bränslet i jeepen och vid bränsledumpar som en kontinuerlig mängd. Mer komplexa varianter av problemet har föreslagits där bränslet endast kan lämnas eller samlas upp i diskreta mängder.

I kamel- och bananproblemet har handlaren n enheter bananer. Kamelen kan bära högst 1 enhet bananer när som helst och kan resa 1 enhet av avstånd på 1 enhet bananer. Marknaden är på m enheter avstånd bort. När som helst under en resa kan kamelen lämna vilken mängd bananer som helst som den bär på en lägerpost, eller kan den samla vilken mängd bananer som helst som lämnades kvar på en lägerpost på en tidigare resa, så länge som dess bananbelastning aldrig överstiger 1 enhet. Problemet kräver det maximala antalet bananer som kan transporteras till marknaden.

I resenärerna över öknenproblemet har startbasen obegränsade enheter av förnödenheter. Varje resenär kan ta med sig högst 1 enhet förnödenheter när som helst och kan resa 1 enhet av avstånd på en enhet förnödenheter. Den andra basen är på m enheter av avstånd bort. I motsats till de två föregående problemen kan resenärerna inte lämna förnödenheter i öknen; Men när som helst under en resa kan medföljande resenärer överföra förnödenheter sinsemellan, så länge som varje resenär aldrig har med sig mer än en enhet av förnödenheter. Varje återkommande resenär måste ha tillräckligt med förnödenheter på vägen tillbaka. Problemet kräver det minsta antal medföljande resenärer som behövs för att nå den andra basen. En variant av detta problem ger det totala antalet tillgängliga resenärer och frågar efter det maximala avståndet som kan nås.

I bilarna över ökenproblemet har startbasen obegränsade enheter bränsle. Varje bil kan bära högst 1 enhet förnödenheter när som helst och kan färdas 1 enhet av sträcka på 1 enhet bränsle. Den andra basen är på m enheter av avstånd bort. Bilarna kan inte lämna bränsle i öknen; Men när som helst under en resa kan följebilar överföra bränsle sinsemellan, så länge varje bil aldrig bär mer än 1 enhet bränsle. Tomma bilar utan bränsle är övergivna i öknen. Problemet kräver det minsta antal följebilar som behövs för att nå den andra basen. En variant av detta problem ger det totala antalet tillgängliga bilar och frågar efter det maximala avståndet som kan nås.

Lösning

Lösning på varianten "utforska öknen" för n = 3, som visar bränsleinnehållet i jeep och bränsledumpar vid början av varje resa och vid vändpunkten på varje resa.

En strategi som maximerar det tillryggalagda avståndet på den sista resan för varianten "Utforska öknen" är följande:

Jeepen gör n turer. På varje resa startar den från basen med 1 enhet bränsle.
På den första resan färdas jeepen en sträcka på 1/(2 n ) enheter och lämnar ( n − 1)/ n enheter bränsle vid en bränsledeponi. Jeepen har fortfarande 1/(2 n ) enheter bränsle – precis tillräckligt för att återvända till basen.
På var och en av de efterföljande n − 1 turerna samlar jeepen 1/(2 n ) enheter bränsle från denna första bränsledump på vägen ut, så att den lämnar bränsledumpen med 1 enhet bränsle. Den samlar också in 1/(2 n ) enheter bränsle från denna första bränsledump på vägen tillbaka, vilket är precis tillräckligt med bränsle för att återvända till basen.
På den andra resan åker jeepen till den första bränsledumpen och tankar. Den färdas sedan en sträcka på 1/(2 n − 2) enheter och lämnar ( n − 2)/( n − 1) enheter bränsle vid en andra bränsledump. Jeepen har fortfarande 1/(2 n − 2) enheter bränsle, vilket är precis tillräckligt för att återvända till den första bränsledumpen. Här samlar den in 1/(2 n ) enheter bränsle, vilket är precis tillräckligt med bränsle för att återgå till basen.
På var och en av de efterföljande n − 2 turerna samlar jeepen 1/(2 n − 2) enheter bränsle från denna andra bränsledump på vägen ut, så att den lämnar bränsledumpen med 1 enhet bränsle. Den samlar också upp 1/(2 n − 2) enheter bränsle från den andra bränsledumpen på vägen tillbaka, vilket är precis tillräckligt med bränsle för att återgå till den första bränsledumpen.
Jeepen fortsätter på detta sätt, så att den på resa k etablerar en ny k: te bränsledump på ett avstånd av 1/(2 n − 2 k + 2) enheter från föregående bränsledump och lämnar ( n − k )/( n − k + 1) enheter bränsle där. På var och en av de efterföljande n − k turerna samlar den upp 1/(2 n − 2 k + 2) enheter bränsle från den k: te tippen på väg ut och ytterligare 1/(2 n − 2 k + 2) enheter bränsle på väg tillbaka.

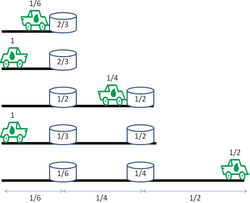
När jeepen börjar sin sista resa finns det n − 1 bränsledumpar. Den längst bort innehåller 1/2 av en enhet bränsle, den näst längsta innehåller 1/3 av en enhet bränsle, och så vidare, och den närmaste bränsledumpen har bara 1/ n enheter bränsle kvar. Tillsammans med 1 enhet bränsle som den startar från basen innebär detta att jeepen kan färdas en total tur-retur sträcka på

1+{\frac {1}{2}}+{ \frac {1}{3}}+\cdots +{\frac {1}{n}}=\sum _{k=1}^{n}{\frac {1}{k}}\equiv 2\ gånger \mathrm {utforska} (n)

enheter på sin sista resa (den maximala sträckan in i öknen är hälften av detta). Den samlar upp hälften av det återstående bränslet vid varje soptipp på vägen ut, vilket fyller dess tank. Efter att ha lämnat det längsta bort bränsletuppet färdas den 1/2 enhet längre in i öknen och återvänder sedan till den längsta bränsledumpen. Den samlar upp det återstående bränslet från varje bränsledump på vägen tillbaka, vilket precis räcker för att nå nästa bränsledump eller, i det sista steget, för att återvända till basen.

Lösning på varianten "korsa öknen" för n = 3, som visar bränsleinnehållet i jeep och bränsledumpar vid början av varje resa, vid vändpunkten på de två första turerna och i slutet av den sista resan.

Den sträcka som tillryggalagts på den sista resan är det n _: te övertonstalet , Hn . Eftersom övertonstalen är obegränsade är det möjligt att överskrida vilket givet avstånd som helst på den sista resan, så länge som tillräckligt med bränsle finns tillgängligt vid basen. Men både mängden bränsle som krävs och antalet bränsledumpar ökar exponentiellt med avståndet som ska tillryggaläggas.

Varianten "crossing the desert" kan lösas med en liknande strategi, förutom att det nu inte finns något krav på att hämta bränsle på vägen tillbaka på sista resan. Så på resa k etablerar jeepen en ny k: te bränsledump på ett avstånd av 1/(2 n − 2 k + 1) enheter från föregående bränsledump och lämnar (2 n − 2 k − 1)/(2 n − 2 k + 1) enheter bränsle där. På var och en av de nästa n − k − 1 turerna samlar den upp 1/(2 n − 2 k + 1) enheter bränsle från den k: te tippen på väg ut och ytterligare 1/(2 n − 2 k + 1) enheter bränsle på väg tillbaka.

Nu när jeepen börjar sin sista resa finns det n − 1 bränsledumpar. Den längst bort innehåller 1/3 av en enhet bränsle, den näst längsta innehåller 1/5 av en enhet bränsle, och så vidare, och den närmaste bränsledumpen har bara 1/(2 n − 1) enheter bränsle kvar. Tillsammans med 1 enhet bränsle som den startar med från basen innebär detta att jeepen kan färdas en total sträcka på

{\ displaystyle 1+{\frac {1}{3}}+{\frac {1}{5}}+\cdots +{\frac {1}{2n-1}}=\summa _{k=1}^ {n}{\frac {1}{2k-1}}=H_{2n-1}-{\frac {1}{2}}H_{n-1}\equiv \mathrm {cross} (n)}

enheter på sin sista resa. Den samlar upp allt återstående bränsle vid varje soptipp på vägen ut, vilket fyller dess tank. Efter att ha lämnat det längsta bort bränsletuppet färdas den ytterligare en sträcka på 1 enhet.

Anteckna det

\mathrm { cross} (n)=\summa _{k=1}^{n}{\frac {1}{2k-1}}>\summa _{k=1}^{n}{\frac {1}{ 2k}}={\frac {1}{2}}H_{n}=\mathrm {utforska} (n)

så det är i teorin möjligt att korsa en öken av vilken storlek som helst med tillräckligt med bränsle vid basen. Liksom tidigare ökar både mängden bränsle som krävs och antalet bränsledumpar exponentiellt med avståndet som ska tillryggaläggas.

Sammanfattningsvis är det maximala avstånd som jeepen kan nå (med en bränslekapacitet för 1 enhet av distans vid varje tidpunkt) i n turer (med n-1 bränsledumpar på mitten och förbrukar totalt n enheter bränsle)

$\mathrm {utforska} (n)={\frac {1}{2 }}H_{n}={\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{6}}+\cdots +{\frac {1}{ 2n}}$ , för att utforska öknen där jeepen måste återvända till basen i slutet av varje resa;
$\mathrm {cross} (n)=H_ {2n-1}-{\frac {1}{2}}H_{n-1}=1+{\frac {1}{3}}+{\frac {1}{5}}+\cdots + {\frac {1}{2n-1}}$ , för att korsa öknen där jeepen måste återvända till basen i slutet av varje resa förutom den sista resan, då jeepen färdas så långt den kan innan den tar slut av bränsle.

Här ${\displaystyle H_{n}=1+{\frac {1}{2}}+{\frac {1}{3}}+\$ är det n:te övertonstalet .

Kontinuerlig mängd bränsle

Antalet tillgängliga bränsleenheter vid basen behöver inte vara ett heltal. I det allmänna fallet är det maximala avstånd som kan uppnås för problemet "utforska öknen" med $n$ enheter bränsle

\mathrm {utforska} (n)=\int _{0}^{n}{\frac {\mathrm { d} f}{2\lceil nf\rceil }}

med den första bränsledumpen placerad vid $\{n\}/(2\lceil n\rceil )$ enheter av avstånd från startbasen, den andra vid $1/(2\lceil n\rceil -2)$ enheter för avstånd från den första bränsledumpen, den tredje vid ${\ displaystyle 1/(2\lceil n\rceil -4)}$ enheter av avstånd från den andra bränsledumpen, och så vidare. Här $\{n\}=n-\lgolv n\rgolv$ bråkdelen av $n$ .

Det maximala avstånd som kan uppnås för "korsa öknen"-problemet med $n$ enheter bränsle är

\mathrm {cross} (n)=\int _{0}^{n}{\frac {\mathrm { d} f}{2\lceil nf\rceil -1}}

med den första bränsledumpen placerad vid $\{n\}/(2\lceil n\rceil -1)$ enheter av avstånd från startbasen, den andra en vid $1/(2\lceil n\rceil -3)$ enheter för avstånd från den första bränsledumpen, den tredje vid $1/(2\lceil n\rceil -5)$ enheter av avstånd från den andra bränsledumpen, och så vidare. Här $\{n\}=n-\lgolv n\rgolv$ bråkdelen av $n$ .

Andra varianter av problemet

I kamel- och bananproblemet antar att handlaren har totalt n=7/3 enheter bananer vid startbasen och marknaden är på m enheter avstånd bort:

Om $m>\mathrm {cross} (n)=1/15+1/3+1$ finns det ingen lösning för det här problemet;
Om $m\leq \mathrm {cross} (n)-\mathrm {cross} (\lfloor n \rfloor )=1/15$ , ingen halvvägs lägerstolpe behövs för transporten, och avståndet m kommer att upprepas $2\lceil n\rceil -1=5$ gånger av kamelen, så den maximala mängden bananer som transporteras till marknaden är $nm\times (2\lceil n\rceil -1) =7/3-5m$ ;
Om ${\displaystyle \mathrm {cross} (n)-\mathrm {cross} (\ lfloor n\rfloor )<m\leq \mathrm {cross} (n)} ,$ $\mathrm {cross} (n)-\mathrm {cross} (\lfloor n\rfloor )<m\leq \mathrm {cross} (n)$ den optimala lösningen för att transportera den maximala mängden bananer kräver några lägerposter mitt på vägen:
1. För m=1/4<(1/3+1/15) krävs endast en lägerpost på mitten på ett avstånd av 1/15 enheter från startbasen, där totalt 2 enheter bananer kommer att samlas. Avståndet från lägerposten till marknaden är (1/4-1/15), vilket kommer att upprepas 3 gånger av kamelen, och den maximala mängden bananer som transporteras till marknaden är 2-(1/4-1/) 15)*3=1,45 enheter;
2. För m=1/2>(1/3+1/15) krävs ytterligare en lägerpost på mitten på ett avstånd av 1/3 enheter från den första lägerposten, där totalt 1 enhet bananer kommer att samlas. Avståndet från den andra lägerposten till marknaden är [1/2-(1/3+1/15)], som endast kommer att resas en gång av kamelen, och den maximala mängden bananer som transporteras till marknaden är 1- [1/2-(1/3+1/15)]*1=0,9 enheter.

Om det krävs att kamelen så småningom återvänder till startbasen, gäller funktionen ${\displaystyle \mathrm {utforska} (n)} (fortfarande under antagande av$ n=7/3 ):

Om $+1/4+1/$ , det finns ingen lösning för detta problem;
Om $m\leq \mathrm {utforska} (n)-\mathrm {utforska} (\lfloor n\rfloor )=1/18$ , ingen halvvägs lägerstolpe behövs för transporten, och sträckan m kommer att upprepas i $2\lceil n\rceil =6$ gånger av kamelen, så den maximala mängden bananer som transporteras till marknaden är $nm\times (2\lceil n\rceil )=7/3 -6m$ ;
Om ${\displaystyle \mathrm {utforska} (n)-\ mathrm {utforska} (\lfloor n\rfloor )<m\leq \mathrm {utforska} (n)} ,$ $\mathrm {explore} (n)-\mathrm {explore} (\lfloor n\rfloor )<m\leq \mathrm {explore} (n)$ den optimala lösningen för att transportera den maximala mängden bananer kräver några lägerposter mitt på vägen:
1. För m=1/4<(1/4+1/18) krävs endast en lägerpost på mitten på ett avstånd av 1/18 enheter från startbasen, där totalt 2 enheter bananer (plus 1/ 18 enheter för kamelens slutliga återkomst) kommer att samlas in. Avståndet från lägerposten till marknaden är (1/4-1/18), vilket kommer att upprepas 4 gånger av kamelen, och den maximala mängden bananer som transporteras till marknaden är 2-(1/4-1/) 18)*4=1,22 enheter;
2. För m=1/2>(1/4+1/18) krävs ytterligare en lägerpost på mitten på ett avstånd av 1/4 enheter från den första lägerposten, där totalt 1 enhet bananer (plus 1/4) enheter för kamelens slutliga återkomst) kommer att tillfalla. Avståndet från den andra lägerposten till marknaden är [1/2-(1/4+1/18)], vilket kommer att upprepas två gånger av kamelen, och den maximala mängden bananer som transporteras till marknaden är 1-[ 1/2-(1/4+1/18)]*2=0,61 enheter.

I problem med resenärer över öknen , antag att n resenärer ger sig av från startbasen med n förrådsenheter. Efter 1/( n +1) enheter av avstånd, skulle de redan ha förbrukat n /( n +1) enheter av leveranser; Vid denna tidpunkt bör en av resenärerna återvända med 1/( n +1) enheter av förnödenheter, vilket lämnar gruppen exakt ( n -1) enheter av förnödenheter så att varje återstående resenär bär exakt en enhet av förnödenheter. Gruppen reser sedan ytterligare 1/( n +1) enheter av avstånd, förbrukar ( n -1)/( n +1) enheter av förråd; Vid denna tidpunkt bör en av de återstående resenärerna återvända med 2/( n +1) enheter av förnödenheter för att säkert komma tillbaka till startbasen, vilket lämnar gruppen exakt ( n -2) enheter av förnödenheter. Gruppen fortsätter att flytta 1/( n +1) enheter av avstånd och minska en resenär, tills det bara finns en resenär kvar som bär exakt en enhet av förnödenheter. Slutligen kan denna resenär resa en enhet av avstånd för att nå den längsta punkten. Totalt är det längsta avståndet n resenärer kan nå

\mathrm {travel} (n)={\frac {n-1}{n+1} }+1=2-{\frac {2}{n+1}}

Genom att likställa detta med m , kan man lösa det minsta antal resenärer som behövs för att resa m enheter av avstånd. Observera att lösningar endast finns för m <2.

Om den sista och sista resenären också behöver återvända till startbasen, skulle han bara resa 1/( n +1) enhet ensam så att han har n /( n +1) leveransenheter att återvända, alltså den längsta sträckan n resenärer kan nå är

\mathrm {travel_{return}} (n)={\frac {n}{n +1}}=1-{\frac {1}{n+1}}

Genom att likställa detta med m kan man lösa det minsta antal resenärer som behövs för att resa m enheter av avstånd. Observera att lösningar endast finns för m <1.

I bilarna över öknen , anta att n bilar ger sig av från startbasen med n enheter bränsle. Efter 1/ n avståndsenheter skulle gruppen redan ha förbrukat exakt en enhet bränsle; Vid det här laget bör de överföra bränsle mellan sig, lämna en tom bil bakom sig och transportera ( n -1) enheter bränsle bland ( n -1) bilar. Efter ytterligare 1/( n -1) avståndsenheter skulle gruppen ha förbrukat ytterligare en enhet bränsle; Återigen bör de överföra bränsle, lämna en tom bil bakom sig och transportera ( n -2) enheter bränsle bland ( n -2) bilar. Gruppen fortsätter att flytta och minska en bil, tills det bara finns en bil kvar som bär exakt en enhet bränsle. Slutligen kan den här bilen resa en enhet av avstånd för att nå den längsta punkten. Totalt är det längsta avståndet n bilar kan nå det n :te övertonstalet :

$H_{n}=1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots + {\frac {1}{n}}$

Genom att likställa detta med m kan man lösa det minsta antal bilar som behövs för att färdas m enheter av avstånd.

Ordna oberoende

Observera att ordningen på jeepturerna inte är fast. Till exempel i "utforska öknen"-versionen av problemet, kunde jeepen göra $n - 1$ tur och retur mellan basen och den första bränsledumpen, vilket lämnar ( $n - 1) / n$ enheter bränsle vid bränsledumpen varje gång och gör sedan en $n:$ e resa enkelriktad till den första bränsledumpen, och kommer därmed dit med totalt $(n - 1) + 1/(2 n)$ tillgängliga bränsleenheter. 1 $/(2 n)$ enheterna sparas för returresan till basen i slutet och de andra $n - 1$ enheterna bränsle används för att flytta bränsle mellan den första och andra bränsledumpen, med $n - 2$ tur och retur och sedan en $(n -1)$ -:e resa enkelriktad till den andra bränsledumpen. Och så vidare.

Praktiska tillämpningar

I Operation Black Buck One tankades den attackerande Vulcan sju gånger på utresan och en gång på hemresan. Grå linjer indikerar reservflygplan för att ersätta skadade.

Problemet kan ha en praktisk tillämpning i krigstidssituationer, särskilt med avseende på bränsleeffektivitet . I samband med bombningen av Japan under andra världskriget av B-29:or säger Robert McNamara i filmen The Fog of War att förståelsen av bränsleeffektivitetsproblemet som orsakades av att behöva transportera bränslet till framåtriktade baser var den främsta anledningen till att strategin att inleda bombräder från Kinas fastland övergavs till förmån för öhoppningsstrategin :

"Vi var tvungna att flyga de här planen från baserna i Kansas till Indien. Sedan var vi tvungna att flyga bränsle över puckeln in i Kina. [...] Vi skulle ta de här B- 29: orna — det fanns inga tankflygplan där. Vi skulle fylla dem med bränsle, flyga från Indien till Chengtu ; lasta av bränslet; flyga tillbaka till Indien; göra tillräckligt med uppdrag för att bygga upp bränsle i Chengtu; flyga till Yawata , Japan ; bomba stålverken ; och åka tillbaka till Indien. Vi hade så lite träning i det här problemet med att maximera [bränsle] effektivitet, vi fann faktiskt att vi fick tillbaka några av B-29:orna istället för att lasta av bränsle, de var tvungna att ta på sig det. För att göra en lång historia kort, det var inte värt och det var LeMay som verkligen kom fram till den slutsatsen och ledde till att cheferna flyttade det hela till Marianerna , som ödelade Japan."

( Atombombningsuppdragen i slutet av andra världskriget flögs med B-29 Superfortresses från Stillahavsön Tinian på norra Marianerna . )

Se även Operation Black Buck för en tillämpning av dessa idéer. I dessa uppdrag, utförda under Falklandskriget , använde Royal Air Force tankning från luft till luft genom att iscensätta tankfartyg för att göra det möjligt för Vulcan- bombplanen baserade på Ascension Island att bomba mål på Falklandsöarna .

Se även