Hyperladdning

Den här artikeln handlar om ett kvantantal hadroner. För liknande antal i elektrosvag teori, se svag hyperladdning .

I partikelfysik är hyperladdningen ( en portmanteau av hyperonisk och ladda ) Y av en partikel ett kvantnummer som bevaras under den starka interaktionen . Konceptet hyperladdning tillhandahåller en enkelladdningsoperator som står för egenskaperna för isospin , elektrisk laddning och smak . Hyperladdningen är användbar för att klassificera hadroner ; den på samma sätt benämnda svaga hyperladdningen har en analog roll i den elektrosvaga interaktionen .

Definition

  Hypercharge är ett av två kvanttal i SU(3)-modellen av hadroner , tillsammans med isospin I ₃ . Enbart isospin räckte för två kvargsmaker — nämligen
u
och
d
— medan för närvarande 6 smaker av kvarkar är kända.

      SU(3) viktdiagram (se nedan) är tvådimensionella, där koordinaterna hänvisar till två kvanttal: I ₃ (även känd som I _z ), som är z- komponenten i isospin, och Y , som är hyperladdningen (den summan av konstigheten S , charmen C , bottenheten B′ , toppheten T′ , och baryonnummer B ). Matematiskt är hyperladdning

$Y=B+S+C+B'+T'~.$

Starka interaktioner bevarar hyperladdning (och svag hyperladdning ), men svaga interaktioner gör det inte .

Relation med elektrisk laddning och isospin

Huvudartikel: Gell-Mann–Nishijima formel

Gell -Mann-Nishijima-formeln relaterar isospin och elektrisk laddning

$Q=I_{3}+{\tfrac {1}{2}}Y,$

där I3 är _den tredje komponenten i isospin och Q är partikelns laddning.

Isospin skapar multipletter av partiklar vars medelladdning är relaterad till hyperladdningen genom:

$Y=2{\bar {Q}}.$

eftersom hyperladdningen är densamma för alla medlemmar i en multiplett, och medelvärdet av I ₃ -värdena är 0.

SU(3)-modell i relation till hyperladdning

SU(2)-modellen har multipletter som kännetecknas av ett kvanttal J , vilket är den totala rörelsemängden . Varje multiplett består av 2 J + 1 subtillstånd med jämnt fördelade värden på _Jz , som bildar ett symmetriskt arrangemang sett i atomspektra och isospin. Detta formaliserar observationen att vissa starka baryonförfall inte observerades, vilket leder till förutsägelse av massan, konstigheten och laddningen av
Ω ⁻
baryonen .

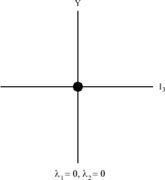
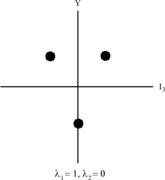
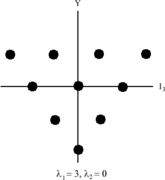
SU(3) har supermultipletter innehållande SU(2)-multipletter. SU(3) behöver nu två siffror för att specificera alla dess deltillstånd som betecknas med λ ₁ och λ ₂ .

( λ ₁ + 1) anger antalet punkter på den översta sidan av hexagonen medan ( λ ₂ + 1) anger antalet punkter på den nedre sidan.

• 

  SU(3) singlet-viktdiagram _, där Y är hyperladdning och I3 är den tredje komponenten i isospin.

• 

  SU(3) triplettviktdiagram

• 

  SU(3) septett-, oktett- och nonetviktdiagram Notera likheten med båda diagrammen till höger. Siffran som används för att beskriva viktdiagrammet beror på om partikeln/partiklarna som upptar mitten av diagrammet har ett, två eller tre distinkta namn.

• 

  Mesoner av spin 0 bildar ett nonet . K: kaon , π: pion , η: eta meson .

• 

  Oktetten av ljusspinn - . 1/2 baryoner som beskrivs i SU(3 ) n: neutron , p: proton , Λ: Lambda baryon , Σ: Sigma baryon , Ξ: Xi baryon .

• 

  SU(3) decuplet viktdiagram Notera likhet med diagrammet till höger.

• 

  3/2 decupleten kombination av tre upp-, ner- eller konstiga kvarkar med en total spin på bildar den så kallade baryon- . De nedre sex är hyperoner. S : konstigt , Q : elektrisk laddning .

Exempel

• Nukleongruppen ( protoner med Q = +1 och neutroner med Q = 0 ) har en medelladdning på + + ( / 2 1 , så de har båda hyperladdning Y = 1 eftersom baryonnummer B = +1 , och S = C = B' = T' = 0 ). Från Gell-Mann–Nishijima-formeln vet vi att protonen har isospin I ₃ = + + 1 / 2 , medan neutronen har I ₃ = − + 1 / 2 .
• Detta fungerar även för kvarkar : För uppkvarken , med en laddning på + + 2 / 3 , och en I ₃ på + + 1 / 2 , härleder vi en hyperladdning på 1 / 3 , på grund av dess baryonnummer (eftersom tre kvarkar gör en baryon, varje kvark har ett baryonnummer på + + 1 / 3 ).
• För en märklig kvark, med elektrisk laddning − + 1 / 3 , ett baryontal på + + 1 / 3 , och märklighet −1, får vi en hyperladdning Y = − + 2 / 3 , så vi härleder att I ₃ = 0 . Det betyder att en märklig kvark gör en egen isospin-singel (detsamma händer med charm , botten- och toppkvarkar ), medan upp och ner utgör en isospin-dubbel.

Praktisk inkurans

Hypercharge var ett koncept som utvecklades på 1960-talet, för att organisera grupper av partiklar i " partikelzoo " och för att utveckla ad hoc bevarandelagar baserat på deras observerade transformationer. Med tillkomsten av kvarkmodellen är det nu uppenbart att stark hyperladdning, Y , är följande kombination av siffrorna upp ( n _u ), ner ( n _d ), konstigt ( n _s ), charm ( n _c ), topp ( n _t ) och botten ( n _b ):

$Y={\tfrac {1}{3}}n_{\textrm {u}}+{\tfrac {1}{3}}n_{\textrm {d}}-{\tfrac {2}{ 3}}n_{\textrm {s}}+{\tfrac {4}{3}}n_{\textrm {c}}-{\tfrac {2}{3}}n_{\textrm {b}}+ {\tfrac {4}{3}}n_{\textrm {t}}~.$

I moderna beskrivningar av hadroninteraktion har det blivit mer uppenbart att rita Feynman-diagram som spårar genom de individuella kvarkarna (som är bevarade) som utgör de interagerande baryonerna och mesonerna , snarare än att bry sig om att räkna starka hyperladdningskvantumtal. Svag hyperladdning är dock fortfarande en viktig del av att förstå den elektrosvaga interaktionen .

•   Semat, Henry; Albright, John R. (1984). Introduktion till atom- och kärnfysik . Chapman och Hall. ISBN 978-0-412-15670-0 .