Hyperbolastiska funktioner

Grafik som beskriver Hyperbolastic Type I-funktionen med varierande parametervärden.

Grafik som beskriver Hyperbolastic Type I-funktionen med varierande parametervärden.

Grafik som beskriver Hyperbolastic Type II-funktionen med varierande parametervärden.

Grafik som beskriver Hyperbolastic Type II-funktionen med varierande parametervärden.

Grafik som beskriver Hyperbolastic Type III-funktionen med varierande parametervärden.

Grafik som beskriver den hyperbolastiska kumulativa distributionsfunktionen av typ III med varierande parametervärden.

Grafik som beskriver den hyperbolastiska sannolikhetstäthetsfunktionen av typ III med varierande parametervärden.

Hyperbolastiska funktioner , även kända som hyperbolastiska tillväxtmodeller , är matematiska funktioner som används i medicinsk statistisk modellering . Dessa modeller utvecklades ursprungligen för att fånga tillväxtdynamiken hos flercelliga tumörsfärer och introducerades 2005 av Mohammad Tabatabai, David Williams och Zoran Bursac. Precisionen hos hyperbolastiska funktioner vid modellering av verkliga problem beror något på deras flexibilitet i deras böjningspunkt. Dessa funktioner kan användas i en mängd olika modelleringsproblem såsom tumörtillväxt, stamcellsproliferation , farmakinetik, cancertillväxt, sigmoidaktiveringsfunktion i neurala nätverk och epidemiologisk sjukdomsprogression eller regression.

De hyperbolastiska funktionerna kan modellera både tillväxt- och avklingningskurvor tills den når bärkraft . På grund av sin flexibilitet har dessa modeller olika tillämpningar inom det medicinska området, med förmågan att fånga sjukdomsprogression med en mellanliggande behandling. Som figurerna indikerar hyperbolastiska funktioner passa en sigmoidal kurva som indikerar att den lägsta hastigheten inträffar i de tidiga och sena stadierna. Förutom de uppvisande sigmoidala formerna kan den också rymma bifasiska situationer där medicinska ingrepp bromsar eller vänder sjukdomsprogression; men när effekten av behandlingen försvinner, kommer sjukdomen att börja den andra fasen av sin progression tills den når sin horisontella asymptot.

En av de viktigaste egenskaperna som dessa funktioner har är att de inte bara kan passa sigmoidala former, utan kan också modellera bifasiska tillväxtmönster som andra klassiska sigmoidala kurvor inte kan modellera tillräckligt. Denna särskiljande egenskap har fördelaktiga tillämpningar inom olika områden, inklusive medicin, biologi, ekonomi, ingenjörsvetenskap, agronomi och datorstödd systemteori.

Funktion H1

Ekvationen för hyperbolastisk hastighet av typ I, betecknad H1, ges av

$${\frac {dP(x)}{dx}}={\ frac {P(x)}{M}}\left(MP\left(x\right)\right)\left(\delta +{\frac {\theta }{\sqrt {1+x^{2}} }}\höger),$$

där $x$ är valfritt reellt tal och $P\left(x\right)$ är populationsstorleken vid $x$ . Parametern $M$ representerar bärförmåga, och parametrarna $\delta$ och $\theta$ representerar tillsammans tillväxthastighet. Parametern $\theta$ anger avståndet från en symmetrisk sigmoidal kurva. Att lösa den hyperbolastiska hastighetsekvationen av typ I för $P\left(x\right)$ ger

$$P(x)={\frac {M}{1+\alpha e^{-\delta x-\theta \operatörsnamn {arsinh} (x)}}},$$

där $\operatornamn {arsinh}$ är den inversa hyperboliska sinusfunktionen . Om man vill använda initialvillkoret $P\left(x_{0}\right)=P_{0}$ , då kan $\alpha$ uttryckas som

$\alpha ={\frac {M-P_{0}}{P_{0}}}e^{\delta x_{0}+ \theta \operatörsnamn {arsinh} (x_{0})}$ .

Om $x_{0}=0$ minskar $\alpha$ till

$\alpha ={\frac {M-P_{0}}{P_{0}}}$ .

Den hyperbolastiska funktionen av typ I generaliserar den logistiska funktionen . Om parametrarna $\theta =0$ , så skulle det bli en logistisk funktion. Denna funktion $P(x)$ är en hyperbolastisk funktion av typ I . Standard hyperbolastisk funktion av typ I är

$P(x)={\frac {1}{1+e^{-x-\theta \operatörsnamn {arsinh} (x )}}}$ .

Funktion H2

Hyperbolastisk hastighetsekvation av typ II, betecknad med H2, definieras som

${\frac {dP(x)}{ dx}}={\frac {\alpha \delta \gamma P^{2}(x)x^{\gamma -1}}{M}}\tanh \left({\frac {MP(x)}{ \alpha P(x)}}\höger),$

där $\tanh$ är den hyperboliska tangentfunktionen , $M$ är bärförmågan, och både $\delta$ och $\gamma >0$ bestämmer tillsammans tillväxthastigheten . Dessutom representerar parametern $\gamma$ acceleration i tidsförloppet. Att lösa hyperbolastic rate-funktionen av typ II för $P\left(x\right)$ ger

$P(x)={\frac {M}{1+\alpha \operatörsnamn {arsinh} \left(e^{-\ delta x^{\gamma }}\right)}}$ .

Om man vill använda initialvillkoret $P(x_{0})=P_{0},$ så kan ${\displaystyle \alpha } uttryckas som$

$\alpha ={\frac {M-P_{0}}{P_{0}\operatörsnamn {arsinh} \left(e^{-\ delta x_{0}^{\gamma }}\right)}}$ .

Om $x_{0}=0$ minskar $\alpha$ till

$\alpha ={\frac {M-P_{0}}{P_{0}\operatörsnamn {arsinh} (1)}}$ .

Standard hyperbolastisk funktion av typ II definieras som

$P(x)={\frac {1}{1+\operatörsnamn {arsinh} \left(e^{-x}\right)} }$ .

Funktion H3

Hyperbolastisk hastighetsekvation av typ III betecknas med H3 och har formen

${\frac {dP(t)}{dt}}=\ left(MP\left(t\right)\right)\left(\delta \gamma t^{\gamma -1}+{\frac {\theta }{\sqrt {1+\theta ^{2}t^ {2}}}}\right)$ ,

där $t$ > 0. Parametern $M$ representerar bärförmågan, och parametrarna $\delta ,$$\gamma ,$ och $\ theta$ bestämmer gemensamt tillväxttakten. Parametern $\gamma ,$ representerar accelerationen av tidsskalan, medan storleken på $\theta$ representerar avståndet från en symmetrisk sigmoidal kurva. Lösningen på differentialekvationen för typ III är

$P(t)=M-\alpha e^{-\delta t^{\gamma }-\operatörsnamn {arsinh} (\theta t)}$ ,

med initialvillkoret $P\left(t_{0}\right)=P_{0}$ kan vi uttrycka $\alpha$ som

$\alpha =\left(M-P_{0}\right)e^{\delta t_{0}^{\gamma } +\operatörsnamn {arsinh} (\theta t_{0})}$ .

Den hyperbolastiska fördelningen av typ III är en treparameterfamilj av kontinuerliga sannolikhetsfördelningar med skalparametrar $\delta$ > 0, och $\theta$ ≥ 0 och parametern $\gamma$ som form parameter . När parametern $\theta$ = 0 reduceras den hyperbolastiska fördelningen av typ III till weibullfördelningen . Den hyperbolastiska kumulativa fördelningsfunktionen för typ III ges av

$F(x;\delta ,\gamma ,\theta )={\ start{cases}1-e^{-\delta x^{\gamma}-\operatörsnamn {arsinh} (\theta x)}&x\geq 0,\\0&x<0\end{cases}}$ ,

och dess motsvarande sannolikhetstäthetsfunktion är

$f( x;\delta ,\gamma ,\theta )={\begin{cases}e^{-\delta x^{\gamma}-\operatörsnamn {arsinh} (\theta x)}\left(\delta \gamma x ^{\gamma -1}+{\frac {\theta }{\sqrt {1+\theta ^{2}x^{2}}}}\right)&x\geq 0,\\0&x<0\end {fall}}$ .

Riskfunktionen $h$ (eller felfrekvensen) ges av

$h\left(x;\delta ,\gamma ,\theta \right)=\delta \gamma x^{\gamma -1}+{\frac {\theta }{\sqrt {1+x^{ 2}\theta ^{2}}}}.$

Överlevnadsfunktionen $\displaystyle S}$ { ges av

$S(x;\delta ,\gamma ,\theta )=e^{-\delta x^{\gamma }-\operatörsnamn {arsinh} (\theta x)}.$

Standardfunktionen för hyperbolastisk kumulativ distribution av typ III definieras som

$F\left(x\right)=1-e^{-x-\operatörsnamn {arsinh} (x)}$ ,

och dess motsvarande sannolikhetstäthetsfunktion är

$f(x)=e^{-x-\operatörsnamn {arsinh} (x)}\left(1) +{\frac {1}{\sqrt {1+x^{2}}}}\right)$ .

Egenskaper

Om man vill beräkna punkten $x$ där populationen når en procentandel av sin bärförmåga $M$ , då kan man lösa ekvationen

$P(x)=kM$

för $x$ , där $0<k<1$ . Till exempel kan halvpunkten hittas genom att sätta $k={\frac {1}{2}}$ .

Ansökningar

3D hyperbolastisk graf över växtplanktonbiomassa som en funktion av näringsämneskoncentration och tid

Enligt stamcellsforskare vid McGowan Institute for Regenerative Medicine vid University of Pittsburgh, "är en nyare modell [kallad hyperbolastisk typ III eller] H3 en differentialekvation som också beskriver celltillväxten. Denna modell möjliggör mycket mer variation och har har visat sig bättre förutsäga tillväxt."

De hyperbolastiska tillväxtmodellerna H1, H2 och H3 har använts för att analysera tillväxten av solid Ehrlich-karcinom med användning av en mängd olika behandlingar.

Inom djurvetenskapen har hyperbolastiska funktioner använts för att modellera broilerkycklingstillväxt. Den hyperbolastiska modellen av typ III användes för att bestämma storleken på det återhämtande såret.

Inom området för sårläkning representerar de hyperbolastiska modellerna exakt läkningens tidsförlopp. Sådana funktioner har använts för att undersöka variationer i läkningshastigheten mellan olika typer av sår och i olika stadier i läkningsprocessen med hänsyn till områdena spårämnen, tillväxtfaktorer, diabetiska sår och näring.

En annan tillämpning av hyperbolastiska funktioner är inom området för den stokastiska diffusionsprocessen , vars medelfunktion är en hyperbolastisk kurva. Processens huvudsakliga egenskaper studeras och den maximala sannolikhetsuppskattningen för processens parametrar beaktas. För detta ändamål tillämpas den eldfluga metaheuristiska optimeringsalgoritmen efter att ha begränsat det parametriska utrymmet genom en stegvis procedur. Några exempel baserade på simulerade provvägar och verkliga data illustrerar denna utveckling. En provbana för en diffusionsprocess modellerar banan för en partikel som är inbäddad i en strömmande vätska och utsatts för slumpmässiga förskjutningar på grund av kollisioner med andra partiklar, vilket kallas Brownsk rörelse . Den hyperbolastiska funktionen av typ III användes för att modellera proliferationen av både vuxna mesenkymala och embryonala stamceller ; och den hyperbolastiska blandade modellen av typ II har använts vid modellering av livmoderhalscancerdata . Hyperbolastiska kurvor kan vara ett viktigt verktyg för att analysera celltillväxt, anpassning av biologiska kurvor, tillväxten av växtplankton och momentan mognadshastighet.

Inom skogsekologi och skogsskötsel har hyperbolastiska modeller tillämpats för att modellera förhållandet mellan DBH och höjd.

Den multivariabla hyperbolastiska modellen typ III har använts för att analysera tillväxtdynamiken hos växtplankton med hänsyn till koncentrationen av näringsämnen.

Hyperbolastiska regressioner

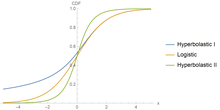
Kumulativ distributionsfunktion för Hyperbolastic Typ I, Logistic och Hyperbolastic Typ II

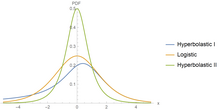
PDF av H1, Logistic och H2

Hyperbolastiska regressioner är statistiska modeller som använder standard hyperbolastiska funktioner för att modellera en dikotom eller multinomial utfallsvariabel. Syftet med hyperbolastisk regression är att förutsäga ett utfall med hjälp av en uppsättning förklarande (oberoende) variabler. Dessa typer av regressioner används rutinmässigt inom många områden, inklusive medicinsk, folkhälsa, tandvård, biomedicin samt social-, beteende- och ingenjörsvetenskap. Till exempel har binär regressionsanalys använts för att förutsäga endoskopiska lesioner vid järnbristanemi . Dessutom användes binär regression för att skilja mellan malign och benign adnexal massa före operation.

Den binära hyperbolastiska regressionen av typ I

Låt $Y$ vara en binär utfallsvariabel som kan anta ett av två ömsesidigt uteslutande värden, framgång eller misslyckande. Om vi ​​kodar framgång som $Y=1$ och misslyckande som $Y=0$ , då för parametern $\theta \geq -1$ , den hyperbolastiska framgångssannolikheten av typ I med ett urval av storleken $n$ som funktion av parametern $\theta$ och parametervektorn ${\boldsymbol {\ beta }}=(\beta _{0},\beta _{1},\ldots ,\beta _{p})$ givet en $p$ -dimensionell vektor av förklarande variabler definieras som $\mathbf {x} _{i}=(x_{i1},\ x_{i2},\ldots ,\ x_{ip}) ^{T}$ , där $i=1,2,\ldots ,n$ , ges av

$\pi (\mathbf {x} _{i};{\boldsymbol {\beta }})=P(y_{i}=1|\mathbf {x} _{ i};{\boldsymbol {\beta }})={\frac {1}{1+e^{-(\beta _{0}+\summa _{s=1}^{p}{\beta _ {s}x_{är}})-\theta \operatörsnamn {arsinh} (\beta _{0}+\summa _{s=1}^{p}{\beta _{s}x_{is}}) }}}$ .

Oddsen för framgång är förhållandet mellan sannolikheten för framgång och sannolikheten för misslyckande. För binär hyperbolastisk regression av typ I betecknas oddsen för framgång med $Odds_{H1}$ och uttrycks med ekvationen

$Odds_{H1}=e^{\ beta _{0}+\summa _{s=1}^{p}{\beta _{s}x_{is}}+\theta \operatörsnamn {arsinh} (\beta _{0}+\summa _{ s=1}^{p}{\beta _{s}x_{är}})}$ .

Logaritmen för $Odds_{H1}$ kallas logit för binär hyperbolastisk regression av typ I. Logittransformationen betecknas med $L_{H1}$ och kan skrivas som

$L_{H1}=\beta _{0}+\ summa _{s=1}^{p}{\beta _{s}x_{is}}+\theta \operatörsnamn {arsinh} [\beta _{0}+\summa _{s=1}^{p }{\beta _{s}x_{är}}]$ .

Shannon-information för binär hyperbolastisk typ I (H1)

Shannon -informationen för slumpvariabeln $Y$ definieras som

$I(y)=-{log}_{b}P(y)$

där basen för logaritmen $b>0$ och $b\neq 1$ . För binärt utfall $b$ lika med $2$ .

ges informationen ${\displaystyle I(y)} av$

$I(y)={\begin{cases}-log_{b}{\frac {1}{1+e^{-Z-\theta \operatorname {arsinh} (Z )}}}&y=1,\\-log_{b}{\frac {e^{-Z-\theta \operatörsnamn {arsinh} (Z)}}{1+e^{-Z-\theta \operatörsnamn {arsinh} (Z)}}}&y=0\end{cases}}$ ,

där $Z=\beta _{0}+\summa _{s=1}^{p}\beta _{s}x_{s}$ , och $x_{s}$ är $s^{th}$ indata. För ett slumpmässigt urval av binära utfall av storleken $n$ kan den genomsnittliga empiriska informationen för hyperbolastisk H1 uppskattas med

${\overline {I(y)}}={\begin{cases}-{ \frac {1}{n}}\sum _{i=1}^{n}{log_{b}{\frac {1}{1+e^{-Z_{i}-\theta \operatörsnamn {arsinh } (Z_{i})}}}}&y=1,\\-{\frac {1}{n}}\summa _{i=1}^{n}{log_{b}{\frac {e ^{-Z_{i}-\theta \operatorname {arsinh} (Z_{i})}}{1+e^{-Z_{i}-\theta \operatorname {arsinh} (Z_{i})}} }}&y=0\end{cases}}$ ,

där $Z_{i}=\beta _{0}+\summa _{s=1}^{p}\beta _{s}x_ {is}$ och $x_{is}$ är $s^{th}$ indata för ${\displaystyle i^{th}}-$ observationen.

Information Entropi för hyperbolastisk H1

Informationsentropi mäter förlusten av information i ett överfört meddelande eller en signal. I maskininlärningsapplikationer är det antalet bitar som krävs för att sända en slumpmässigt vald händelse från en sannolikhetsfördelning. För en diskret slumpvariabel $Y$ definieras informationsentropin ${\displaystyle H} som$

$H=-\summa _{y\in Y}{P(y)\ {log}_{b}P(y )}$

där $P(y)$ är sannolikhetsmassfunktionen för slumpvariabeln $Y$ .

Informationsentropin är den matematiska förväntan av $I(y)$ med avseende på sannolikhetsmassfunktionen $P(y)$ . Informationsentropin har många tillämpningar inom maskininlärning och artificiell intelligens såsom klassificeringsmodellering och beslutsträd. För den hyperbolastiska H1 är entropin $H$ lika med

${\begin{aligned}H& =-\summa _{y\in \{0,1\}}{P(Y=y;\mathbf {x} ,{\boldsymbol {\beta }})log_{b}(P(Y=y; \mathbf {x} ,{\boldsymbol {\beta }}))}\\&=-[\pi (\mathbf {x} ;{\boldsymbol {\beta }})\ log_{b}(\pi ( \mathbf {x} ;{\boldsymbol {\beta }})+(1-\pi (\mathbf {x} ;{\boldsymbol {\beta }}))log_{b}(1-\pi (\mathbf {x} ;{\boldsymbol {\beta }}))]\\&={log}_{b}(1+e^{-Z-\theta \operatörsnamn {arsinh} (Z)})-{\ frac {e^{-Z-\theta \operatörsnamn {arsinh} (Z)}{log}_{b}(e^{-Z-\theta \operatörsnamn {arsinh} (Z)})}{1+e ^{-Z-\theta \operatörsnamn {arsinh} (Z)}}}\end{aligned}}$

Den uppskattade medelentropin för hyperbolastisk H1 betecknas med ${\bar {H}}$ och ges av

${\bar {H}}={\frac {1}{n}}\ summa _{i=1}^{n}{[log_{b}(1+e^{{-Z}_{i}-\theta \operatörsnamn {arsinh} (Z_{i})})-}{ \frac {e^{{-Z}_{i}-\theta \operatörsnamn {arsinh} (Z_{i})}\ {log}_{b}(e^{{-Z}_{i}- \theta \operatörsnamn {arsinh} ((Z_{i})})}{1+e^{{-Z}_{i}-\theta \operatörsnamn {arsinh} (Z_{i})}}}]$

Binär korsentropi för hyperbolastisk H1

Den binära korsentropin jämför den observerade $y\in \{0,1\}$ med de förutsagda sannolikheterna. Den genomsnittliga binära korsentropin för hyperbolastisk H1 betecknas med ${\overline {C}}$ och är lika med

${\begin{aligned}{\overline {C}}&=-{\frac {1}{n}}\summa _{i=1}^{n}{{[y }_{i}log_{b}(\pi (x_{i};{\boldsymbol {\beta }}))+}{(1-y}_{i})log_{b}(1-\pi (x_{i};{\boldsymbol {\beta }}))]\\&={\frac {1}{n}}\summa _{i=1}^{n}{[log_{b}( 1+e^{{-Z}_{i}-\theta \operatörsnamn {arsinh} (Z_{i})})-}{(1-y}_{i})log_{b}(e^{ {-Z}_{i}-\theta \operatorname {arsinh} (Z_{i})})]\end{aligned}}$

Kullback-Leibler-divergens för hyperbolastisk H1

Kullback-Leibler divergens är ett olikhetsmått som uppskattar antalet bitar som krävs för att representera ett meddelande när hyperbolastisk sannolikhetsfördelning H1 används och är lika med

${KLD}={\frac {e^{-Z-\theta \operatörsnamn {arsinh} (Z)}{log}_{b}( e^{-Z-\theta \operatörsnamn {arsinh} (Z)})}{1+e^{-Z-\theta \operatörsnamn {arsinh} (Z)}}}-(1-y)log_{b }(e^{-Z-\theta \operatörsnamn {arsinh} (Z)})$

och medelvärdet för Kullback-Leibler Divergence ${\overline {KLD}}$ är

${\overline {KLD}}={\frac {1} {n}}\summa _{i=1}^{n}{[{\frac {e^{{-Z}_{i}-\theta \operatörsnamn {arsinh} (Z_{i})}\ { log}_{b}(e^{{-Z}_{i}-\theta \operatörsnamn {arsinh} (Z_{i})})}{1+e^{{-Z}_{i}- \theta \operatorname {arsinh} (Z_{i})}}}-}{(1-y}_{i})log_{b}(e^{{-Z}_{i}-\theta \operatorname {arsinh} (Z_{i})})]$

Den binära hyperbolastiska regressionen av typ II

Den hyperbolastiska regressionen av typ II är en alternativ metod för analys av binära data med robusta egenskaper. För den binära utfallsvariabeln $Y$ är den hyperbolastiska framgångssannolikheten för typ II en funktion av en $p$ -dimensionell vektor av förklarande variabler $\mathbf {x} _{i}$ ges av

$\pi ( \mathbf {x} _{i};{\boldsymbol {\beta }})=P(y_{i}=1|\mathbf {x} _{i};{\boldsymbol {\beta }})={ \frac {1}{1+\operatörsnamn {arsinh} [e^{-(\beta _{0}+\summa _{s=1}^{p}{\beta _{s}x_{is}} )}]}}$ ,

För den binära hyperbolastiska regressionen av typ II betecknas oddsen för framgång med $Odds_{H2}$ och definieras som

$Odds_{H2}={\frac {1}{\operatörsnamn {arsinh} [e^{-(\beta _{0}+\summa _{s=1}^{p}{\beta _{ s}x_{är}})}]}}.$

Logit-transformationen $L_{H2}$ ges av

$L_{H2}=-\log {(\operatörsnamn {arsinh} [e^ {-(\beta _{0}+\summa _{s=1}^{p}{\beta _{s}x_{är}})}])}$

Shannon-information för binär hyperbolastisk typ II (H2)

ges Shannon-informationen ${\displaystyle I(y)} av$

$I(y)={\begin{cases}-log_{b}{\frac {1}{1+arsinh(e^{-Z})}}&y= 1\\-log_{b}{\frac {arsinh(e^{-Z})}{1+arsinh(e^{-Z})}}&y=0\end{cases}}$

där $Z=\beta _{0}+\summa _{s=1}^{p}\beta _{s}x_{s}$ , och $x_{s}$ är $s^{th}$ indata. För ett slumpmässigt urval av binära utfall av storleken $n$ uppskattas den genomsnittliga empiriska informationen för hyperbolastisk H2 med

${\overline {I(y)}}={\begin{cases}-{\ frac {1}{n}}\sum _{i=1}^{n}log_{b}{\frac {1}{1+arsinh(e^{-Z_{i}})}}&y=1 \\-{\frac {1}{n}}\sum _{i=1}^{n}log_{b}{\frac {arsinh(e^{-Z_{i}})}{1+arsinh (e^{-Z_{i}})}}&y=0\end{cases}}$

där $Z_{i}=\beta _{0}+\summa _{s=1}^{p}\beta _{s}x_ {is}$ och $x_{is}$ är $s^{th}$ indata för ${\displaystyle i^{th}}-$ observationen.

Information Entropi för hyperbolastisk H2

För den hyperbolastiska H2 är informationsentropin $H$ lika med

${\ start{aligned}H&=-\summa _{y\in \{0,1\}}{P(Y=y;\mathbf {x} ,{\boldsymbol {\beta }})log_{b}(P (Y=y;\mathbf {x} ,{\boldsymbol {\beta }})}\\&=-[\pi (\mathbf {x} ;{\boldsymbol {\beta }})\ log_{b }(\pi (\mathbf {x} ;{\boldsymbol {\beta }}))+(1-\pi (\mathbf {x} ;{\boldsymbol {\beta }}))log_{b}(1 -\pi (\mathbf {x} ;{\boldsymbol {\beta }}))]\\&=log_{b}(1+arsinh(e^{-Z}))-{\frac {arsinh(e ^{-Z})log_{b}(arsinh(e^{-Z}))}{1+arsinh(e^{-Z})}}\end{aligned}}$

och den uppskattade medelentropin ${\bar {H}}$ för hyperbolastisk H2 är

${\bar {H}}={\frac {1}{n}}\summa _{i=1}^{n}{[log_{b}(1+{arsinh(e}^{{-Z}_{i}}))-}{\frac {{arsinh(e}^{ {-Z}_{i}})\ {log}_{b}{(arsinh(e}^{{-Z}_{i}}))}{1+{arsinh(e}^{{- Z}_{i}})}}]$

Binär korsentropi för hyperbolastisk H2

Den genomsnittliga binära korsentropin ${\overline {C}}$ för hyperbolastisk H2 är

${\begin{aligned}{\overline {C}}&=-{\frac {1}{n}}\summa _{i=1}^{n}{{[y }_{i}log_{b}(\pi (x_{i};\beta ))+}{(1-y}_{i})log_{b}(1-\pi (x_{i}); \beta ))]\\&={\frac {1}{n}}\sum _{i=1}^{n}{[log_{b}(1+{arsinh(e}^{{-Z }_{i}}))-}{(1-y}_{i})log_{b}({arsinh(e}^{{-Z}_{i}}))]\end{aligned} }$

Kullback-Leibler-divergens för hyperbolastisk H2

För hyperbolastisk H2 är Kullback-Leibler-divergensen lika med

$KLD={\frac {{arsinh(e}^{-Z}){log}_{b}{(arsinh(e }^{-Z}))}{1+{arsinh(e}^{-Z})}}-(1-y)log_{b}({arsinh(e}^{-Z}))$

och medelvärdet för Kullback-Leibler Divergence ${\overline {KLD}}$ är

${\overline {KLD}}={\frac {1} {n}}\summa _{i=1}^{n}{[{\frac {{arsinh(e}^{{-Z}_{i}})\ {log}_{b}{(arsinh (e}^{{-Z}_{i}}))}{1+{arsinh(e}^{{-Z}_{i}})}}-}{(1-y}_{i })log_{b}({arsinh(e}^{{-Z}_{i}}))]$

Parameteruppskattning för binär hyperbolastisk regression av typ I och II

Uppskattningen av parametervektorn ${\boldsymbol {\beta }}$ kan erhållas genom att maximera log-likelihood-funktionen

${\ hat {\beta }}={\underset {\boldsymbol {\beta }}{\operatörsnamn {argmax} }}{\summa _{i=1}^{n}[y_{i}ln(\pi (\ mathbf {x} _{i};{\boldsymbol {\beta }}))+(1-y_{i})ln(1-\pi (\mathbf {x} _{i};{\boldsymbol {\ beta }}))]}$

där $\pi (\mathbf {x} _{i};{\boldsymbol {\beta }})$ definieras enligt en av de två typerna av hyberbolastiska funktioner som används.

Multinomial hyperbolastisk regression av typ I och II

Generaliseringen av den binära hyperbolastiska regressionen till multinomial hyperbolastisk regression har en svarsvariabel $y_{i}$ för individuella $i$ med $k$ -kategorier (dvs ${\displaystyle y_{i}\in \{1,2,\ldots ,k\}} )$ . När $k=2$ reduceras denna modell till en binär hyperbolastisk regression. För varje $i=1,2,\ldots ,n$ , bildar vi $k-1$ indikatorvariabler $y_{ij}$ var

$y_{ij}={\begin{cases}1&{\text{if }}y_{i}=j,\\0&{ \text{if }}y_{i}\neq j\end{cases}}$ ,

vilket betyder att $y_{ij}=1$ när ${\displaystyle i^{th}}-$ svaret är i kategori $j$ och $0$ annars.

Definiera parametervektor ${\boldsymbol {\beta }}_{j}=(\beta _{j0},\beta _{j1} ,\ldots ,\beta _{jp})$ i ett $p+1$ -dimensionellt euklidiskt utrymme och ${\boldsymbol { \beta }}=({\boldsymbol {\beta }}_{1},\ldots ,{\boldsymbol {\beta }}_{k-1})^{T}$ .

Använder kategori 1 som referens och $\pi _{1}(\mathbf {x} _{i};{\boldsymbol {\beta }})$ som motsvarande sannolikhetsfunktion , definieras den multinomiala hyperbolastiska regressionen av typ I-sannolikheter som

$\pi _{1}(\mathbf {x} _{i};{\boldsymbol {\beta }})=P(y_{i}=1|\mathbf {x} _{i};{\boldsymbol {\beta }})={\frac {1}{1+\sum _{s=1}^{k-1}e^{-\eta _{s}(\ mathbf {x} _{i};{\boldsymbol {\beta }})-\theta \operatörsnamn {arsinh} [\eta _{s}(\mathbf {x} _{i};{\boldsymbol {\beta }})]}}}$

och för $j=2,\ldots ,k-1$ ,

$\pi _{j}(\mathbf {x} _{i};{ \boldsymbol {\beta }})=P(y_{i}=j|\mathbf {x} _{i};{\boldsymbol {\beta }})={\frac {e^{-\eta _{ j}(\mathbf {x} _{i};{\boldsymbol {\beta }})-\theta \operatörsnamn {arsinh} [\eta _{j}(\mathbf {x} _{i};{\ fetstil {\beta }})]}}{1+\sum _{s=1}^{k-1}e^{-\eta _{s}(\mathbf {x} _{i};{\ fetsymbol {\beta }})-\theta \operatörsnamn {arsinh} [\eta _{s}(\mathbf {x} _{i};{\boldsymbol {\beta }})]}}}$

$\pi _{k}(\mathbf {x} _{i};{\boldsymbol {\beta } })=1-\summa _{j=1}^{k-1}\pi _{j}(\mathbf {x} _{i};{\boldsymbol {\beta }})$

På liknande sätt har vi för den multinomiala hyperbolastiska regressionen av typ II

$\pi _{1}(\mathbf {x} _{i};{\boldsymbol {\beta }})=P(y_{i}=1|\mathbf {x} _{i};{ \boldsymbol {\beta }})={\frac {1}{1+\sum _{s=1}^{k-1}arsinh[e^{-\eta _{s}(\mathbf {x} _{i};{\boldsymbol {\beta }})}]}}$

och för $j=2,\ldots ,k-1$ ,

$\pi _{j}(\mathbf {x} _{i};{\boldsymbol {\beta }})=P(y_ {i}=j|\mathbf {x} _{i};{\boldsymbol {\beta }})={\frac {arsinh[e^{-\eta _{j}(\mathbf {x} _{ i};{\boldsymbol {\beta }})}]}{1+\sum _{s=1}^{k-1}arsinh[e^{-\eta _{s}(\mathbf {x} _{i};{\boldsymbol {\beta }})}]}}$

$\pi _{k}(\mathbf {x} _{i};{\boldsymbol {\beta }})=1-\summa _{j=1}^{k-1}\pi _{j}(\mathbf {x} _{i};{\boldsymbol {\beta }})$

Valet av ${\displaystyle \pi _{i}(\mathbf {x_{i}} ;{\boldsymbol {\beta }})} beror$ på valet av hyperbolastisk H1 eller H2 .

Shannon Information för multiklass hyperbolastisk H1 eller H2

För multiklassen $(j=1,2,\dots ,k)$ är Shannon-informationen $I_{j}$

$I_{j}=-log_{b}(\pi _{j}(\mathbf {x} ;{\boldsymbol {\beta }}))$ .

För ett slumpmässigt urval av storleken $n$ kan den empiriska multiklassinformationen uppskattas med

${\overline {I_{j}}}=-{\frac {1}{n} }\summa _{i=1}^{n}{log_{b}(\pi _{j}(\mathbf {x_{i}} ;{\boldsymbol {\beta }}))}$ .

Flerklassentropi i informationsteori

För en diskret slumpvariabel $Y$ definieras multiklassinformationsentropin som

$H=-\summa _{y\in Y}{P(y)\ {log}_{b}P(y )}$

där $P(y)$ är sannolikhetsmassfunktionen för multiklass-slumpvariabeln $Y$ .

För hyperbolastiska H1 eller H2 är multiklassentropin $H$ lika med

$H=-\summa _{j=1}^{k}{[ \pi _{j}(\mathbf {x} ;{\boldsymbol {\beta }})log_{b}(\pi _{j}(\mathbf {x} ;{\boldsymbol {\beta }})) ]}$

Den uppskattade genomsnittliga multiklassentropin ${\overline {H}}$ är lika med

${\overline {H}} =-{\frac {1}{n}}\summa _{i=1}^{n}{\summa _{j=1}^{k}{[\pi _{j}(\mathbf {x_ {i}} ;{\boldsymbol {\beta }})log_{b}(\pi _{j}(\mathbf {x_{i}} ;{\boldsymbol {\beta }}))]}}$

Multiclass Cross-entropy för hyperbolastisk H1 eller H2

Multiclass cross-entropy jämför den observerade multiklassutdatan med de förutsagda sannolikheterna. För ett slumpmässigt urval av flerklassresultat av storleken $n$ kan den genomsnittliga multiklass-korsentropin ${\overline {C}}$ för hyperbolastisk H1 eller H2 uppskattas med

${\overline {C}}=-{\frac {1}{n}}\summa _{i=1}^{n}{\summa _{j=1}^{k}{[y_{ij}log_{b}(\pi _{j}( \mathbf {x_{i}} ;{\boldsymbol {\beta }}))]}}$

Kullback-Leibler Divergence för multiklass hyperbolastisk H1 eller H2

Den genomsnittliga Kullback-Leibler-divergensen ${\overline {KLD}}$ för multiklasshyperbolastisk H1 eller H2 är lika med

${\ displaystyle {\overline {KLD}}=-{\frac {1}{n}}\sum _{i=1}^{n}{\summa _{j=1}^{k}{[(y_{ ij}-\pi _{j}(\mathbf {x_{i}} ;{\boldsymbol {\beta }}))log_{b}(\pi _{j}(\mathbf {x_{i}} ; {\boldsymbol {\beta }}))]}}}$

Loggoddsen för medlemskap i kategori $j$ kontra referenskategori 1, betecknad med $\eta _{j}(\mathbf {x} _{i}; {\boldsymbol {\beta }})$ , är lika med

${\ displaystyle \eta _{j}(\mathbf {x} _{i};{\boldsymbol {\beta }})=ln[{\frac {\pi _{j}(\mathbf {x} _{i} ;{\boldsymbol {\beta }})}{\pi _{1}(\mathbf {x} _{i};{\boldsymbol {\beta }})}}]=\beta _{j0}+\ beta _{j1}x_{i1}+\ldots +\beta _{jp}x_{ip}}$

där $j=1,\ldots ,k-1$ och $i=1,\ldots ,n$ . Den uppskattade parametermatrisen ${\hat {\boldsymbol {\beta }}}$ för multinomial hyperbolastisk regression erhålls genom att maximera log-likelihood-funktionen. De maximala sannolikhetsuppskattningarna för parametermatrisen ${\boldsymbol {\beta }}$ är

${\boldsymbol {\hat {\beta }}}={\underset {\boldsymbol {\beta }}{\operatörsnamn {argmax} }}{\summa _ {i=1}^{n}(y_{i1}ln[\pi _{1}(\mathbf {x} _{i};{\boldsymbol {\beta }})]+y_{i2}ln[ \pi _{2}(\mathbf {x} _{i};{\boldsymbol {\beta }})]+\ldots +y_{ik}ln[\pi _{k}(\mathbf {x} _ {i};{\boldsymbol {\beta }})])}$