Homotopi förlängningsegenskap

I matematik , inom området för algebraisk topologi , indikerar homotopiförlängningsegenskapen vilka homotopier som definieras på ett delrum som kan utökas till en homotopi definierad på ett större utrymme . Homotopiförlängningsegenskapen för kofibreringar är dubbel mot den homotopilyftande egenskapen som används för att definiera fibrationer .

Definition

Låt $X\,\!$ vara ett topologiskt rum och låt $A\subset X$ . Vi säger att paret $(X,A)\,\!$ har egenskapen homotopy extension if, givet en homotopi $f_{\bullet }\colon A\rightarrow Y^{I}$ och en karta ${\tilde {f}}_{0}\colon X\rightarrow Y$ så att

$${\tilde {f}}_{0}\circ \iota =\left.{\tilde {f}}_{0}\right|_{A}= f_{0}=\pi _{0}\circ f_{\bullet },$$

då finns det en förlängning av $f_{\bullet }$ till en homotopi ${\tilde {f}}_{\bullet }\colon X\rightarrow Y^ {I}$ så att ${\tilde {f}}_{\bullet }\circ \iota =\left.{\tilde {f}}_{\bullet }\right|_{A}=f_{\ punkt }$ .

Det vill säga, paret $(X,A)\,\!$ har homotopitilläggsegenskapen om någon karta ${ \displaystyle G\colon ((X\times \{0\})\cup (A\times I))\rightarrow Y}$ kan utökas till en karta $G'\colon X\times I\rightarrow Y$ (dvs $G\,\!$ och $G'\,\!$ är överens om sin gemensamma domän).

Om paret endast har den här egenskapen för en viss koddomän $Y\,\!$ , säger vi att $(X,A)\,\!$ har egenskapen homotopy extension med respekt till $Y\,\!$ .

Visualisering

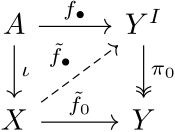
Homotopiförlängningsegenskapen visas i följande diagram

Om diagrammet ovan (utan den streckade kartan) pendlar (detta motsvarar villkoren ovan), så har paret (X,A) egenskapen homotopy extension om det finns en karta f ~ ∙ {\displaystyle {\ $} }_{\bullet }}$ vilket gör att diagrammet pendlar. Lägg märke till att homotopier uttryckta som kartor ${\tilde {f}}_{\bullet }\colon X\to Y^{I}$ är i naturlig bijektion med uttryck som kartor ${\tilde {f}}_{\bullet }\colon X\ gånger I\to Y$ .

Observera att detta diagram är dubbelt till (motsats till) det för homotopilyftegenskapen ; denna dualitet kallas löst som Eckmann–Hilton-dualitet .

Egenskaper

• Om $X\,\!$ är ett cellkomplex och $A\,\!$ är ett subkomplex av $X\,\!$ , då är paret ${ \displaystyle (X,A)\,\!}$ har egenskapen homotopy extension.
• Ett par $(X,A)\,\!$ har egenskapen homotopy extension if and only if $(X\times \{0\ }\cup A\times I)$ är en tillbakadragning av $X\times I.$

Övrig

Om $(X,A)$ har homotopiförlängningsegenskapen, så är den enkla inklusionskartan $\iota \colon A\to X$ en cofibration .

Faktum är att om du överväger någon samfibrering $\iota \colon Y\to Z$ , så har vi att $\mathbf {\mathit {Y}}$ är homeomorf till sin bild under $\iota$ . Detta innebär att alla samfibrer kan behandlas som en inklusionskarta och därför kan den behandlas som att den har egenskapen homotopiförlängning.

Se även

• Homotopi lyftegenskap

•   Hatcher, Allen (2002). Algebraisk topologi . Cambridge University Press. ISBN 0-521-79540-0 .
• "Homotopy extension property" . PlanetMath .