Hills muskelmodell

Inom biomekanik hänvisar Hills muskelmodell till antingen Hills ekvationer för tetaniserad muskelkontraktion eller till 3-elementsmodellen . De härleddes av den berömda fysiologen Archibald Vivian Hill .

Ekvation till tetaniserad muskel

Detta är en populär tillståndsekvation som är tillämplig på skelettmuskler som har stimulerats för att visa tetanisk sammandragning . Den relaterar spänning till hastighet med hänsyn till den inre termodynamiken . Ekvationen är

\left(v+b\right)(F+a)=b(F_{0}+a),\ qquad (1)

var

$F$ är spänningen (eller belastningen) i muskeln
$v$ är sammandragningshastigheten
$F_{0}$ är den maximala isometriska spänningen (eller belastningen) som genereras i muskeln
$a$ koefficient för förkortning av värme
$b=a\cdot v_{0}/F_{0}$
$v_{0}$ är den maximala hastigheten när $F=0$

Även om Hills ekvation ser väldigt mycket ut som van der Waals ekvation , har den förra enheter för energiförlust , medan den senare har enheter av energi . Hills ekvation visar att förhållandet mellan F och v är hyperboliskt . Därför, ju högre belastning som appliceras på muskeln, desto lägre blir kontraktionshastigheten. På samma sätt, ju högre sammandragningshastighet, desto lägre spänning i muskeln. Denna hyperboliska form har visat sig passa den empiriska konstanten endast under isotoniska sammandragningar nära vilolängden.

Muskelspänningen minskar när förkortningshastigheten ökar. Denna funktion har tillskrivits två huvudorsaker. Den stora tycks vara spänningsförlusten när tvärbryggorna överbryggar i det kontraktila elementet och sedan reformeras i ett förkortat tillstånd. Den andra orsaken verkar vara vätskeviskositeten i både det kontraktila elementet och bindväven. Oavsett orsaken till spänningsbortfallet är det en viskös friktion och kan därför modelleras som ett vätskespjäll .

Treelementsmodell

Muskellängd vs kraft. I Hills muskelmodell är de aktiva och passiva krafterna

F_{CE}

respektive

F_{PE}

.

Hills elastiska muskelmodell. F: Kraft; CE: Sammandragande element; SE: Serieelement; PE: Parallellt element.

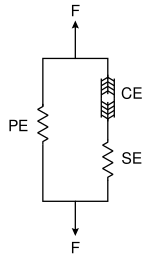
Hill -muskelmodellen med tre element är en representation av muskelmekanisk respons. Modellen består av ett kontraktilt element ( CE ) och två icke-linjära fjäderelement , ett i serie ( SE ) och ett annat parallellt ( PE ). Den aktiva kraften hos det kontraktila elementet kommer från kraften som genereras av aktin- och myosin -korsbryggorna på sarkomernivån . Den är helt utdragbar när den är inaktiv men kan förkortas när den är aktiverad. Bindvävnaderna ( fascia , epimysium , perimysium och endomysium ) som omger det kontraktila elementet påverkar muskelns kraftlängdskurva . Det parallella elementet representerar den passiva kraften hos dessa bindvävnader och har ett mjukdelsmekaniskt beteende. Det parallella elementet är ansvarigt för muskelpassivt beteende när det sträcks , även när det kontraktila elementet inte är aktiverat. Serieelementet representerar senan och myofilamentens inneboende elasticitet. Den har också en mjukvävnadsrespons och ger energilagringsmekanism.

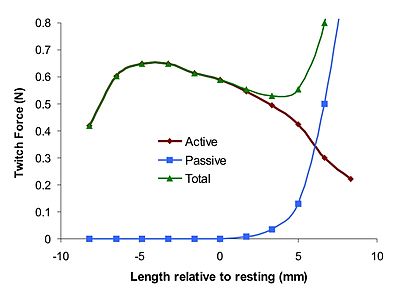
Nettokraft-längdegenskaperna för en muskel är en kombination av kraft-längdegenskaperna för både aktiva och passiva element. Krafterna i det kontraktila elementet, i serieelementet och i det parallella elementet, $F^{CE}$ , $F^{SE}$ och $F ^{PE}$ , respektive, tillfredsställa

F=F^{PE}+F^{SE},\qquad F^{CE}=F^{SE },\qquad (2)

Å andra sidan, muskellängden $L$ och längderna $L^{CE}$ , $L^{SE}$ och $L ^{PE}$ av dessa element uppfyller

L=L^{PE},\qquad L=L^{CE}+L^{SE},\qquad (3 )

Under isometriska sammandragningar är den elastiska komponenten i serie under spänning och sträcks därför en ändlig mängd. Eftersom muskelns totala längd hålls konstant, kan sträckningen av serieelementet endast ske om det sker en lika stor förkortning av själva kontraktila elementet.

Krafterna i de parallella, seriella och kontraktila elementen definieras av:

F^{PE}(\lambda _{f} )=F_{0}f^{PE}(\lambda _{f}),\qquad F^{SE}(\lambda ^{SE},\lambda ^{CE})=F_{0}f^{ SE}(\lambda ^{SE},\lambda ^{CE}),\qquad F^{CE}(\lambda ^{CE},{\dot {\lambda }}^{CE},a)=F_ {0}f_{L}^{CE}(\lambda ^{CE})f_{V}^{CE}({\dot {\lambda }}^{CE})a,\qquad (4)

där

{\textstyle \lambda _{f},\lambda _{CE}, \lambda _{SE}}

är töjningsmått för de olika elementen som definieras av:

\lambda _{f}={\frac {L}{L_{0}}} ,\quad \lambda ^{CE}={\frac {L^{CE}}{L_{0}}},\quad \lambda ^{SE}={\frac {L}{L^{CE}} },\qquad (5)

där

{\textstyle L}

är den deformerade muskellängden och

{\textstyle L^{CE}}

är den deformerade muskellängden på grund av rörelse av det kontraktila elementet, båda från ekvation (3).

{\textstyle L_{0}}

är muskelns vilolängd.

\lambda _{f}

kan delas som

{\textstyle \lambda _{f}=\lambda ^{SE}\lambda ^{CE}}

. Krafttermen,

F_{0}

, är den maximala isometriska muskelkraften och funktionerna

{\textstyle f^{PE},f ^{SE},f_{L}^{CE},f_{V}^{CE}}

ges av:

)

där $c,A$ är empiriska konstanter. Funktionen $a(t)$ från ekvation (4) representerar muskelaktiveringen. Den definieras utifrån den vanliga differentialekvationen:

{\frac {da(t)}{dt}}={\frac {1}{\tau _{rise}}}(1-a(t)u(t)+ {\frac {1}{\tau _{fall}}}(a_{min}-a(t))(1-u(t))),\qquad (10)

där

\tau _{rise},\tau _{fall}

är tidskonstanter relaterade till stigning och avklingning för muskelaktivering och

a_{ min}

är en minimigräns, allt bestämt från experiment.

u(t)

är den neurala excitation som leder till muskelkontraktion.

Viskoelasticitet

Muskler uppvisar viskoelasticitet , därför kan en viskös dämpare inkluderas i modellen när dynamiken i den andra ordningens kritiskt dämpade ryckningen beaktas. En vanlig modell för muskulär viskositet är en exponentiell formdämpare, där

F_{D}=k({\dot {L}}_{D})^{a},\qquad (11)

läggs till modellens globala ekvation, vars $k$ och $a$ är konstanter.

Se även

Muskelsammandragning

^ Hill, AV (oktober 1938). "Värmen av förkortning och dynamikkonstanter av muskler" . Proc. R. Soc. Lond. B . London: Royal Society. 126 (843): 136–195. doi : 10.1098/rspb.1938.0050 .
^ ^a ^b ^c ^d Fung, Y.-C. (1993). Biomekanik: Mekaniska egenskaper hos levande vävnader . New York: Springer-Verlag. sid. 568. ISBN 0-387-97947-6 .
^ Martins, JAC; Pires, EB; Salvado, R.; Dinis, PB (1998). "Numerisk modell för passivt och aktivt beteende hos skelettmuskler". Datormetoder i tillämpad mekanik och teknik . Elsevier. 151 (3–4): 419–433. Bibcode : 1998CMAME.151..419M . doi : 10.1016/S0045-7825(97)00162-X .
^ Pandy, Marcus G.; Zajac, Felix E.; Sim, Eunsup; Levine, William S. (1990-01-01). "En optimal kontrollmodell för människohoppning i maximal höjd" . Journal of Biomechanics . 23 (12): 1185–1198. doi : 10.1016/0021-9290(90)90376-E . ISSN 0021-9290 . PMID 2292598 .
^ Martins, JAC; Pato, MPM; Pires, EB (2006-09-01). "En finit elementmodell av skelettmuskler" . Virtuella och fysiska prototyper . 1 (3): 159–170. doi : 10.1080/17452750601040626 . ISSN 1745-2759 . S2CID 137665181 .

[Hill_1938-1] Hill, AV (oktober 1938). "Värmen av förkortning och dynamikkonstanter av muskler" . Proc. R. Soc. Lond. B . London: Royal Society. 126 (843): 136–195. doi : 10.1098/rspb.1938.0050 .

[Fung-2] Fung, Y.-C. (1993). Biomekanik: Mekaniska egenskaper hos levande vävnader . New York: Springer-Verlag. sid. 568. ISBN 0-387-97947-6 .

[Martins-3] Martins, JAC; Pires, EB; Salvado, R.; Dinis, PB (1998). "Numerisk modell för passivt och aktivt beteende hos skelettmuskler". Datormetoder i tillämpad mekanik och teknik . Elsevier. 151 (3–4): 419–433. Bibcode : 1998CMAME.151..419M . doi : 10.1016/S0045-7825(97)00162-X .

[4] Pandy, Marcus G.; Zajac, Felix E.; Sim, Eunsup; Levine, William S. (1990-01-01). "En optimal kontrollmodell för människohoppning i maximal höjd" . Journal of Biomechanics . 23 (12): 1185–1198. doi : 10.1016/0021-9290(90)90376-E . ISSN 0021-9290 . PMID 2292598 .

[5] Martins, JAC; Pato, MPM; Pires, EB (2006-09-01). "En finit elementmodell av skelettmuskler" . Virtuella och fysiska prototyper . 1 (3): 159–170. doi : 10.1080/17452750601040626 . ISSN 1745-2759 . S2CID 137665181 .