Hackenbush
Hackenbush är ett spel för två spelare som uppfanns av matematikern John Horton Conway . Den kan spelas på vilken konfiguration som helst av färgade linjesegment som är anslutna till varandra genom sina ändpunkter och till en "jordlinje".
Gameplay
Spelet börjar med att spelarna ritar en "mark"-linje (vanligtvis, men inte nödvändigtvis, en horisontell linje längst ner på tidningen eller annan spelyta) och flera linjesegment så att varje linjesegment är anslutet till marken, antingen direkt vid en ändpunkt, eller indirekt, via en kedja av andra segment sammankopplade med ändpunkter. Vilket antal segment som helst kan mötas vid en punkt och det kan därför finnas flera vägar till marken.
På sin tur "klipper" (raderar) en spelare valfritt linjesegment. Varje linjesegment som inte längre är anslutet till marken via någon väg "faller" (dvs. raderas). Enligt den normala spelkonventionen för kombinatorisk spelteori förlorar den första spelaren som inte kan röra sig.
Hackenbush-brädorna kan bestå av ändligt många (i fallet med en "ändlig bräda") eller oändligt många (i fallet med en "oändlig bräda") linjesegment. Förekomsten av ett oändligt antal linjesegment bryter inte mot det spelteoriska antagandet att spelet kan avslutas på en begränsad tid, förutsatt att det bara finns ändligt många linjesegment som direkt "vidrör" marken. På en oändlig bräda, baserat på brädets layout, kan spelet fortsätta för evigt, förutsatt att det finns oändligt många punkter som rör marken.
Varianter

I den ursprungliga folkloreversionen av Hackenbush tillåts vilken spelare som helst att skära vilken kant som helst: eftersom detta är ett opartiskt spel är det relativt enkelt att ge en fullständig analys med hjälp av Sprague-Grundy-satsen . Således är versionerna av Hackenbush av intresse för kombinatorisk spelteori mer komplexa partisanspel , vilket betyder att alternativen (dragen) som är tillgängliga för en spelare inte nödvändigtvis skulle vara de som är tillgängliga för den andra spelaren om det var deras tur att flytta givet samma position . Detta uppnås på ett av två sätt:
- Original Hackenbush: Alla linjesegment har samma färg och kan klippas av båda spelarna. Detta innebär att utbetalningarna är symmetriska och att varje spelare har samma operationer baserat på position ombord (i det här fallet ritningsstruktur)
- Blå-röd Hackenbush : Varje linjesegment är färgat antingen rött eller blått. En spelare (vanligtvis den första eller vänstra spelaren) får bara klippa blå linjesegment, medan den andra spelaren (vanligtvis den andra eller höger spelaren) bara får klippa röda linjesegment.
- Blå-röd-grön Hackenbush : Varje linjesegment är färgat rött, blått eller grönt. Reglerna är desamma som för Blue-Red Hackenbush, med den ytterligare bestämmelse att gröna linjesegment kan skäras av båda spelarna.
Blue-Red Hackenbush är bara ett specialfall av Blue-Red-Green Hackenbush, men det är värt att notera separat, eftersom analysen ofta är mycket enklare. Detta beror på att Blue-Red Hackenbush är ett så kallat kallt spel , vilket i huvudsak betyder att det aldrig kan vara en fördel att ha det första draget.
Analys
Hackenbush har ofta använts som ett exempelspel för att demonstrera definitioner och begrepp inom kombinatorisk spelteori, med början med dess användning i böckerna On Numbers and Games och Winning Ways for Your Mathematical Plays av några av grundarna av området. Speciellt Blue-Red Hackenbush kan användas för att konstruera surrealistiska tal : ändliga blå-röda Hackenbush-brädor kan konstruera dyadiska rationella tal , medan värdena på oändliga blå-röda Hackenbush-brädor står för reella tal , ordinaler och många fler allmänna värden som är varken. Blå-röd-grön Hackenbush gör det möjligt att bygga ytterligare spel vars värden inte är reella siffror, såsom stjärna och alla andra nimbers .
Ytterligare analys av spelet kan göras med hjälp av grafteori genom att betrakta brädan som en samling av hörn och kanter och undersöka vägarna till varje hörn som ligger på marken (vilket bör betraktas som en framstående hörn - det skadar inte att identifiera alla markpunkter tillsammans - snarare än som en linje på grafen).
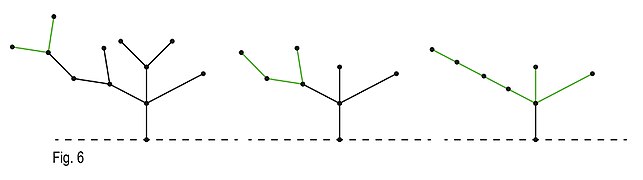
I den opartiska versionen av Hackenbush (den utan spelarspecifika färger) kan man tänka sig att använda nim heaps genom att dela upp spelet i flera fall: vertikalt, konvergent och divergent. Spelas uteslutande med vertikala högar av linjesegment, även kallade bambu stjälkar, blir spelet direkt Nim och kan direkt analyseras som sådant. Divergerande segment, eller träd, lägger till ytterligare en rynka till spelet och kräver användning av kolonprincipen som säger att när grenar möts i en vertex kan man ersätta grenarna med en icke-förgrenad stjälk med en längd lika med deras nim summa . Denna princip ändrar representationen av spelet till den mer grundläggande versionen av bambustjälkarna. Den sista möjliga uppsättningen grafer som kan göras är konvergenta, även kända som godtyckligt rotade grafer. Genom att använda fusionsprincipen kan vi konstatera att alla hörn på vilken cykel som helst kan smältas samman utan att grafens värde ändras. Därför kan vilken konvergent graf som helst också tolkas som en enkel graf av bambustjälk. Genom att kombinera alla tre typerna av grafer kan vi lägga till komplexitet till spelet, utan att någonsin ändra spelets nim summa, och därigenom tillåta spelet att ta Nims strategier.
Bevis på kolonprincipen
Kolonprincipen säger att när grenar samlas i en vertex kan man ersätta grenarna med en icke-grenad stjälk med längd lika med deras nim summa. Betrakta en fast men godtycklig graf, G , och välj en godtycklig vertex, x , i G . Låt H 1 och H 2 vara godtyckliga träd (eller grafer) som har samma Sprague-Grundy-värde. Betrakta de två graferna G 1 = G x : H 1 och G 2 = G x : H 2 , där G x : H i representerar grafen som konstruerats genom att fästa trädet H i till toppunkten x på grafen G . Kolonprincipen säger att de två graferna G1 och G2 har samma Sprague-Grundy-värde. Tänk på summan av de två spelen. Påståendet att G 1 och G 2 har samma Sprague-Grundy-värde är ekvivalent med påståendet att summan av de två spelen har Sprague-Grundy-värdet 0. Med andra ord ska vi visa att summan G 1 + G 2 är en P-position. En spelare är garanterad att vinna om de är den andra spelaren att flytta i G 1 + G 2 . Om den första spelaren rör sig genom att hugga en av kanterna i G i ett av spelen, så hugger den andra spelaren samma kant i G i det andra spelet. (Ett sådant par av drag kan ta bort H 1 och H 2 från spelen, men annars störs inte H 1 och H 2. ) Om den första spelaren rör sig genom att hugga en kant i H 1 eller H 2 , så är Sprague-Grundy värdena för H 1 och H 2 är inte längre lika, så att det finns en rörelse i H 1 eller H 2 som håller Sprague-Grundy-värdena desamma. På så sätt kommer du alltid att ha ett svar på varje rörelse han kan göra. Det betyder att du kommer att göra det sista draget och därmed vinna.
- John H. Conway, On Numbers and Games , 2:a upplagan, AK Peters, 2000.