Häxan från Agnesi

Valda häxor av Agnesi-kurvor (grön) och cirklarna de är konstruerade från (blå), med radieparametrar $a=1$ , $a=2$ , ${\ displaystyle a=4}$ och $a=8$ .

I matematik är häxan från Agnesi ( italienskt uttal: [aɲˈɲeːzi, -eːsi; -ɛːzi] ) en kubisk plan kurva definierad från två diametralt motsatta punkter i en cirkel. Den har fått sitt namn från den italienska matematikern Maria Gaetana Agnesi , och från en felöversättning av ett italienskt ord för ett seglingsblad . Före Agnesi studerades samma kurva av Fermat , Grandi och Newton .

Grafen för derivatan av arctangensfunktionen utgör ett exempel på häxan från Agnesi . Som sannolikhetstäthetsfunktion för Cauchy-fördelningen har häxan från Agnesi tillämpningar inom sannolikhetsteorin . Det ger också upphov till Runges fenomen i approximationen av funktioner med polynom, har använts för att approximera energifördelningen av spektrallinjer, och modellerar formen av kullar.

Häxan är tangent till sin definierande cirkel vid en av de två definierande punkterna och asymptotisk till tangentlinjen till cirkeln vid den andra punkten. Den har en unik vertex (en punkt med extrem krökning) vid tangenspunkten med dess definierande cirkel, som också är dess oskulerande cirkel vid den punkten. Den har också två ändliga böjningspunkter och en oändlig böjningspunkt. Arean mellan häxan och dess asymptotiska linje är fyra gånger arean av den definierande cirkeln, och rotationsvolymen för kurvan runt dess definierande linje är dubbelt så stor som volymen av rotationstorn för dess definierande cirkel .

Konstruktion

Häxan från Agnesi (kurva MP ) med märkta spetsar

En animation som visar konstruktionen av häxan från Agnesi

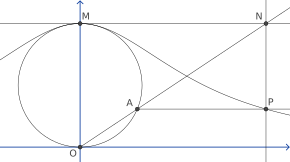
För att konstruera denna kurva, börja med två valfria punkter O och M och rita en cirkel med OM som diameter. För varje annan punkt A på cirkeln, låt N vara skärningspunkten för sekantlinjen OA och tangentlinjen vid M . Låt P vara skärningspunkten för en linje vinkelrät mot OM genom A och en linje parallell med OM genom N . Då P på häxan från Agnesi. Häxan består av alla punkter P som kan konstrueras på detta sätt från samma val av O och M . Den inkluderar, som ett begränsande fall, själva punkten M.

Ekvationer

Antag att punkt O är vid origo och punkt M ligger på den positiva $y$ -axeln, och att cirkeln med diametern OM har radien $a$ . Sedan har häxan konstruerad från O och M den kartesiska ekvationen

$$y={\frac {8a^{3}}{x^{2}+4a^{2}}}.$$

Denna ekvation kan förenklas genom att välja $a={\tfrac {1}{2}}$ till formuläret

$$y={\frac {1}{x^{2}+1}}.$$

eller motsvarande, genom att rensa nämnare , som den algebraiska kubiska ekvationen

$$(x^{2}+1)y=1.$$

I sin förenklade form är denna kurva grafen för derivatan av arctangensfunktionen .

Häxan från Agnesi kan också beskrivas med parametriska ekvationer vars parameter θ är vinkeln mellan OM och OA , mätt medurs:

$${\begin{aligned}x&=2a\tan \theta ,\\y&=2a\cos ^{2}\theta .\end{aligned}}$$

Egenskaper

De huvudsakliga egenskaperna för denna kurva kan härledas från integralkalkyl . Arean mellan häxan och dess asymptotiska linje är fyra gånger arean av den fasta cirkeln, $4\pi a^{2}$ . Rotationsvolymen för häxan från Agnesi om dess asymptot är $4\pi ^{2}a^{3$ . } Detta är två gånger volymen av torusen som bildas genom att rotera häxans definierande cirkel runt samma linje.

Kurvan har en unik vertex vid tangenspunkten med dess definierande cirkel. Det vill säga, denna punkt är den enda punkt där krökningen når ett lokalt minimum eller lokalt maximum. Häxans definierande cirkel är också dess oskulerande cirkel i spetsen, den unika cirkeln som "kyssar" kurvan vid den punkten genom att dela samma orientering och krökning. Eftersom detta är en oskulerande cirkel vid kurvans spets, har den tredje ordningens kontakt med kurvan.

Kurvan har två böjningspunkter vid punkterna

$$\left(\pm {\frac {2a}{\sqrt {3}}},{\frac {3a}{2}}\right)$$

motsvarande vinklarna $\theta =\pm \pi /6$ . När det betraktas som en kurva i det projektiva planet finns det också en tredje oändlig böjningspunkt, vid den punkt där linjen i oändligheten korsas av den asymptotiska linjen. Eftersom en av dess böjningspunkter är oändlig, har häxan det minsta möjliga antalet ändliga reella böjningspunkter för en icke-singular kubisk kurva.

Den största arean av en rektangel som kan skrivas in mellan häxan och dess asymptot är $4a^{2}$ , för en rektangel vars höjd är radien för den definierande cirkeln och vars bredd är två gånger diametern på cirkeln .

Historia

Tidiga studier

Agnesis illustration från 1748 av kurvan och dess konstruktion

Kurvan studerades av Pierre de Fermat i hans 1659 avhandling om kvadratur . I den beräknar Fermat arean under kurvan och hävdar (utan detaljer) att samma metod sträcker sig lika bra till Diocles cissoid . Fermat skriver att kurvan föreslogs för honom " ab erudito geometra " [av en lärd geometer]. Paradís, Pla & Viader (2008) spekulerar i att geometern som föreslog denna kurva för Fermat kan ha varit Antoine de Laloubère .

Den ovan angivna konstruktionen för denna kurva hittades av Grandi (1718) ; samma konstruktion hittades också tidigare av Isaac Newton , men publicerades först postumt senare, 1779. Grandi (1718) föreslog också namnet versiera (på italienska) eller versoria (på latin) för kurvan. Den latinska termen används också för ett ark , repet som vrider seglet, men Grandi kan istället ha haft för avsikt att bara referera till versusfunktionen som förekom i hans konstruktion.

År 1748 publicerade Maria Gaetana Agnesi Instituzioni analitiche ad uso della gioventù italiana , en tidig lärobok om kalkyl . I den, efter att först ha övervägt två andra kurvor, inkluderar hon en studie av denna kurva. Hon definierar kurvan geometriskt som platsen för punkter som uppfyller en viss proportion, bestämmer dess algebraiska ekvation och hittar dess vertex, asymptotiska linje och böjningspunkter.

Etymologi

Maria Gaetana Agnesi döpte kurvan enligt Grandi, versionra . Av en slump var det vid den tiden i Italien vanligt att tala om djävulen med andra ord som aversiero eller versiero , som härstammar från latinets adversarius , Guds "motståndare". Versiera , i synnerhet, användes för att indikera djävulens hustru, eller "häxan". På grund av detta översatte Cambridge-professorn John Colson namnet på kurvan som "häxa". Olika moderna verk om Agnesi och om kurvan föreslår lite olika gissningar hur exakt denna felöversättning hände. Struik nämner att:

Ordet [ versiera ] kommer från latinet vertere , att vända, men är också en förkortning av italienska avversiera , kvinnlig djävul. Vissa kvickheter i England översatte det en gång till "häxa", och den fåniga ordleken finns fortfarande kärleksfullt bevarad i de flesta av våra läroböcker på engelska. ... Kurvan hade redan förekommit i Fermats ( Oeuvres , I, 279–280; III, 233–234) och andras skrifter; namnet versiera kommer från Guido Grandi ( Quadratura circuli et hyperbolae , Pisa, 1703). Kurvan är typ 63 i Newtons klassificering. ... Den första att använda termen "häxa" i denna mening kan ha varit B. Williamson, Integral calculus , 7 (1875), 173; se Oxford English Dictionary .

Å andra sidan föreslår Stephen Stigler att Grandi själv "kan ha ägnat sig åt en lek med ord", en dubbel ordlek som kopplar djävulen till versus och sinusfunktionen till formen på det kvinnliga bröstet (som båda kan skrivas). som "seno" på italienska).

Ansökningar

En skalad version av kurvan är sannolikhetstäthetsfunktionen för Cauchy-fördelningen . Detta är sannolikhetsfördelningen på den slumpmässiga variabeln $x$ som bestäms av följande slumpmässiga experiment : för en fast punkt $p$ ovanför $x$ -axeln, välj slumpmässigt en linje genom $p$ , och låt $x$ vara koordinaten för den punkt där denna slumpmässiga linje korsar axeln. Cauchy-fördelningen har en toppfördelning som visuellt liknar normalfördelningen , men dess tunga svansar hindrar den från att ha ett förväntat värde enligt de vanliga definitionerna, trots dess symmetri. När det gäller själva häxan betyder detta att $x$ -koordinaten för tyngdpunkten i området mellan kurvan och dess asymptotiska linje inte är väldefinierad, trots denna regions symmetri och ändliga area.

I numerisk analys , när man approximerar funktioner med hjälp av polynominterpolation med jämnt fördelade interpolationspunkter, kan det vara fallet för vissa funktioner att användning av fler punkter skapar sämre approximationer, så att interpolationen avviker från funktionen den försöker approximera snarare än att konvergera till den . Detta paradoxala beteende kallas Runges fenomen . Den upptäcktes först av Carl David Tolmé Runge för Runges funktion ${\displaystyle y=1/(1+25x^{2})} ,$ en annan skalad version av häxan från Agnesi, vid interpolering av denna funktion över intervallet $[-1,1]$ . Samma fenomen inträffar för häxan $y=1/(1+x^{2})$ själv över det bredare intervallet $[- 5,5]$ .

Häxan från Agnesi närmar sig den spektrala energifördelningen av spektrallinjer , särskilt röntgenlinjer .

Tvärsnittet av en slät kulle har en liknande form som häxan. Kurvor med denna form har använts som det generiska topografiska hindret i ett flöde i matematisk modellering. Ensamma vågor på djupt vatten kan också ta denna form.

En version av denna kurva användes av Gottfried Wilhelm Leibniz för att härleda Leibniz formel för π . Denna formel, den oändliga serien

$${\frac {\pi }{4}}=1\,-\,{\frac {1}{3}} \,+\,{\frac {1}{5}}\,-\,{\frac {1}{7}}\,+\,{\frac {1}{9}}\,-\, \cdots ,$$

kan härledas genom att likställa arean under kurvan med integralen av funktionen $1/(1+x^{2})$ , med hjälp av Taylor-seriens expansion av denna funktion som oändlig geometrisk serie ${\displaystyle 1-x^{2}+x^{4}-x^{6}+\cdots } ,$ och integrera term-för-term.

I populärkulturen

Häxan från Agnesi är titeln på en roman av Robert Spiller. Den innehåller en scen där en lärare ger en version av terminens historia.

Witch of Agnesi är också titeln på ett musikalbum av jazzkvartetten Radius. Omslaget till albumet har en bild av häxans konstruktion.

externa länkar

• "Häxan från Agnesi" på MacTutor's Famous Curves Index
• Weisstein, Eric W. , "Häxan från Agnesi" , MathWorld
• Witch of Agnesi av Chris Boucher baserat på verk av Eric W. Weisstein , The Wolfram Demonstrations Project .
• "Häxan från Agnesi" vid "mathcurve"
• Lamb, Evelyn (28 maj 2018), "A Few of My Favorite Spaces: The Witch of Agnesi" , Roots of Unity , Scientific American