Fitts lag

Fitts lag: utkast till målstorlek W och avstånd till mål D

Fitts lag (ofta citerad som Fitts lag ) är en prediktiv modell av mänsklig rörelse som främst används i människa-datorinteraktion och ergonomi . Lagen att snabbt förflytta sig till ett målområde är en funktion av förhållandet mellan avståndet till målet och målets bredd. Fitts lag används för att modellera handlingen att peka , antingen genom att fysiskt röra ett föremål med en hand eller finger, eller virtuellt, genom att peka på ett föremål på en datorskärm med hjälp av en pekanordning . Det utvecklades ursprungligen av Paul Fitts .

Fitts lag har visat sig gälla under en mängd olika förhållanden; med många olika lemmar (händer, fötter, underläppen, huvudmonterade sikten), manipulanda (inmatningsenheter), fysiska miljöer (inklusive under vattnet) och användarpopulationer (unga, gamla, särskilda utbildningsbehov och drogade deltagare).

Original modellformulering

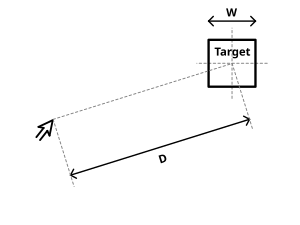
Den ursprungliga uppsatsen från 1954 av Paul Morris Fitts föreslog ett mått för att kvantifiera svårigheten med en målvalsuppgift. Måttet baserades på en informationsanalogi, där avståndet till mitten av målet ( D ) är som en signal och toleransen eller bredden på målet ( W ) är som brus. Mätvärdet är Fitts svårighetsindex ( ID , i bitar):

{\text{ID}}=\log _{2}{\Bigg (}{\frac {2D}{W}}{\Bigg )}

Passar uppgift från det ursprungliga experimentet

Fitts föreslog också ett prestandaindex ( IP , i bitar per sekund) som ett mått på mänsklig prestation. Mätvärdet kombinerar en uppgifts svårighetsindex ( ID ) med rörelsetiden ( MT , i sekunder) vid val av mål. Med Fitts ord, "Den genomsnittliga informationshastigheten som genereras av en serie rörelser är den genomsnittliga informationen per rörelse dividerat med tiden per rörelse." Således,

{\text{IP}}={\Bigg (}{\frac {\text{ID}}{\text{MT}}}{\Bigg )}

Idag kallas IP mer allmänt för genomströmning ( TP ). Det är också vanligt att ta med en justering för noggrannhet i beräkningen.

Forskare efter Fitts började praxis att bygga linjära regressionsekvationer och undersöka korrelationen ( r ) för god passform. Ekvationen uttrycker förhållandet mellan MT och uppgiftsparametrarna D och W :

{\text{MT}}=a+b\cdot {\text{ID}}=a+b\cdot \ log _{2}{\Bigg (}{\frac {2D}{W}}{\Bigg )}

Graf över det linjära sambandet mellan Fitts lagparametrar

var:

MT är den genomsnittliga tiden för att slutföra rörelsen.
a och b är konstanter som beror på valet av inmatningsenhet och bestäms vanligtvis empiriskt genom regressionsanalys . a definierar skärningspunkten på y- axeln och tolkas ofta som en fördröjning. Parametern b är en lutning och beskriver en acceleration. Båda parametrarna visar det linjära beroendet i Fitts lag.
ID är svårighetsindexet.
D är avståndet från startpunkten till mitten av målet.
W är bredden på målet mätt längs rörelseaxeln. W kan också betraktas som den tillåtna feltoleransen i slutpositionen, eftersom den sista punkten av rörelsen måste falla inom ± W ⁄ 2 från målets centrum.

Eftersom kortare rörelsetider är önskvärda för en given uppgift, kan värdet på parametern b användas som ett mått när man jämför datorpekdon mot varandra. Den första gränssnitt mellan människa och dator av Fitts lag var av Card, English och Burr, som använde prestandaindex ( IP ), tolkat som 1 ⁄ b , för att jämföra prestanda för olika inmatningsenheter , med musen ovanpå jämfört med joysticken eller riktningsrörelsetangenterna. Detta tidiga arbete, enligt Stuart Cards biografi, "var en viktig faktor som ledde till musens kommersiella introduktion av Xerox ".

Många experiment som testar Fitts lag tillämpar modellen på en datauppsättning där antingen avstånd eller bredd, men inte båda, varieras. Modellens prediktiva kraft försämras när båda varieras över ett betydande intervall. Observera att eftersom ID- termen endast beror på förhållandet mellan avstånd och bredd, innebär modellen att en kombination av målavstånd och bredd kan skalas om godtyckligt utan att påverka rörelsetiden, vilket är omöjligt. Trots sina brister har denna modell av modellen en anmärkningsvärd prediktiv kraft över en rad datorgränssnittsmodaliteter och motoruppgifter, och har gett många insikter i användargränssnittsdesignprinciper.

Rörelse

En rörelse under en enda Fitts laguppgift kan delas upp i två faser:

initial rörelse . En snabb men oprecis rörelse mot målet
sista rörelsen . Långsammare men mer exakt rörelse för att nå målet

Den första fasen definieras av avståndet till målet. I denna fas kan avståndet stängas snabbt samtidigt som det fortfarande är oprecist. Den andra rörelsen försöker utföra en långsam och kontrollerad exakt rörelse för att faktiskt träffa målet. Uppgiftens varaktighet skalas linjärt med avseende på svårighetsgrad. Men eftersom olika uppgifter kan ha samma svårighet, härleds det att avståndet har en större inverkan på den totala uppgiftens slutförandetid än målstorleken.

Ofta citeras det att Fitts lag kan tillämpas på eyetracking . Detta verkar åtminstone vara ett kontroversiellt ämne som Drewes visade. Under snabba saccadiska ögonrörelser är användaren blind. Under en Fitts lag-uppgift förvärvar användaren medvetet sitt mål och kan faktiskt se det, vilket gör dessa två typer av interaktion inte jämförbara.

Bitar per sekund: modellinnovationer drivna av informationsteori

Formuleringen av Fitts svårighetsindex som oftast används i människa-datorinteraktionsgemenskapen kallas Shannon-formuleringen:

{\text{ID}}=\log _{2}{\Bigg (}{\frac {D}{W}}+1{\Bigg )}

Denna form föreslogs av Scott MacKenzie, professor vid York University , och namngavs för dess likhet med Shannon-Hartley-satsen . Den beskriver överföringen av information med hjälp av bandbredd, signalstyrka och brus. I Fitts lag representerar avståndet signalstyrkan, medan målbredden är brus.

Genom att använda denna modell av modellen likställdes svårigheten med en pekuppgift med en mängd information som överfördes (i bitenheter) genom att utföra uppgiften. Detta motiverades med påståendet att pekande reducerar till en informationsbehandlingsuppgift. Även om ingen formell matematisk koppling etablerades mellan Fitts lag och Shannon-Hartley-satsen som den inspirerades av, har Shannon-formen av lagen använts flitigt, troligen på grund av överklagandet av att kvantifiera motoriska handlingar med hjälp av informationsteori. 2002 publicerades ISO 9241 , som tillhandahåller standarder för testning av gränssnitt mellan människa och dator, inklusive användningen av Shannon-formen av Fitts lag. Det har visat sig att informationen som överförs via seriella tangenttryckningar på ett tangentbord och informationen som antyds av ID för en sådan uppgift inte är konsekventa. Shannon-entropin resulterar i ett annat informationsvärde än Fitts lag. Författarna noterar dock att felet är försumbart och endast måste beaktas i jämförelser av enheter med känd entropi eller mätningar av mänsklig informationsbehandlingskapacitet.

Justering för noggrannhet: användning av den effektiva målbredden

En viktig förbättring av Fitts lag föreslogs av Crossman 1956 (se Welford, 1968, s. 147–148) och användes av Fitts i hans artikel från 1964 med Peterson. Med justeringen ersätts målbredd ( W ) av en effektiv målbredd ( W _e ). W _e beräknas från standardavvikelsen i urvalskoordinaterna samlade över en sekvens av försök för ett speciellt DW- tillstånd. Om valen loggas som x -koordinater längs inflygningsaxeln till målet, då

W_{e}=4.133\times SD_{x}

Detta ger

{\text{ID}}_{e}=\log _{2}{\Bigg (}{\frac {D}{W_{e} }}+1{\Bigg )}

och följaktligen

{\text{IP}}={\Bigg (}{\frac {ID_{e}}{MT}}{\Bigg )}

Om urvalskoordinaterna är normalfördelade spänner W _e över 96 % av fördelningen. Om den observerade felfrekvensen var 4 % i försökssekvensen, så är W _e = W . Om felfrekvensen var större än 4 %, W _e > W , och om felfrekvensen var mindre än 4 %, W _e < W . Genom att använda W _e återspeglar en Fitts lagmodell närmare vad användarna faktiskt gjorde, snarare än vad de ombads att göra.

Den största fördelen med att beräkna IP enligt ovan är att rumslig variabilitet, eller noggrannhet, ingår i mätningen. Med justeringen för noggrannhet, omfattar Fitts lag mer verkligen avvägningen mellan hastighet och noggrannhet. Ekvationerna ovan visas i ISO 9241-9 som den rekommenderade metoden för beräkning av genomströmning .

Welfords modell: innovationer drivna av prediktiv kraft

Inte långt efter att den ursprungliga modellen föreslogs, föreslogs en 2-faktorsvariation under intuitionen att målavstånd och bredd har separata effekter på rörelsetiden. Welfords modell, som föreslogs 1968, separerade inflytandet av målavstånd och bredd i separata termer och gav förbättrad prediktiv kraft:

T=a+b_{1}\log _{2}(D)+b_{2}\log _{ 2}(W)

Denna modell har en extra parameter, så dess prediktiva noggrannhet kan inte direkt jämföras med 1-faktorformer av Fitts lag. Men en variant på Welfords modell inspirerad av Shannon-formuleringen,

T=a+b_{1}\log _{2}(D+W)+b_{2}\log _{2}(W)=a+b\log _{2}\left({\frac {D+W}{W^{k} }}\höger)

Den extra parametern k tillåter införandet av vinklar i modellen. Nu kan användarnas position redovisas. Vinkelns inverkan kan viktas med hjälp av exponenten. Detta tillägg introducerades av Kopper et al. år 2010.

Formeln reduceras till Shannon-formen när k = 1 . Därför kan denna modell direkt jämföras med Shannon-formen av Fitts lag med F-testet av kapslade modeller. Denna jämförelse avslöjar att inte bara Shannon-formen av Welfords modell bättre förutsäger rörelsetider, utan den är också mer robust när kontroll-displayförstärkning (förhållandet mellan t.ex. handrörelse och markörrörelse) varieras. Följaktligen, även om Shannon-modellen är något mer komplex och mindre intuitiv, är den empiriskt den bästa modellen att använda för virtuella pekuppgifter.

Utöka modellen från 1D till 2D och andra nyanser

Förlängningar till två eller flera dimensioner

I sin ursprungliga form är Fitts lag menad att endast gälla endimensionella uppgifter. Emellertid krävde de ursprungliga experimenten att försökspersonerna flyttade en penna (i tre dimensioner) mellan två metallplattor på ett bord, kallad den ömsesidiga knakningsuppgiften. Målbredden vinkelrätt mot rörelseriktningen var mycket bred för att undvika att den skulle ha en betydande inverkan på prestandan. En viktig tillämpning för Fitts lag är virtuella pekuppgifter i 2D på datorskärmar, där mål har avgränsade storlekar i båda dimensionerna.

Ömsesidig tappuppgift i 2D-sammanhang

Fitts lag har utvidgats till tvådimensionella uppgifter på två olika sätt. För navigering av t.ex. hierarkiska rullgardinsmenyer måste användaren generera en bana med pekdonet som är begränsad av menygeometrin; för denna applikation härleddes Accot-Zhais styrlag .

För att helt enkelt peka på mål i ett tvådimensionellt utrymme, håller modellen i allmänhet som den är men kräver justeringar för att fånga målgeometri och kvantifiera målfel på ett logiskt konsekvent sätt. Flera metoder kan användas för att bestämma målstorleken:

status Quo: målets horisontella bredd
summamodell: W är lika med höjd + bredd
områdesmodell: W är lika med höjd * bredd
mindre av modellen: W mindre värde på höjd och bredd
W-modell: W är den effektiva bredden i rörelseriktningen

Totalt sett representerar W -modellen den senaste mätningen.

Karakteriserande prestanda

Eftersom a- och b -parametrarna bör fånga rörelsetider över ett potentiellt brett spektrum av uppgiftsgeometrier, kan de fungera som prestandamått för ett givet gränssnitt. Därvid är det nödvändigt att skilja variation mellan användare från variation mellan gränssnitt. Parametern a är vanligtvis positiv och nära noll, och ignoreras ibland när den karakteriserar medelprestanda, som i Fitts ursprungliga experiment. Det finns flera metoder för att identifiera parametrar från experimentella data, och valet av metod är föremål för het debatt, eftersom metodvariationer kan resultera i parameterskillnader som överväldigar underliggande prestationsskillnader.

En ytterligare fråga för att karakterisera prestanda är att införliva framgångsfrekvensen: en aggressiv användare kan uppnå kortare rörelsetider till priset av experimentella försök där målet missas. Om de senare inte är inkorporerade i modellen, kan genomsnittliga rörelsetider minskas på konstgjord väg.

Temporära mål

Fitts lag behandlar endast mål som definieras i rymden. Ett mål kan dock definieras rent på tidsaxeln, vilket kallas ett temporalt mål. Ett blinkande mål eller ett mål som rör sig mot ett urvalsområde är exempel på tidsmässiga mål. _{I likhet}_med rymden kan avståndet till målet (dvs. temporalt avstånd Dt ) och målets bredd (dvs. temporal bredd Wt ) också definieras för temporala mål. Det tidsmässiga avståndet är hur lång tid en person måste vänta på att ett mål ska dyka upp. Den tidsmässiga bredden är en kort varaktighet från det ögonblick målet dyker upp tills det försvinner. Till exempel, för ett blinkande mål, D _t ses som blinkningsperioden och W _t som varaktigheten av blinkningen. Precis som med mål i rymden, ju större D _t eller ju mindre W _{t är} , desto svårare blir det att välja målet.

Uppgiften att välja det tidsmässiga målet kallas temporal pekning . Modellen för temporal pekning presenterades först för interaktionsfältet människa–dator 2016. Modellen förutsäger felfrekvensen, den mänskliga prestandan vid temporal pekning, som en funktion av temporalt svårighetsindex ( ID _t ):

{\text{ID}}_{t}=\log _{2}{\Bigg (}{\frac {D_{t}}{W_{ t}}}{\Bigg )}

Implikationer för UI-design

Magiska hörn i Microsoft Windows

Radiell meny

Flera designriktlinjer för GUI kan härledas från konsekvenserna av Fitts lag. I sin grundform säger Fitts lag att mål som en användare måste träffa ska vara så stora som möjligt. Detta härleds från W- parametern. Mer specifikt bör den effektiva storleken på knappen vara så stor som möjligt, vilket innebär att dess form måste optimeras för riktningen för användarens rörelse mot målet.

Layouter bör också klustera funktioner som ofta används med varandra. Optimering för D -parametern på detta sätt möjliggör kortare restider.

Att placera layoutelement på skärmens fyra kanter möjliggör oändligt stora mål i en dimension och presenterar därför idealiska scenarier. Eftersom pekaren alltid stannar vid kanten kan användaren flytta musen med största möjliga hastighet och ändå träffa målet. Målområdet är effektivt oändligt långt längs rörelseaxeln. Därför kallas denna riktlinje "Regeln för de oändliga kanterna". Användningen av denna regel kan ses till exempel i MacOS , som alltid placerar menyraden i den övre vänstra kanten av skärmen istället för det aktuella programmets fönsterram.

Denna effekt kan överdrivas i de fyra hörnen av en skärm. Vid dessa punkter kolliderar två kanter och bildar en teoretiskt oändligt stor knapp. Microsoft Windows (före Windows 11 ) placerar sin "Start"-knapp i det nedre vänstra hörnet och Microsoft Office 2007 använder det övre vänstra hörnet för sin "Office"-meny. Dessa fyra fläckar kallas ibland "magiska hörn". MacOS placerar stängningsknappen på den övre vänstra sidan av programfönstret och menyraden fyller ut det magiska hörnet med en annan knapp.

Ett användargränssnitt som tillåter popup-menyer snarare än fasta rullgardinsmenyer minskar restiderna för D -parametern. Användaren kan fortsätta interaktionen direkt från den aktuella muspositionen och behöver inte flytta till ett annat förinställt område. Många operativsystem använder detta när de visar högerklickskontextmenyer. Eftersom menyn startar precis på den pixel som användaren klickade på, kallas denna pixel för "magic" eller "prime pixel".

James Boritz et al. (1991) jämförde radiella menydesigner . I en radiell meny har alla objekt samma avstånd från den primära pixeln. Forskningen tyder på att i praktiska implementeringar måste man också ta hänsyn till riktningen i vilken en användare måste flytta sin mus. För högerhänta användare var det betydligt svårare att välja menyalternativet längst till vänster än det som låg längst till höger. Inga skillnader hittades för övergångar från övre till nedre funktioner och vice versa.

Se även

Bibliografi

Accot, Johnny; Zhai, Shumin (2002). Mer än att pricka i:en – grunderna för korsningsbaserade gränssnitt . Proceedings of ACM CHI 2002 Conference on Human Factors in Computing Systems . s. 73–80. doi : 10.1145/503376.503390 . ISBN 978-1581134537 .
Accot, Johnny; Zhai, Shumin (2003). Förfina Fitts lagmodeller för bivariat pekning . Proceedings of ACM CHI 2003 Conference on Human Factors in Computing Systems . s. 193–200. doi : 10.1145/642611.642646 . ISBN 978-1581136302 .
Card, Stuart K.; Moran, Thomas P.; Newell, Allen (1983). Psykologin för människa–datorinteraktion . Hillsdale, NJ: L. Erlbaum Associates. ISBN 978-0898592436 .
Fitts, Paul M.; Peterson, James R. (februari 1964). "Informationskapacitet för diskreta motorsvar". Journal of Experimental Psychology . 67 (2): 103–112. doi : 10.1037/h0045689 . PMID 14114905 .

externa länkar

En interaktiv visualisering av Fitts lag med JavaScript och D3 av Simon Wallner
Fitts' Law vid CS-avdelningen NSF-stödd utbildningsinfrastrukturprojekt
Fitts' lag: modellering av rörelsetid i HCI
Bibliografi över Fitts' Law Research sammanställd av I. Scott MacKenzie
Fitts' Law Software – Gratis nedladdning av I. Scott MacKenzie
En frågesport designad för att ge dig passform av Bruce Tognazzini