Fishers metod

Under Fishers metod kombineras två små p-värden P ₁ och P _{2 för att bilda ett mindre p-värde.} Den mörkaste gränsen definierar den region där metaanalysens p-värde är under 0,05. Till exempel, om båda p-värdena är runt 0,10, eller om det ena är runt 0,04 och det andra är runt 0,25, är metaanalysens p-värde runt 0,05.

₀ Inom statistik är Fishers metod , även känd som Fishers kombinerade sannolikhetstest , en teknik för datafusion eller " metaanalys " (analys av analyser). Den har utvecklats av och uppkallad efter Ronald Fisher . I sin grundläggande form används den för att kombinera resultaten från flera oberoende tester som bygger på samma övergripande hypotes ( H ).

Ansökan till oberoende teststatistik

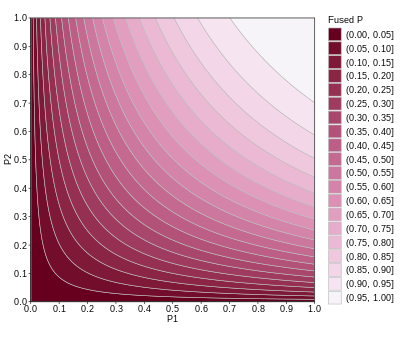
Fishers metod kombinerar extremvärdessannolikheter från varje test, allmänt känt som " p-värden ", till en teststatistik ( X ² ) med hjälp av formeln

$X_{2k}^{2}\sim -2\sum _{i=1}^{k}\log(p_ {i}),$

där p _i är p-värdet för det i: ^te hypotestestet. När p-värdena tenderar att vara små blir teststatistiken X ² stor, vilket tyder på att nollhypoteserna inte är sanna för varje test.

När alla nollhypoteser är sanna, och pi (eller deras motsvarande teststatistik) är oberoende, har X ² en chi-kvadratfördelning med 2 k frihetsgrader , där k är antalet test som kombineras _. Detta faktum kan användas för att bestämma p-värdet för X ² .

Fördelningen av X ² är en chi-kvadratfördelning av följande anledning; under nollhypotesen för test i följer p-värdet p _i en enhetlig fördelning på intervallet [0,1]. Den negativa logaritmen för ett enhetligt fördelat värde följer en exponentialfördelning . Att skala ett värde som följer en exponentiell fördelning med en faktor två ger en kvantitet som följer en chi-kvadratfördelning med två frihetsgrader. Slutligen följer summan av k oberoende chi-kvadratvärden, var och en med två frihetsgrader, en chi-kvadratfördelning med 2 k frihetsgrader.

Begränsningar av oberoende antagande

Beroendet bland statistiska tester är generellt positivt, vilket innebär att p-värdet för X ² är för litet (antikonservativt) om beroendet inte beaktas. Således, om Fishers metod för oberoende tester tillämpas i en beroende miljö, och p-värdet inte är tillräckligt litet för att förkasta nollhypotesen, kommer den slutsatsen att fortsätta att gälla även om beroendet inte är korrekt redogjort för. Men om positivt beroende inte redovisas och metaanalysens p-värde visar sig vara litet, är bevisen mot nollhypotesen i allmänhet överskattade. Den genomsnittliga falska upptäcktsfrekvensen , $\alpha (k+1)/(2k)$ , $\alpha$ reducerad för k oberoende eller positivt korrelerade tester, kan räcker för att kontrollera alfa för användbar jämförelse med ett för litet p-värde från Fisher's X ² .

Utökning till beroende teststatistik

Huvudartikel: Förlängningar av Fishers metod

I de fall där testerna inte är oberoende är nollfördelningen av X ² mer komplicerad. En vanlig strategi är att approximera nollfördelningen med en skalad χ ² -fördelningsslumpvariabel . Olika tillvägagångssätt kan användas beroende på om kovariansen mellan de olika p-värdena är känd eller inte.

Browns metod kan användas för att kombinera beroende p-värden vars underliggande teststatistik har en multivariat normalfördelning med en känd kovariansmatris. Kosts metod utökar Browns till att tillåta en att kombinera p-värden när kovariansmatrisen är känd endast upp till en skalär multiplikativ faktor.

Det harmoniska medelvärdet p -värde erbjuder ett alternativ till Fishers metod för att kombinera p -värden när beroendestrukturen är okänd men testerna inte kan antas vara oberoende.

Tolkning

Fishers metod tillämpas vanligtvis på en samling oberoende teststatistik, vanligtvis från separata studier med samma nollhypotes. Metaanalysens nollhypotes är att alla separata nollhypoteser är sanna. Metaanalysalternativhypotesen är att åtminstone en av de separata alternativa hypoteserna är sann.

I vissa sammanhang är det vettigt att överväga möjligheten till "heterogenitet", där nollhypotesen gäller i vissa studier men inte i andra, eller där olika alternativa hypoteser kan gälla i olika studier. En vanlig orsak till den senare formen av heterogenitet är att effektstorlekar kan skilja sig åt mellan populationer. Överväg till exempel en samling medicinska studier som tittar på risken för en diet med hög glukos för att utveckla typ II- diabetes . På grund av genetiska eller miljömässiga faktorer kan den verkliga risken förknippad med en given nivå av glukoskonsumtion vara större i vissa mänskliga populationer än i andra.

I andra sammanhang är den alternativa hypotesen antingen universellt falsk eller universell sann – det finns ingen möjlighet att den håller i vissa sammanhang men inte i andra. Tänk till exempel på flera experiment utformade för att testa en viss fysisk lag. Eventuella skillnader mellan resultaten från separata studier eller experiment måste bero på slumpen, möjligen driven av skillnader i makt .

Vid en metaanalys med tvåsidiga test är det möjligt att förkasta metaanalysens nollhypotes även när de enskilda studierna visar starka effekter i olika riktningar. I det här fallet förkastar vi hypotesen att nollhypotesen är sann i varje studie, men detta innebär inte att det finns en enhetlig alternativ hypotes som gäller för alla studier. Sålunda är dubbelsidig metaanalys särskilt känslig för heterogenitet i de alternativa hypoteserna. Ensidig metaanalys kan upptäcka heterogenitet i effektstorlekarna, men fokuserar på en enda, fördefinierad effektriktning.

Relation till Stouffers Z-score-metod

Sambandet mellan Fishers metod och Stouffers metod kan förstås utifrån förhållandet mellan z och −log( p )

Ett närbesläktat tillvägagångssätt till Fishers metod är Stouffers Z, baserat på Z-poäng snarare än p-värden, vilket möjliggör inkorporering av studievikter. Den är uppkallad efter sociologen Samuel A. Stouffer . Om vi ​​låter Z _i = Φ ^{− 1} (1− p _i ), där Φ är den normala kumulativa normalfördelningsfunktionen , då

$Z\sim {\frac {\sum _{i=1}^{k}Z_{i}}{\sqrt {k}}},$

är ett Z-värde för den övergripande metaanalysen. Denna Z-poäng är lämplig för ensidiga högersidiga p-värden; mindre modifieringar kan göras om tvåsidiga eller vänstersidiga p-värden analyseras. , används det tvåsidiga p-värdet (pi _{/ 2) eller 1- pi} om vänstersvansade p-värden används.

Eftersom Fishers metod är baserad på medelvärdet av −log( p _i )-värden och Z-score-metoden är baserad på medelvärdet av Z _i- värdena, följer förhållandet mellan dessa två tillvägagångssätt av förhållandet mellan z och −log( p ) = −log(1− Φ ( z )). För normalfördelningen är dessa två värden inte perfekt linjärt relaterade, men de följer ett mycket linjärt samband över det intervall av Z-värden som oftast observeras, från 1 till 5. Som ett resultat är kraften i Z-poängmetoden nästan identisk med kraften i Fishers metod.

En fördel med Z-score-metoden är att det är enkelt att införa vikter. Om den i: ^te Z-poängen viktas med w _i , är Z-poängen för metaanalysen

$Z\sim {\frac {\sum _{i=1}^{k}w_{i}Z_{i} }{\sqrt {\sum _{i=1}^{k}w_{i}^{2}}}},$

som följer en standardnormalfördelning under nollhypotesen. Medan viktade versioner av Fishers statistik kan härledas, blir nollfördelningen en viktad summa av oberoende chi-kvadratstatistik, vilket är mindre bekvämt att arbeta med.

Se även

• Förlängningar av Fishers metod
• En alternativ källa till Fishers anteckning från 1948: [1]
• Fishers, Stouffers Z-poäng och några relaterade metoder är implementerade i metap R-paketet.