Faro blanda

Faro shuffle (amerikansk), weave shuffle (brittisk) eller dovetail shuffle är en metod för att blanda spelkort , där hälften av kortleken hålls i varje hand med tummarna inåt, sedan släpps korten med tummarna så att de falla till bordet interfolierat. Diaconis, Graham och Kantor kallar detta också tekniken när den används i magi.

Jämförelse av en perfekt faro out-shuffle och in-shuffle, siffrorna anger varje korts positioner före shuffle

Matematiker använder termen "faro shuffle" för att beskriva en exakt omarrangering av en kortlek i två lika högar med 26 kort som sedan är sammanvävda perfekt.

Beskrivning

En högerhänt utövare håller korten uppifrån i vänster hand och underifrån i höger hand. Kortleken delas upp i två helst lika delar genom att helt enkelt lyfta upp halva korten med höger tumme något och skjuta vänsterhands paket framåt bort från höger hand. De två paketen korsas ofta och knackas mot varandra för att rikta in dem. De skjuts sedan ihop på kortsidorna och böjs antingen uppåt eller nedåt. Korten faller sedan omväxlande på varandra, helst omväxlande ett och ett från varje halva, ungefär som en dragkedja . En flourish kan läggas till genom att fjädra ihop paketen genom att applicera tryck och böja dem uppifrån.

Ett spel Faro slutar med korten i två lika högar som dealern måste kombinera för att dela ut dem till nästa spel. Enligt trollkarlen John Maskelyne användes ovanstående metod, och han kallar den för "faro dealer's shuffle". Maskelyne var den första som gav tydliga instruktioner, men blandningen användes och associerades med faro tidigare, vilket mestadels upptäcktes av matematikern och magikern Persi Diaconis .

Perfekta blandningar

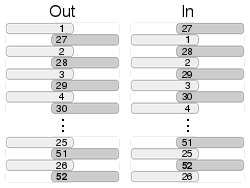
En faro-shuffle som lämnar det ursprungliga övre kortet överst och det ursprungliga bottenkortet längst ner kallas en out-shuffle , medan en som flyttar det ursprungliga övre kortet till andra och det ursprungliga bottenkortet till andra från botten är känt som en in-shuffle . Dessa namn myntades av magikern och dataprogrammeraren Alex Elmsley . En perfekt faro shuffle, där korten är perfekt alternerade, kräver att shufflern skär kortleken i två lika högar och lägger precis rätt tryck när de trycker halvlekarna in i varandra.

Faro shuffle är en kontrollerad shuffle som inte helt randomiserar ett kortlek. Om man kan göra perfekta in-shuffles, kommer 26 shuffles att vända ordningen på kortleken och 26 till kommer att återställa den till sin ursprungliga ordning.

I allmänhet kommer $k$ perfekta in-shuffles att återställa ordningen för en $n$ -kortlek om $2^{k}\equiv 1 {\pmod {n+1}}$ . Till exempel, 52 på varandra följande in-shuffles återställer ordningen för en kortlek med 52 kort, eftersom $2^{52}\equiv 1{\pmod {53}}$ .

I allmänhet kommer $k$ perfekta ut-shuffles att återställa ordningen för en $n$ -kortlek om $2^{k}\equiv 1 {\pmod {n-1}}$ . Till exempel, om man lyckas utföra åtta ut-shuffles i rad, kommer kortleken med 52 kort att återställas till sin ursprungliga ordning, eftersom 2 8 ≡ 1 ( mod 51 ) $1 {\pmod {51}}}$ . Det krävs dock bara 6 faro out-shuffles för att återställa ordningen för en kortlek med 64 kort.

Med andra ord, antalet shufflar som krävs för att returnera en kortlek av jämn storlek N till ursprunglig ordning ges av multiplikationsordningen 2 modulo ( N + 1).

Till exempel, för en kortleksstorlek på N = 2, 4, 6, 8, 10, 12 ..., är antalet blandningar som behövs: 2, 4, 3, 6, 10, 12, 4, 8, 18 , 6, 11, ... (sekvens A002326 i OEIS ).

Enligt Artins gissningar om primitiva rötter , följer det att det finns oändligt många däckstorlekar som kräver hela uppsättningen av n shuffles.

Den analoga operationen med en ut-shuffle för en oändlig sekvens är interfolieringssekvensen .

Exempel

För enkelhetens skull kommer vi att använda en kortlek med sex kort.

Följande visar ordningen på kortleken efter varje i shuffle av en in-shuffle. Lägg märke till att en kortlek av den här storleken återgår till sin ursprungliga ordning efter 3 omgångar.

Steg	Toppkort _	2	3	4	5	Nedre kort
Börja
1
2
3

Följande visar ordningen på kortleken efter varje utblandning. Lägg märke till att en kortlek av denna storlek återgår till sin ursprungliga ordning efter 4 omgångar.

Steg	Toppkort _	2	3	4	5	Nedre kort
Börja
1
2
3
4

Som däcksmanipulation

Magikern Alex Elmsley upptäckte ^{[ citat behövs ]} att en kontrollerad serie in- och ut-shufflar kan användas för att flytta det översta kortet i kortleken ner till vilken position som helst. Tricket är att uttrycka kortets önskade position som ett binärt tal , och sedan göra en in-shuffle för varje 1 och en ut-shuffle för varje 0.

Till exempel, för att flytta det översta kortet nedåt så att det finns tio kort ovanför det, uttryck talet tio binärt (1010 ₂ ). Blanda in, ut, in, ut. Dela ut tio kort från toppen av leken; det elfte kommer att vara ditt ursprungliga kort. Observera att det inte spelar någon roll om du uttrycker talet tio som 1010 ₂ eller 00001010 ₂ ; preliminära utblandningar kommer inte att påverka resultatet eftersom utblandningar alltid håller det översta kortet överst.

Gruppteoretiska aspekter

Inom matematiken kan en perfekt blandning betraktas som en del av den symmetriska gruppen .

Mer allmänt, i ${\displaystyle S_{2n}} är$ den perfekta blandningen permutationen som delar upp setet i 2 högar och interfolierar dem:

S_{2n}

=

{\begin{pmatrix}1&2&3&4&\cdots &2n -1&2n\\1&n+1&2&n+2&\cdots &n&2n\end{pmatrix}}

Det är med andra ord kartan

k\mapsto {\begin{cases}{\frac {k+1}{2}}&k\ {\text{udda}}\\ n+{\frac {k}{2}}&k\ {\text{even}}\end{case}}

Analogt är $(k,n)$ -perfekt shuffle-permutation elementet i $S_{kn}$ som delar upp mängden i k högar och interfolierar dem.

( $(2,n)$ -perfekt shuffle, betecknad $\rho _{n}$ , är sammansättningen av $,n-1)}$ ${\displaystyle (2$ -perfekt blandning med en $n$ -cykel, så tecknet för $\rho _{n}$ är:

{\mbox{sgn}}(\rho _{n})=(-1)^{n+1}{\mbox{sgn}}(\rho _{n-1}).

Tecknet är alltså 4-periodiskt:

{\mbox{sgn}}(\ rho _{n})=(-1)^{\lfloor n/2\rfloor }={\begin{cases}+1&n\equiv 0,1{\pmod {4}}\\-1&n\equiv 2, 3{\pmod {4}}\end{cases}}

De första perfekta shufflingarna är: $\rho _{0}$ och $\rho _{1}$ är triviala, och $\rho _{2}$ är transponeringen $(23)\in S_{4}$ .

Anteckningar

Diaconis, P .; Graham, RL ; Kantor, WM (1983). "Mathematics of perfect shuffles" (PDF) . Framsteg inom tillämpad matematik . 4 (2): 175–196. doi : 10.1016/0196-8858(83)90009-X .

Ellis, J.; Fan, H.; Shallit, J. (2002). "The Cycles of the Multiway Perfect Shuffle Permutation" (PDF) . Diskret matematik och teoretisk datavetenskap . 5 : 169-180. doi : 10.46298/dmtcs.308 . Hämtad 26 dec 2013 .

Maskelyne, John (1894). Sharps and Flats: A Complete Revelation of the Secrets of Cheating at Games of Chance and Skicklighet . Longmans, Green och Company . Hämtad 26 dec 2013 .

Morris, S. Brent (1998). Magiska trick, kortblandning och dynamiska datorminnen . The Mathematical Association of America. ISBN 0-883-85527-5 . Hämtad 26 dec 2013 .

Kolata, Gina (april 1982). "Perfekta blandningar och deras förhållande till matematik". Vetenskap . 216 (4545): 505–506. Bibcode : 1982Sci...216..505K . doi : 10.1126/science.216.4545.505 . PMID 17735734 .
Jain, Peiyush (maj 2008). "En enkel in-place algoritm för i shuffles". arXiv : 0805.1598 [ cs.DS ].