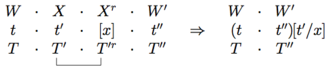Förgrupps grammatik
Pregroup grammatik (PG) är en grammatikformalism som är intimt relaterad till kategorigrammatik . Ungefär som kategoriserad grammatik (CG), är PG en typ av logisk grammatik. Till skillnad från CG har PG dock ingen framstående funktionstyp. Snarare använder PG inversa typer i kombination med dess monoidala drift.
Definition av en förgrupp
En förgrupp är en delvis ordnad algebra såsom att är en monoid , som uppfyller följande relationer:
- sammandragning)
- (expansion)
Sammandragnings- och expansionsförhållandena kallas ibland Ajdukiewicz- lagar.
Av detta kan det bevisas att följande ekvationer håller:
och kallas vänster respektive höger adjoint till x .
Symbolen och skrivs också respektive . I kategoriteorin är förgrupper också kända som autonoma kategorier eller (icke-symmetriska) kompakta slutna kategorier . Mer typiskt bara att representeras av adjacency, dvs som .
Definition av en förgruppsgrammatik
En förgruppsgrammatik består av ett lexikon av ord (och möjligen morfem ) L , en uppsättning atomtyper T som fritt genererar en förgrupp, och en relation som relaterar ord till typer. I enkla förgruppsgrammatiker är skrivning en funktion som mappar ord till endast en typ vardera.
Exempel
Några enkla, intuitiva exempel som använder engelska som språk för att modellera demonstrerar kärnprinciperna bakom förgrupper och deras användning i språkliga domäner.
0 Låt L = { John, Mary, the, dog, cat, meet, barked, at }, låt T = { N, S, N } och låt följande skrivrelation gälla:
En mening S som har typ T sägs vara grammatisk om . Vi kan bevisa detta genom att använda en kedja av . Till exempel kan vi bevisa att är grammatisk genom att bevisa att :
genom att först använda kontraktion på och sedan igen på . En mer bekväm notation finns dock som indikerar sammandragningar genom att koppla dem med en dragen länk mellan de sammandragande typerna (förutsatt att länkarna är kapslade, dvs inte korsar). Ord placeras också vanligtvis ovanför deras typer för att göra beviset mer intuitivt. Samma bevis i denna notation är helt enkelt
Ett mer komplext exempel bevisar att hunden som skällde på katten är grammatisk:
Historiska anteckningar
Pregroup grammatik introducerades av Joachim Lambek 1993 som en utveckling av hans syntaktiska kalkyl , och ersatte kvoterna med adjoints. Sådana adjoints hade redan använts tidigare av Harris men utan itererade adjoints och expansionsregler. Att lägga till sådana adjoints var intressant för att hantera mer komplexa språkliga fall, där det faktum att behövs. Det motiverades också av en mer algebraisk synpunkt: definitionen av en förgrupp är en försvagning av den för en grupp , introducerar en distinktion mellan vänster och höger invers och ersätter jämlikheten med en ordning. Denna försvagning behövdes eftersom att använda typer från en fri grupp inte skulle fungera: ett adjektiv skulle få typen därför skulle det kunna infogas vid någon position i meningen.
Förgruppsgrammatik har sedan definierats och studerats för olika språk (eller fragment av dem) inklusive engelska , italienska , franska , persiska och sanskrit . Språk med en relativt fri ordföljd som sanskrit krävs för att introducera kommuteringsrelationer till förgruppen, med precyklicitet.
Semantik av förgruppsgrammatik
På grund av bristen på funktionstyper i PG är den vanliga metoden att ge en semantik via λ-kalkylen eller via funktionsbeteckningar inte tillgänglig på något självklart sätt. Istället finns det två olika metoder, en rent formell metod som motsvarar λ-kalkylen och en denotationsmetod analog med (ett fragment av) kvantmekanikens tensormatematik .
Rent formell semantik
Den rent formella semantiken för PG består av ett logiskt språk definierat enligt följande regler:
- Givet en uppsättning atomtermer T = { a , b , ...} och atomfunktionssymboler F = { f m , g n , ...} (där nedsänkta är meta-notation som indikerar aritet), och variabler x , y , ..., alla konstanter, variabler och välformade funktionsapplikationer är grundläggande termer (en funktionsapplikation är välformad när funktionssymbolen appliceras på lämpligt antal argument, som kan dras från atomtermerna, variabler , eller kan vara andra grundläggande termer)
- Varje grundläggande term är en term
- Givet vilken variabel x som helst är [ x ] en term
- Givet alla termer m och n , är en term
Några exempel på termer är f ( x ), g ( a , h ( x , y )), . En variabel x är fri i en term t om [ x ] inte förekommer i t , och en term utan fria variabler är en sluten term. Termer kan skrivas med förgruppstyper på det självklara sättet.
De vanliga konventionerna för α-konvertering gäller.
För ett givet språk ger vi en uppgift I som mappar maskinskrivna ord till maskinskrivna slutna termer på ett sätt som respekterar typernas förgruppsstruktur. För det engelska fragmentet som ges ovan kan vi därför ha följande uppgift (med den uppenbara, implicita uppsättningen atomtermer och funktionssymboler):
där E är typen av entiteter i domänen och T är typen av sanningsvärden.
Tillsammans med denna kärndefinition av PGs semantik har vi också reduktionsregler som används parallellt med typreduktionerna. Att placera de syntaktiska typerna överst och semantiken nedan har vi
Till exempel att tillämpa detta på typerna och semantiken för meningen )
meningen :
Se även
- Lambek, Joachim (2008). "Förgruppsgrammatiker och Chomskys tidigaste exempel" (PDF) . Tidskrift för logik, språk och information . 17 (2): 141–160. doi : 10.1007/s10849-007-9053-2 . S2CID 30256603 .
- Preller, Anna (2007). "Semantiska förgruppsgrammatiker hanterar långdistansberoenden på franska" ( PDF) . Manuskript .
- Claudia Casadio (2004), Pregroup Grammar. Teori och tillämpningar

























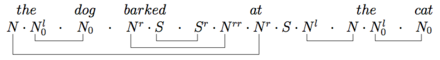



![{\displaystyle g(x,b)\cdot [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ce53e0e3d974fc6117121c92c6819a6febcb224)
![{\displaystyle {\begin{aligned}I({\textit {John}}:N)&=j:E\\I({\textit {Mary}}:N)&=m:E\\I(the:N\cdot N_{0}^{l})&=\iota (p)\cdot [p]:E\cdot E_{0}^{l}\\I(dog:N_{0})&=dog:E_{0}\\I(cat:N_{0})&=cat:E_{0}\\I(met:N^{r}\cdot S\cdot N^{l})&=[x]\cdot met(x,y)\cdot [y]:E^{r}\cdot T\cdot E^{l}\\I(barked:N^{r}\cdot S)&=[x]\cdot barked(x):E^{r}\cdot T\\I(at:S^{r}\cdot N^{rr}\cdot N^{r}\cdot S\cdot N^{l})&=[x]\cdot y\cdot [y]\cdot at(x,z)\cdot [z]:T^{r}\cdot E^{rr}\cdot E^{r}\cdot T\cdot E^{l}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e2cb7086fccdf1ee47d46f5a2a3e45273417225)