Euklidiskt minimumspännande träd

Euklidiskt minimumspännande träd med 25 slumpmässiga punkter i planet

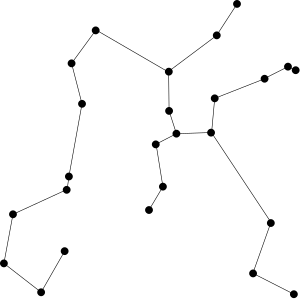
Ett euklidiskt minimumspännande träd av en ändlig uppsättning punkter i det euklidiska planet eller högre dimensionellt euklidiskt utrymme förbinder punkterna med ett system av linjesegment med punkterna som ändpunkter, vilket minimerar segmentens totala längd. I den kan två valfria punkter nå varandra längs en väg genom linjesegmenten. Det kan hittas som det minsta spännträdet i en komplett graf med punkterna som hörn och de euklidiska avstånden mellan punkter som kantvikter.

Kanterna på det minsta spännande trädet möts i vinklar på minst 60°, högst sex till en vertex. I högre dimensioner begränsas antalet kanter per vertex av det kyssande antalet tangentenhetssfärer . Den totala längden av kanterna, för punkter i en enhetskvadrat , är högst proportionell mot kvadratroten ur antalet punkter. Varje kant ligger i ett tomt område av planet, och dessa regioner kan användas för att bevisa att det euklidiska minimumspännande trädet är en subgraf av andra geometriska grafer inklusive den relativa grannskapsgrafen och Delaunay-trianguleringen . Genom att konstruera Delaunay-trianguleringen och sedan tillämpa en graf-minimumspännande trädalgoritm, kan det minsta spännträdet av $n$ givna plana punkter hittas i tiden $O(n\log n )$ , som uttrycks i stor O-notation . Detta är optimalt i vissa beräkningsmodeller, även om det finns snabbare randomiserade algoritmer för punkter med heltalskoordinater. För punkter i högre dimensioner är det fortfarande ett öppet problem att hitta en optimal algoritm .

Definition och relaterade problem

Ett euklidiskt minimumspännande träd, för en uppsättning av $n$ punkter i det euklidiska planet eller euklidiska rymden , är ett system av linjesegment , som endast har de givna punkterna som ändpunkter, vars förening inkluderar alla punkter i en ansluten uppsättning , och som har minsta möjliga totala längd av ett sådant system. Ett sådant nätverk kan inte innehålla en polygonal ring av segment; om en sådan fanns kunde nätverket förkortas genom att ta bort en kant på polygonen. Därför bildar nätverket med minsta längd ett träd . Denna observation leder till den ekvivalenta definitionen att ett euklidiskt minimumspännande träd är ett träd av linjesegment mellan par av de givna punkterna, med minsta totala längd. Samma träd kan också beskrivas som ett minimumspännande träd i en viktad komplett graf , med de givna punkterna som sina hörn och avstånden mellan punkter som kantvikter. Samma punkter kan ha mer än ett minsta spännträd. Till exempel, för hörn av en vanlig polygon , ger en borttagning av valfri kant på polygonen ett minsta spännträd.

Publikationer om det euklidiska minimumspännande trädet förkortar det vanligtvis som "EMST". De kan också kallas "geometriska minimumspännande träd", men den termen kan användas mer generellt för geometriska utrymmen med icke-euklidiska avstånd, såsom L ^p utrymmen . När sammanhanget för euklidiska punktuppsättningar är tydligt kan de helt enkelt kallas "minimumspännande träd".

Flera andra geometriska standardnätverk är nära besläktade med det euklidiska minimumspännande trädet:

• Steinerträdsproblemet söker återigen ett system av linjesegment som förbinder alla givna punkter, men utan att kräva att segmenten endast börjar och slutar vid givna punkter . I detta problem kan ytterligare punkter läggas till som segmentslutpunkter, vilket gör att Steiner-trädet kan vara kortare än det minsta spännträdet.
• I problemet med den euklidiska resande försäljarens väg måste de anslutande linjesegmenten börja och sluta vid de givna punkterna, som spännträdet och till skillnad från Steinerträdet; dessutom kan varje punkt vidröra högst två linjesegment, så resultatet bildar en polygonal kedja . På grund av denna begränsning kan den optimala vägen vara längre än det euklidiska minimumspännande trädet, men är högst dubbelt så lång.
• Geometriska skiftnycklar är lågviktsnätverk som, precis som det minsta spännträdet, förbinder alla punkter. Till skillnad från det minsta spännträdet måste alla dessa förbindningsvägar vara korta och ha en längd som är proportionell mot avståndet mellan punkterna de förbinder. För att uppnå denna egenskap har dessa nätverk i allmänhet cykler och så är det inte träd.

Egenskaper

Vinklar och vertexgrader

Tolv enhetssfärer tangerar alla en central enhetssfär. Minsta spännträd av deras 13 mittpunkter har grad 12 i mittpunkten.

Närhelst två kanter av ett euklidiskt minimumspännande träd möts i en vertex, måste de bilda en vinkel på 60° eller mer, med likhet endast när de bildar två sidor av en liksidig triangel . Detta beror på att för två kanter som bildar en skarpare vinkel kan en av de två kanterna ersättas med den tredje, kortare kanten av triangeln de bildar, vilket bildar ett träd med mindre total längd. Som jämförelse har Steinerträdproblemet en starkare vinkelgräns: ett optimalt Steinerträd har alla vinklar minst 120°.

Samma 60° vinkelgräns förekommer också i kyssnummerproblemet , att hitta det maximala antalet enhetssfärer i det euklidiska rymden som kan tangera en central enhetssfär utan att två sfärer skär varandra (bortom en tangenspunkt). Mittpunkterna av dessa sfärer har ett minimum som spänner över träd i form av en stjärna , med mittpunkten intill alla andra pekar. Omvänt, för vilken vertex $v$ som helst i ett minimumspännande träd, kan man konstruera icke-överlappande enhetssfärer centrerade vid $v$ och vid punkter två enheter längs var och en av dess kanter, med en tangens för varje granne av $v$ . Därför, i $n$ -dimensionellt utrymme är den maximala möjliga graden av en vertex (antalet spännande trädkanter kopplade till den) lika med det kyssande antalet sfärer i $n$ dimensioner. Planar minimumspännande träd har grad som högst sex, och när ett träd har grad sex finns det alltid ett annat minimumspännande träd med maximal grad fem. Tredimensionella minimumspännande träd har högst grad tolv. De enda högre dimensionerna där det exakta värdet av kyssnumret är känt är fyra, åtta och 24 dimensioner.

För punkter som genereras slumpmässigt från en given kontinuerlig fördelning är det minsta spännträdet nästan säkert unikt. Antalet hörn av en given grad konvergerar, för ett stort antal hörn, till en konstant gånger det antal hörn. Värdena på dessa konstanter beror på graden och fördelningen. Men även för enkla fall - som antalet blad för punkter som är likformigt fördelade i en kvadratisk enhet - är deras exakta värden inte kända.

Tomma regioner

Tomma områden för det euklidiska minimumspännande trädet: För den röda kanten som visas kan dessa regioner inte innehålla några andra hörn av trädet. Vit: den tomma linsen som definierar den relativa grannskapsgrafen . Ljusblå: diametercirkeln som definierar Gabriel-grafen och bildar en tom cirkel för Delaunay-trianguleringen . Mörkblå: en 60°–120° romb som inte kan överlappa med romber från andra spännande trädkanter.

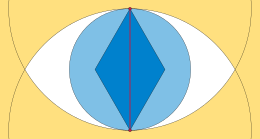
För vilken kant $uv$ som helst på ett euklidiskt minimumspännande träd, bildas linsen (eller vesica piscis ) genom att skära de två cirklarna med $uv$ eftersom deras radier inte kan ha någon annan given vertex ${\ displaystyle w}$ i dess interiör. Uttryckt på ett annat sätt, om något träd har en kant $uv$ vars lins innehåller en tredje punkt $w$ , så är det inte av minsta längd. För, med de två cirklarnas geometri, $w$ vara närmare både $u$ och $v$ än de är varandra. Om edge $uv$ togs bort från trädet, skulle $w$ förbli ansluten till en av $u$ och $v$ , men inte den andra. Att ersätta den borttagna kanten $uv$ med $uw$ eller $vw$ (vilken av dessa två kanter som återansluter $w$ till vertexet från vilken den kopplades bort) skulle producera ett kortare träd.

För varje kant $uv$ på ett euklidiskt minimumspännande träd, är romben med vinklar på 60° och 120°, med $uv$ som sin långa diagonal, skild från romben som bildas analogt av alla andra kanter. Två kanter som delar en ändpunkt kan inte ha överlappande romber, eftersom det skulle innebära en kantvinkel skarpare än 60°, och två disjunkta kanter kan inte ha överlappande romber; om de gjorde det, kunde den längre av de två kanterna ersättas med en kortare kant bland samma fyra hörn.

Supergrafer

Vissa geometriska grafer har definitioner som involverar tomma områden i punktuppsättningar, av vilka det följer att de innehåller varje kant som kan vara en del av ett euklidiskt minimumspännande träd. Dessa inkluderar:

• Den relativa grannskapsgrafen , som har en kant mellan valfritt par av punkter när linsen de definierar är tom.
• Gabriel -grafen , som har en kant mellan valfritt par av punkter när cirkeln med paret som diameter är tom.
• Delaunay -trianguleringen , som har en kant mellan valfritt par av punkter när det finns en tom cirkel med paret som ett ackord.
• Urquhart -grafen , bildad från Delaunay-trianguleringen genom att ta bort den längsta kanten av varje triangel. För varje återstående kant kan hörnen på Delaunay-trianglarna som använder den kanten inte ligga inom den tomma lunen i den relativa grannskapsgrafen.

Eftersom kriterierna för tomma regioner för dessa grafer blir allt svagare, bildar dessa grafer en ordnad sekvens av subgrafer. Det vill säga, med hjälp av "⊆" för att beteckna delmängdsrelationen mellan deras kanter, har dessa grafer relationerna:

Euklidiskt minimumspännande träd ⊆ relativ grannskapsgraf ⊆ Urquhart-graf ⊆ Gabriel-graf ⊆ Delaunay-triangulering.

En annan graf som garanterat innehåller det minsta spännträdet är Yao-grafen , som bestäms för punkter i planet genom att dela upp planet runt varje punkt i sex 60°-kilar och koppla varje punkt till närmaste granne i varje kil. Den resulterande grafen innehåller den relativa grannskapsgrafen, eftersom två hörn med en tom lins måste vara de närmaste grannarna till varandra i sina kilar. Som med många av de andra geometriska graferna ovan kan denna definition generaliseras till högre dimensioner, och (till skillnad från Delaunay-trianguleringen) inkluderar dess generaliseringar alltid ett linjärt antal kanter.

Total längd

För $n$ punkter i enhetens kvadrat (eller någon annan fast form), är den totala längden av de minsta spännande trädkanterna $O({\sqrt {n}})$ . Vissa uppsättningar av punkter, som punkter jämnt fördelade i ett ${\sqrt {n}}\times {\sqrt {n}}$ rutnät, uppnår denna gräns. För punkter i en enhetshyperkub i $d$ -dimensionellt utrymme är motsvarande gräns $O(n^{(d-1)/d})$ . Samma gräns gäller för den förväntade totala längden av det minsta spännträdet för $n$ punkter valda enhetligt och oberoende från en enhetskvadrat eller enhetshyperkub. Om vi ​​återgår till enhetskvadraten är summan av kvadratiska kantlängder för det minsta spännträdet $O(1)$ . Denna gräns följer av observationen att kanterna har disjunkta romber, med arean proportionell mot kantlängderna i kvadrat. O $O({\sqrt {n}})$ bunden till total längd följs av tillämpning av Cauchy– -olikheten .

En annan tolkning av dessa resultat är att den genomsnittliga kantlängden för varje uppsättning punkter i en enhetskvadrat är ${\displaystyle O(1/{\sqrt {n}})} ,$ högst proportionell mot avståndet av punkter i ett vanligt rutnät; och att för slumpmässiga punkter i en enhetskvadrat är medellängden proportionell mot $1/{\sqrt {n}}$ . Men i det slumpmässiga fallet, med hög sannolikhet, har den längsta kanten ungefär en längd

$${\sqrt {\frac {\log n}{\pi n}}},$$

längre än genomsnittet med en icke-konstant faktor. Med hög sannolikhet bildar den längsta kanten ett blad av det spännande trädet, och förbinder en punkt långt från alla andra punkter till sin närmaste granne. För ett stort antal punkter konvergerar fördelningen av den längsta kantlängden runt dess förväntade värde till en Laplace-fördelning .

Varje geometrisk skiftnyckel , en subgraf av en komplett geometrisk graf vars kortaste vägar approximerar det euklidiska avståndet, måste ha en total kantlängd som är minst lika stor som det minsta spännträdet, och ett av standardkvalitetsmåtten för en geometrisk skiftnyckel är förhållandet mellan dess total längd och minsta spännträd för samma punkter. Flera metoder för att konstruera nycklar, såsom den giriga geometriska nyckeln , uppnår en konstant gräns för detta förhållande. Det har antagits att Steiner-kvoten , det största möjliga förhållandet mellan den totala $\displaystyle 2/{\sqrt { 3}}\approx 1,1547}$ av ett minsta spännträd och Steiner-trädet för samma uppsättning punkter i planet, är , förhållandet för tre punkter i en liksidig triangel .

Indelning

Om varje kant av ett euklidiskt minimumspännande träd delas upp, genom att lägga till en ny punkt vid dess mittpunkt, är det resulterande trädet fortfarande ett minimumspännande träd i den utökade punktuppsättningen. Genom att upprepa denna indelningsprocess kan ett euklidiskt minimumspännande träd delas upp godtyckligt fint. Emellertid kan uppdelning av endast några av kanterna, eller uppdelning av kanterna vid andra punkter än mittpunkten, producera en punktuppsättning för vilken det uppdelade trädet inte är det minsta spännträdet.

Beräkningskomplexitet

För punkter i vilken dimension som helst, kan det minsta överspänningsträdet konstrueras i tiden $O(n^{2})$ genom att konstruera en komplett graf med en kant mellan varje par av punkter, viktat med euklidiskt avstånd , och sedan tillämpa en graf-minimumspännande trädalgoritm som Prim–Dijkstra–Jarník-algoritmen eller Borůvkas algoritm på den. Dessa algoritmer kan fås att ta tid $O(n^{2})$ på kompletta grafer, till skillnad från ett annat vanligt val, Kruskals algoritm , som är långsammare eftersom den involverar sortering av alla avstånd. För punkter i lågdimensionella utrymmen kan problemet lösas snabbare, som beskrivs nedan.

Att beräkna euklidiska avstånd involverar en kvadratrotsberäkning . I varje jämförelse av kantvikter ger en jämförelse av kvadraterna på de euklidiska avstånden, istället för själva avstånden, samma ordning, och ändrar därför inte resten av trädets beräkning. Den här genvägen påskyndar beräkningen och tillåter att ett minsta spännträd för punkter med heltalskoordinater konstrueras med enbart heltalsaritmetik.

Två dimensioner

Ett snabbare tillvägagångssätt för att hitta det minsta spännande trädet av plana punkter använder egenskapen att det är en subgraf av Delaunay-trianguleringen:

1. Beräkna Delaunay-trianguleringen, vilket kan göras i $O(n\log n)$ tid. Eftersom Delaunay-trianguleringen är en plan graf , har den högst $3n-6$ kanter.
2. Märk varje kant med dess (fyrkantiga) längd.
3. Kör en graf med minsta spännträdsalgoritm. Eftersom det finns ${\displaystyle O(n)}-$ kanter, kräver detta ${\displaystyle O(n\log n)}-$ tid med någon av de standardmässiga minimumspännande trädalgoritmerna.

Resultatet är en algoritm som tar $O(n\log n)$ tid, optimal i vissa beräkningsmodeller (se nedan ).

Om indatakoordinaterna är heltal och kan användas som arrayindex , är snabbare algoritmer möjliga: Delaunay-trianguleringen kan konstrueras av en randomiserad algoritm i $O(n\log \log n )$ förväntad tid. Dessutom, eftersom Delaunay-trianguleringen är en plan graf , kan dess minsta spännträd hittas i linjär tid av en variant av Borůvkas algoritm som tar bort alla utom den billigaste kanten mellan varje par av komponenter efter varje steg i algoritmen. Därför är den totala förväntade tiden för denna algoritm $O(n\log \log n)$ . I den andra riktningen kan Delaunay-trianguleringen konstrueras från det minsta spännande trädet i den närmast linjära tidsgränsen ${\displaystyle O(n\log ^{*}n)} ,$ där $\log ^{*}$ anger den itererade logaritmen .

Högre dimensioner

Problemet kan också generaliseras till $n$ punkter i $d$ -dimensionella rymden $\mathbb {R} ^{d}$ . I högre dimensioner innehåller anslutningsmöjligheten som bestäms av Delaunay-trianguleringen (som på samma sätt delar upp det konvexa skrovet i $d$ -dimensional simplices ) det minsta spännträdet; trianguleringen kan dock innehålla hela grafen. Att därför hitta det euklidiska minimumspännande trädet som ett spännträd i hela grafen eller som ett spännträd i Delaunay-trianguleringen tar båda $O(dn^{2})$ tid. För tre dimensioner kan det minsta spännträdet hittas i tiden $O{\bigl (}(n\log n)^{4/3}{\bigr )}$ , och i någon större dimension, i tid

$$O\left(n^{2-{\frac {2}{\lceil d/2\rceil +1}}+\varepsilon } \höger)$$

för alla $\varepsilon >0$ —snabbare än den kvadratiska tidsgränsen för hela grafen och Delaunays trianguleringsalgoritmer.

Den optimala tidskomplexiteten för träd med högre dimensioner är fortfarande okänd, men är nära relaterad till komplexiteten i att beräkna bikromatiska närmaste par . I det bikromatiska närmaste parproblemet är inmatningen en uppsättning punkter, givet två olika färger (säg, röd och blå). Utgången är ett par av en röd punkt och en blå punkt med minsta möjliga avstånd. Detta par bildar alltid en av kanterna i det minsta spännträdet. Därför kan problemet med det bikromatiska närmaste paret lösas under den tid det tar att konstruera ett minsta spännträd och skanna dess kanter efter den kortaste röd-blå kanten. Omvänt, för varje röd-blå färgning av någon delmängd av en given uppsättning punkter, producerar det bikromatiska närmaste paret en kant av det minsta spännträdet i delmängden. Genom att noggrant välja en sekvens av färger av delmängder och hitta det bikromatiska närmaste paret för varje delproblem, kan det minsta spännträdet hittas i tid proportionell mot den optimala tiden för att hitta bikromatiskt närmaste par för samma antal punkter, oavsett den optimala tiden visar sig att vara.

För likformigt slumpmässiga punktuppsättningar i vilken avgränsad dimension som helst, har Yao-grafen eller Delaunay-trianguleringen linjärt förväntat antal kanter, garanteras innehålla minsta spännträd och kan konstrueras i linjär förväntad tid. Från dessa grafer kan det minsta spännträdet självt konstrueras i linjär tid, genom att använda en randomiserad linjär tidsalgoritm för grafen av minsta spännträd . Dessa metoders dåliga prestanda på indata som kommer från klustrade data har dock fått inom algoritmteknik att utveckla metoder med en något långsammare $O(n\log n)$ tidsgräns, för slumpmässiga indata eller indata vars avstånd och klustring liknar de för slumpmässiga data, samtidigt som de uppvisar bättre prestanda på verkliga data.

En väl separerad parupplösning är en familj av par av delmängder av de givna punkterna, så att varje par av punkter tillhör ett av dessa par av delmängder, och så att alla par av punkter som kommer från samma par av delmängder har ungefär samma längd. Det är möjligt att hitta en väl separerad parupplösning med ett linjärt antal delmängder, och ett representativt punkterpar för varje delmängd, i tiden $O(n\log n)$ . Det minsta spännträdet i grafen som bildas av dessa representativa par är då en approximation till det minsta spännträdet. Med hjälp av dessa idéer kan en $(1+\varepsilon )$ -approximation till det minsta spännträdet hittas i $O(n\log n)$ tid , för konstant $\varepsilon$ . Mer exakt, genom att välja varje representativt par för att approximera det närmaste paret i dess ekvivalensklass, och noggrant variera kvaliteten på denna approximation för olika par, kan beroendet av $\varepsilon$ i tidsgränsen ges som $O(n\log n+(\varepsilon ^{-2}\log ^{2}{\tfrac {1}{\varepsilon }})n),$ för vilken fast dimension som helst.

Dynamisk och kinetisk

Det euklidiska minimumspännande trädet har generaliserats på många olika sätt till system med rörliga eller föränderliga punkter:

• Om en uppsättning punkter genomgår en sekvens av dynamiska infogningar eller raderingar av punkter, inducerar var och en av dessa uppdateringar en begränsad mängd förändringar av punkternas minsta spännträd. När uppdateringssekvensen är känd i förväg, för punkter i planet, kan förändringen efter varje infogning eller radering hittas i tid $O(\log ^{2}n)$ per infogning eller radering. När uppdateringarna måste hanteras online är en långsammare (men fortfarande polylogaritmisk) $O(\log ^{10}n)$ tidsgräns känd. För högre dimensionella versioner av problemet är tiden per uppdatering långsammare, men fortfarande sublinjär.
• För $n$ punkter som rör sig linjärt med konstant hastighet, eller med mer allmänna algebraiska rörelser, kommer det minsta spännträdet att ändras med en sekvens av byten, där en kant tas bort och en annan ersätter den vid en tidpunkt där båda ha lika långa. För linjära rörelser är antalet ändringar som mest något större än $displaystyle n^{25/9}$ \ För mer allmänna algebraiska rörelser finns det en nästan kubisk övre gräns för antalet byten, baserat på teorin om Davenport-Schinzel-sekvenser .
• det minsta rörliga spännträdet gäller återigen punkter som rör sig linjärt med konstant hastighet, över ett tidsintervall, och söker ett enda träd som minimerar den maximala summan av vikter som inträffar vid vilket ögonblick som helst under detta intervall. Det är NP-svårt att beräkna exakt, men kan approximeras till inom en faktor två i polynomtid.
• det kinetiska euklidiska minimumspännande trädet kräver en kinetisk datastruktur som kan bibehålla det minsta spännträdet eftersom dess punkter genomgår både kontinuerliga rörelser och insättningar och borttagningar. Flera artiklar har studerat sådana strukturer, och en kinetisk struktur för att algebraiskt förflytta punkter med nästan kubisk total tid, som nästan matchar gränsen för antalet byten, är känd.

Nedre gräns

En asymptotisk nedre gräns för $\Omega (n\log n)$ för det euklidiska minimumspännande trädproblemet kan fastställas i begränsade beräkningsmodeller. Dessa inkluderar det algebraiska beslutsträdet och algebraiska beräkningsträdmodellerna, där algoritmen har tillgång till ingångspunkterna endast genom vissa begränsade primitiver som utför enkla algebraiska beräkningar på sina koordinater. I dessa modeller kräver det närmaste poängparet $\Omega (n\log n)$ tid, men det närmaste paret är nödvändigtvis en kant av det minsta spännträdet, så den minsta spännvidden träd kräver också så mycket tid. Därför är algoritmer för att konstruera det plana minimumspännande trädet i tiden $O(n\log n)$ inom denna modell, till exempel genom att använda Delaunay-trianguleringen, optimala. Dessa nedre gränser gäller dock inte för beräkningsmodeller med heltalspunktkoordinater, där bitvisa operationer och tabellindexeringsoperationer på dessa koordinater är tillåtna. I dessa modeller är snabbare algoritmer möjliga, som beskrivits ovan.

Ansökningar

En uppenbar tillämpning av euklidiska minimumspännande träd är att hitta det billigaste nätverket av ledningar eller rör för att ansluta en uppsättning platser, förutsatt att länkarna kostar ett fast belopp per längdenhet. De första publikationerna om minimumspännande träd gällde mer allmänt en geografisk version av problemet, som involverade designen av ett elnät för södra Mähren, och en tillämpning för att minimera trådlängder i kretsar beskrevs 1957 av Loberman och Weinberger.

Minsta spännande träd är nära besläktade med klustring med enkel länk, en av flera metoder för hierarkisk klustring . Kanterna på ett minsta spännträd, sorterade efter deras längd, ger den ordning i vilken kluster ska slås samman till större kluster i denna klustringsmetod. När väl dessa kanter har hittats, med vilken algoritm som helst, kan de användas för att konstruera enkellänksklustringen i tiden $O(n\log n)$ . Även om de långa tunna klusterformerna som produceras av enkellänkningskluster kan vara en dålig passform för vissa typer av data, såsom blandningar av Gauss-fördelningar , kan det vara ett bra val i applikationer där klustren själva förväntas ha långa tunna former, som vid modellering av galaxernas mörka materia- glorier . Inom geografisk informationsvetenskap har flera forskargrupper använt minsta spännande träd i byggnadernas tyngdpunkter för att identifiera meningsfulla kluster av byggnader, till exempel genom att ta bort kanter som på något annat sätt identifierats som inkonsekventa.

Minimalt spännande träd har också använts för att sluta sig till formen på kurvorna i planet, givet punkter som provats längs kurvan. För en jämn kurva, mer finprovad än dess lokala särdragsstorlek , kommer det minsta spännträdet att bilda en bana som förbinder på varandra följande punkter längs kurvan. Mer generellt kan liknande metoder känna igen kurvor ritade i en prickad eller streckad stil snarare än som en enda ansluten uppsättning. Tillämpningar av denna kurvsökningsteknik inkluderar partikelfysik , för att automatiskt identifiera spåren som partiklar lämnar i en bubbelkammare . Mer sofistikerade versioner av den här idén kan hitta kurvor från ett moln av bullriga provpunkter som ungefär följer kurvkonturen, genom att använda topologin för det spännande trädet för att styra en metod för att röra minsta kvadrater .

En annan tillämpning av minimumspännande träd är en approximationsalgoritm med konstant faktor för det euklidiska resandeförsäljarproblemet , problemet med att hitta den kortaste polygonaliseringen av en punktuppsättning. Att gå runt gränsen för det minsta spännträdet kan uppskatta den optimala resande försäljarturen inom en faktor två av den optimala längden. Emellertid är mer exakta polynom-tidsapproximationsscheman kända för detta problem. I trådlösa ad hoc-nätverk kan sändning av meddelanden längs banor i ett minimumspännande träd vara en exakt uppskattning av sändningsruttningen med minimal energi, vilket återigen är svårt att beräkna exakt .

Insikt

Realiseringsproblemet för euklidiska minimumspännande träd tar ett abstrakt träd som indata och söker en geometrisk plats för varje vertex av trädet (i ett utrymme med någon fast dimension), så att det givna trädet är lika med det minsta spännträdet för dessa punkter . Inte varje abstrakt träd har en sådan insikt; till exempel måste trädet lyda kyssnumret som är förbundet med graden av varje vertex. Ytterligare restriktioner finns; till exempel är det inte möjligt för ett plant minimumspännande träd att ha en grad-sex vertex intill en vertex av grad fem eller sex. Att avgöra om en tvådimensionell realisering existerar är NP-svårt . Beviset för hårdhet beror dock på det faktum att sexgradiga hörn i ett träd har en mycket begränsad uppsättning realiseringar: grannarna till en sådan vertex måste placeras på hörnen av en regelbunden sexhörning centrerad vid den vertexen . För träd med maximal grad fem finns det alltid en plan realisering. På samma sätt, för träd av maximal grad tio, existerar alltid en tredimensionell realisering. För dessa realiseringar kan vissa träd kräva kanter med exponentiell längd och begränsningsrutor med exponentiell yta i förhållande till längden på deras kortaste kant. Träd av maximal grad fyra har mindre plana realiseringar, med polynomiellt avgränsade kantlängder och avgränsande rutor.

Se även

• Rättlinjigt minimumspännande träd , ett minimumspännande träd med avstånd uppmätta med taxigeometri

externa länkar

• EMST handledning , mlpack dokumentation