Ekvivalent potentiell temperatur

Ekvivalent potentiell temperatur , vanligen kallad theta-e $\left(\theta _{e}\right)$ , är en kvantitet som bevaras under ändringar av ett luftpakets tryck (det vill säga under vertikala rörelser i atmosfären ), även om vattenånga kondenserar under tryckförändringen. Den är därför mer bevarad än den vanliga potentiella temperaturen , som förblir konstant endast för omättade vertikala rörelser (tryckförändringar).

$\theta _{e}$ är den temperatur ett luftpaket skulle nå om all vattenånga i paketet skulle kondensera och frigöra sin latenta värme och paketet bringades adiabatiskt till ett standardreferenstryck, vanligtvis 1000 hPa (1000 mbar ) vilket är ungefär lika med atmosfärstrycket vid havsnivån .

Dess användning för att uppskatta atmosfärisk stabilitet

Stabilitet av inkompressibel vätska

Liksom en boll som är balanserad på toppen av en kulle, skulle tätare vätska som ligger ovanför mindre tät vätska vara dynamiskt instabil: vältande rörelser ( konvektion ) kan sänka tyngdpunkten och kommer således att inträffa spontant, vilket snabbt producerar en stabil skiktning som alltså är den observerade skick nästan hela tiden. Förutsättningen för stabilitet hos en inkompressibel vätska är att densiteten minskar monotont med höjden .

Kompressibel lufts stabilitet: potentiell temperatur

Om en vätska är komprimerbar som luft, innebär kriteriet för dynamisk stabilitet istället potentialdensitet , vätskans densitet vid ett fast referenstryck. För en idealgas (se gaslagar ) är stabilitetskriteriet för en luftpelare att potentiell temperatur ökar monotont med höjden .

För att förstå detta, överväg torr konvektion i atmosfären, där den vertikala variationen i tryck är betydande och adiabatisk temperaturförändring är viktig: När ett luftpaket rör sig uppåt sjunker det omgivande trycket, vilket får paketet att expandera. En del av inre energi går åt till det arbete som krävs för att expandera mot atmosfärstrycket, så paketets temperatur sjunker trots att det inte har tappat någon värme. Omvänt komprimeras ett sjunkande paket och blir varmare trots att ingen värme tillförs.

Luften på toppen av ett berg är vanligtvis kallare än luften i dalen nedanför, men arrangemanget är inte instabilt: om ett luftpaket från dalen på något sätt lyftes upp till toppen av berget, när det anlände skulle det vara ännu kallare än luften som redan finns där, på grund av adiabatisk kylning; den skulle vara tyngre än den omgivande luften och skulle sjunka tillbaka mot sin ursprungliga position. På samma sätt, om ett paket kall luft från bergstoppen skulle ta sig ner till dalen, skulle den komma varmare och lättare än dalluften och flyta tillbaka upp på berget.

Så kall luft som ligger ovanpå varm luft kan vara stabil, så länge som temperaturminskningen med höjden är mindre än den adiabatiska förfallohastigheten ; den dynamiskt viktiga storheten är inte temperaturen, utan den potentiella temperaturen - den temperatur luften skulle ha om den fördes adiabatiskt till ett referenstryck. Luften runt berget är stabil eftersom luften på toppen, på grund av sitt lägre tryck, har en högre potentiell temperatur än den varmare luften under.

Effekter av vattenkondensering: ekvivalent potentiell temperatur

Ett stigande luftpaket som innehåller vattenånga, om det stiger tillräckligt långt, når sin höjda kondensnivå : det blir mättat med vattenånga (se förhållandet mellan Clausius och Clapeyron) . Om luftpaketet fortsätter att stiga, kondenserar vattenånga och avger sin latenta värme till den omgivande luften, vilket delvis motverkar den adiabatiska kylningen. En mättad luftpaket kyler därför mindre än en torr luft skulle när den stiger (dess temperatur ändras med höjden vid den fuktiga adiabatiska förfallningshastigheten, som är mindre än den torra adiabatiska förfallningshastigheten ). Ett sådant mättat luftpaket kan uppnå flytkraft , och därmed accelerera ytterligare uppåt, ett skenande tillstånd (instabilitet) även om den potentiella temperaturen ökar med höjden. Det tillräckliga villkoret för att en luftpelare ska vara absolut stabil, även med avseende på mättade konvektiva rörelser, är att den ekvivalenta potentiella temperaturen måste öka monotont med höjden.

Formel

Definitionen av den ekvivalenta potentialtemperaturen är:

$\theta _{e}=T\left({\frac {p_{0}}{p}}\right)^{R_{d}/(c_{pd}+r_{t }c)}H^{-r_{v}R_{v}/(c_{pd}+r_{t}c)}\exp \left[{\frac {L_{v}r_{v}}{( c_{pd}+r_{t}c)T}}\right]$

Var:

• $T$ är temperaturen [K] för luft vid tryck $p$ ,
• $p_{0}$ är ett referenstryck som tas som 1000 hPa,
• $p$ är trycket vid punkten,
• $R_{d}$ och $R_{v}$ är de specifika gaskonstanterna för torr luft respektive vattenånga,
• $c_{pd}$ och $c$ är de specifika värmekapaciteterna hos torr luft respektive flytande vatten,
• $r_{t}$ och ${\displaystyle r_{v}} är de totala$ blandningsförhållandena för vatten respektive vattenånga ,
• $H$ är den relativa luftfuktigheten ,
• $L_{v}$ är vattnets latenta förångningsvärme .

Ett antal ungefärliga formuleringar används för att beräkna ekvivalent potentiell temperatur, eftersom det inte är lätt att beräkna integrationer längs paketets rörelse. Bolton (1980) ger en genomgång av sådana procedurer med uppskattningar av fel. Hans bästa approximationsformel används när noggrannhet behövs:

$\theta _{e}=\theta _{L}\exp \left[\left({\frac {3036}{T_{L}}}-1.78\right)r\left(1+0.448r\right)\right]$

${ \displaystyle \theta _{L}=T\left({\frac {p_{0}}{pe}}\right)^{\kappa _{d}}\left({\frac {T}{T_{ L}}}\right)^{0.28r}}$

$T_{L}={\frac {1}{ {\frac {1}{T_{d}-56}}+{\frac {\log _{e}(T/T_{d})}{800}}}}+56$

Var:

• $\theta _{L}$ är (torr) potentiell temperatur [K] vid den höjda kondensationsnivån (LCL),
• $T_{L}$ är (ungefärlig) temperatur [K] vid LCL,
• $T_{d}$ är daggpunktstemperatur vid tryck $p$ ,
• $e$ är vattenångtrycket (för att erhålla $\theta _{L}$ för torr luft),
• $\kappa _{d}=R_{d}/c_{pd}$ är förhållandet mellan den specifika gaskonstanten och den specifika värmen hos torr luft vid konstant tryck (0,2854) ,
• $r$ är blandningsförhållandet mellan vattenångmassan per massa [kg/kg] (ibland anges värdet i [g/kg] och det bör delas med 1000).

En lite mer teoretisk formel används ofta i litteratur som Holton (1972) när teoretisk förklaring är viktig:

$\theta _{e}\approx \theta _{L}\exp \left[{\ frac {r_{s}(T_{L})L_{v}(T_{L})}{c_{pd}T_{L}}}\höger]$

Var:

• $r_{s}(T_{L})$ är mättat blandningsförhållande för vatten vid temperatur $T_{L}$ , temperaturen vid luftens mättnadsnivå,
• $L_{v}(T_{L})$ är latent förångningsvärme vid temperatur $T_{L}$ (2406 kJ/kg {vid 40 °C} till kJ/kg {vid 0 °C}), och
• $c_{pd}$ är specifik värme av torr luft vid konstant tryck (1005,7 J/(kg·K)).

Ytterligare mer förenklad formel används (i till exempel Stull 1988 §13.1 s. 546) för enkelhetens skull, om det är önskvärt att undvika att beräkna $T_{L}$ :

$\theta _{e}=T_{e}\left({\ frac {p_{0}}{p}}\right)^{\kappa _{d}}\approx \left(T+{\frac {L_{v}}{c_{pd}}}r\right)\ vänster({\frac {p_{0}}{p}}\right)^{\frac {R_{d}}{c_{pd}}}$

Var:

• $T_{e}$ = ekvivalent temperatur
• $R_{d}$ = specifik gaskonstant för luft (287,04 J/(kg·K))

Användande

Tillbaka banor av luftmassor mellan 31 december 1997 och januari 1998 som orsakade den nordamerikanska isstormen 1998

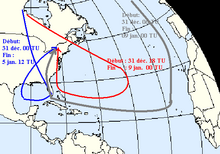
Detta gäller på den synoptiska skalan för karakterisering av luftmassor. Till exempel, i en studie av den nordamerikanska isstormen 1998, har professorerna Gyakum ( McGill University , Montreal ) och Roebber ( University of Wisconsin-Milwaukee ) visat att de inblandade luftmassorna härstammar från högarktis på en höjd av 300 till 400 hPa föregående vecka, gick ner mot ytan när de flyttade till tropikerna och flyttade sedan tillbaka upp längs Mississippidalen mot St. Lawrencedalen . Bakåtbanorna utvärderades med användning av konstanta ekvivalenta potentiella temperaturer.

I mesoskalan är ekvivalent potentiell temperatur också ett användbart mått på den omättade atmosfärens statiska stabilitet. Under normala, stabilt skiktade förhållanden ökar den potentiella temperaturen med höjden,

${\frac {\partial \theta _{e}}{\partial z}}>0$

och vertikala rörelser undertrycks. Om den ekvivalenta potentiella temperaturen minskar med höjden,

${\frac {\partial \theta _{e}}{\partial z}}<0$

atmosfären är instabil för vertikala rörelser, och konvektion är trolig. Situationer där den ekvivalenta potentiella temperaturen minskar med höjden, vilket indikerar instabilitet i mättad luft, är ganska vanliga.

Se även

• Meteorologi
• Fuktig statisk energi
• Potentiell temperatur
• Väderprognos

Bibliografi

•     MK Yau och RR Rogers, Short Course in Cloud Physics, tredje upplagan , publicerad av Butterworth-Heinemann, 1 januari 1989, 304 sidor. ISBN 9780750632157 ISBN 0-7506-3215-1