Dynamisk mekanisk analys

Dynamisk mekanisk analys

Akronym	DMA
Klassificering	Termisk analys
Andra tekniker
Relaterad	Isotermisk titreringskalorimetri Dynamisk mekanisk analys Termomekanisk analys Termogravimetrisk analys Differentiell termisk analys Dielektrisk termisk analys

Dynamisk mekanisk analys (förkortat DMA ) är en teknik som används för att studera och karakterisera material. Det är mest användbart för att studera det viskoelastiska beteendet hos polymerer . En sinusformad spänning appliceras och töjningen i materialet mäts, vilket gör att man kan bestämma komplexmodulen. Provets temperatur eller spänningens frekvens varieras ofta, vilket leder till variationer i komplexmodulen; detta tillvägagångssätt kan användas för att lokalisera glasövergångstemperaturen för materialet, såväl som för att identifiera övergångar som motsvarar andra molekylära rörelser.

Teori

Viskoelastiska egenskaper hos material

Figur 1. En typisk DMA-testare med grepp för att hålla provet och miljökammare för att ge olika temperaturförhållanden. Ett prov är monterat på greppen och miljökammaren kan glida över för att omsluta provet.

Polymerer som består av långa molekylkedjor har unika viskoelastiska egenskaper, som kombinerar egenskaperna hos elastiska fasta ämnen och newtonska vätskor . Den klassiska teorin om elasticitet beskriver de mekaniska egenskaperna hos elastiskt fast material där spänningen är proportionell mot töjningen vid små deformationer. Sådana reaktioner på stress är oberoende av töjningshastigheten . Den klassiska teorin om hydrodynamik beskriver egenskaperna hos viskös vätska, för vilken spänningsresponsen är beroende av töjningshastigheten. Detta fasta och vätskeliknande beteende hos polymerer kan modelleras mekaniskt med kombinationer av fjädrar och instrumentbrädor.

Dynamiska moduler av polymerer

Den viskoelastiska egenskapen hos en polymer studeras genom dynamisk mekanisk analys där en sinusformad kraft (spänning σ) appliceras på ett material och den resulterande förskjutningen (töjningen) mäts. För en perfekt elastisk fast substans kommer den resulterande töjningen och spänningen att vara perfekt i fas. För en rent viskös vätska kommer det att finnas en 90 graders fasfördröjning med avseende på spänning. Viskoelastiska polymerer har egenskaperna däremellan där viss fasfördröjning kommer att inträffa under DMA-tester. När spänningen appliceras och spänningen släpar efter, gäller följande ekvationer:

• Stress: $\sigma =\sigma _{0}\sin(t\omega +\delta )\,$
• Stam: $\varepsilon =\varepsilon _{0}\sin(t\omega )$

var

$\omega$ är frekvensen av töjningsoscillation,

$t$ är tid,

$\delta$ är fasförskjutning mellan spänning och töjning.

Betrakta det rent elastiska fallet, där spänningen är proportionell mot töjningen som ges av Youngs modul $E$ . Vi har $\sigma (t)=E\epsilon (t)\implies \ sigma _{0}\sin {(\omega t+\delta )}=E\epsilon _{0}\sin {\omega t}\implies \delta =0$

Nu för det rent viskösa fallet, där spänningen är proportionell mot töjningshastigheten . $\sigma (t)=K{\frac {d\epsilon }{dt}}\implies \sigma _{0}\sin {(\omega t+\delta )}=K\epsilon _{0}\omega \cos {\omega t}\implies \delta ={\frac { \pi }{2}}$

Lagringsmodulen mäter den lagrade energin, som representerar den elastiska delen, och förlustmodulen mäter energin som avges som värme, representerande den viskösa delen. Draghållnings- och förlustmodulerna definieras enligt följande:

• Lagringsmodul: $E'={\frac {\sigma _{0}}{\varepsilon _{0}}}\cos \delta$
• Förlustmodul: $E''={\frac {\sigma _{0}}{\varepsilon _{0}}}\sin \delta$
• Fasvinkel: $\delta =\arctan {\frac {E''}{E'}}$

På liknande sätt, i skjuvningsfallet istället för spänningsfallet, definierar vi också skjuvlagrings- och förlustmoduler, $G'$ och $G''$ .

Komplexa variabler kan användas för att uttrycka modulerna $E^{*}$ och $G^{*}$ enligt följande:

$E^{*}=E'+iE''={\frac {\sigma _{0}}{\varepsilon _{0}} }e^{i\delta }\,$

$G^{*}=G'+iG''\,$

var

${i}^{2}=-1\,$

Härledning av dynamiska moduler

Skjuvspänning $\sigma (t)=\int _{-\infty }^{t}G( tt'){\dot {\gamma }}(t')dt'$ av ett finit element i en riktning kan uttryckas med relaxationsmodul $G(tt')$ och töjningshastighet , integrerad över alla tidigare tider $t'$ upp till den aktuella tiden $t$ . Med töjningshastighet ${\dot {\gamma (t)}}=\omega \cdot \gamma _{0}\cdot \cos(\ omega t)$ och substitution $\xi (t')=tt'=s$ man får $\sigma (t)=\int _{\xi (-\infty )=t-(-\infty )}^{\xi (t)=tt}G(s)\omega \ gamma _{0}\cdot \cos(\omega (ts))(-ds)=\gamma _{0}\int _{0}^{\infty }\omega G(s)\cos(\omega ( ts))ds$ . Tillämpning av trigonometrisk additionssats $\cos(x\pm y)=\cos( x)\cos(y)\mp \sin(x)\sin(y)$ leder till uttrycket

${\frac {\sigma (t)}{\gamma (t)}}=\underbrace {[\omega \int _{o}^{\infty }G(s)\sin(\omega s) ds]} _{{\text{skjuvlagringsmodul }}G'}\sin(\omega t)+\underbrace {[\omega \int _{o}^{\infty }G(s)\cos(\ omega s)ds]} _{{\text{skjuvförlustmodul }}G''}\cos(\omega t).\,$

med konvergerande integraler, om $G(s)\rightarrow 0$ för $s\rightarrow \infty$ , som beror på frekvens men inte på tid. Förlängning av $\sigma (t)=\sigma _{0}\cdot \sin(\omega \cdot t+\Delta \varphi )$ med trigonometrisk identitet $\sin(x\pm y)=\sin(x )\cdot \cos(y)\pm \cos(x)\cdot \sin(y)$ leder till

${\frac {\sigma (t)}{\gamma (t)}}=\underbrace {{\frac {\sigma _{0}}{\gamma _{0}}}\cdot \cos( \Delta \varphi )} _{G'}\cdot \sin(\omega \cdot t)+\underbrace {{\frac {\sigma _{0}}{\gamma _{0}}}\cdot \sin (\Delta \varphi )} _{G''}\cdot \cos(\omega \cdot t)\,$ .

Jämförelse av de två ${\frac {\sigma (t)}{\gamma (t)}}$ ekvationerna leder till definitionen av $G'$ och $G''$ .

Ansökningar

Mätning av glasets övergångstemperatur

En viktig tillämpning av DMA är mätning av glasövergångstemperaturen för polymerer. Amorfa polymerer har olika glasövergångstemperaturer, över vilka materialet kommer att ha gummiliknande egenskaper istället för glasaktigt beteende och materialets styvhet kommer att minska dramatiskt tillsammans med en minskning av dess viskositet. Vid glasövergången minskar lagringsmodulen dramatiskt och förlustmodulen når ett maximum. Temperatursvepande DMA används ofta för att karakterisera glasövergångstemperaturen för ett material.

Figur 2. Typiskt DMA-termogram av en amorf termoplast (polykarbonat). Lagringsmodul (E') och förlustmodul (E'') och förlustfaktor tan(delta) plottas som funktion av temperaturen. Glasövergångstemperaturen för polykarbonat detekterades vara runt 151°C (utvärdering enligt ISO 6721-11)

Polymersammansättning

₀₀ Att variera sammansättningen av monomerer och tvärbindning kan lägga till eller ändra funktionaliteten hos en polymer som kan förändra resultaten från DMA. Ett exempel på sådana förändringar kan ses genom att blanda etylenpropylendienmonomer (EPDM) med styren-butadiengummi (SBR) och olika tvärbindnings- eller härdningssystem. Nair et al. förkorta blandningar som E S, E ₂₀ S, etc., där E S är lika med viktprocenten EPDM i blandningen och S betecknar svavel som härdare.

En ökning av mängden SBR i blandningen minskade lagringsmodulen på grund av intermolekylära och intramolekylära interaktioner som kan förändra det fysiska tillståndet hos polymeren. Inom den glasartade regionen visar EPDM den högsta lagringsmodulen på grund av starkare intermolekylära interaktioner (SBR har mer steriskt hinder som gör det mindre kristallint). I det gummiartade området visar SBR den högsta lagringsmodulen som är resultatet av dess förmåga att motstå intermolekylär glidning.

Jämfört med svavel inträffade den högre lagringsmodulen för blandningar härdade med dikumylperoxid (DCP) på grund av den relativa styrkan hos CC- och CS-bindningar.

Införlivande av förstärkande fyllmedel i polymerblandningarna ökar också lagringsmodulen på bekostnad av att begränsa förlusttangentets topphöjd.

DMA kan också användas för att effektivt utvärdera blandbarheten av polymerer. E ₄₀ S-blandningen hade en mycket bredare övergång med en skuldra istället för ett brant fall i ett lagringsmoduldiagram med varierande blandningsförhållanden, vilket indikerar att det finns områden som inte är homogena.

Instrumentation

Figur 3. Allmänt schema över ett DMA-instrument.

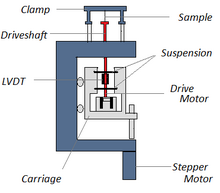
Instrumenteringen av en DMA består av en förskjutningssensor såsom en linjär variabel differentialtransformator , som mäter en förändring i spänningen som ett resultat av att instrumentsonden rör sig genom en magnetisk kärna, ett temperaturkontrollsystem eller en ugn, en drivmotor (en linjär motor för sondbelastning som ger belastning för den applicerade kraften), ett drivaxelstöd och styrsystem för att fungera som en styrning för kraften från motorn till provet, och provklämmor för att hålla provet som testas. Beroende på vad som mäts kommer prover att förberedas och hanteras på olika sätt. Ett allmänt schema över de primära komponenterna i ett DMA-instrument visas i figur 3.

Typer av analysatorer

Det finns två huvudtyper av DMA-analysatorer som används för närvarande: tvångsresonansanalysatorer och friresonansanalysatorer. Friresonansanalysatorer mäter de fria svängningarna av dämpningen av provet som testas genom att suspendera och svänga provet. En begränsning till friresonansanalysatorer är att den är begränsad till stavformade eller rektangulära prover, men prover som kan vävas/flätas är också tillämpliga. Tvångsresonansanalysatorer är den vanligaste typen av analysatorer som finns i instrumentering idag. Dessa typer av analysatorer tvingar provet att oscillera med en viss frekvens och är tillförlitliga för att utföra ett temperatursvep.

Figur 4. Vridningsrörelser kontra axiella rörelser.

Analysatorer är gjorda för kontroll av både spänning (kraft) och töjning (förskjutning). Vid töjningskontroll förskjuts sonden och den resulterande spänningen hos provet mäts genom att implementera en kraftbalansomvandlare, som använder olika axlar. Fördelarna med töjningskontroll inkluderar en bättre korttidsrespons för material med låg viskositet och experiment med spänningsavslappning görs relativt lätt. Vid stresskontroll appliceras en inställd kraft på provet och flera andra experimentella förhållanden (temperatur, frekvens eller tid) kan varieras. Stresskontroll är vanligtvis billigare än töjningskontroll eftersom endast ett skaft behövs, men detta gör det också svårare att använda. Några fördelar med stresskontroll inkluderar det faktum att strukturen i provet är mindre sannolikt att förstöras och längre avslappningstider/längre krypstudier kan göras mycket lättare. Karakteristiska lågviskösa material har en nackdel av korttidssvar som begränsas av tröghet . Spännings- och töjningskontrollanalysatorer ger ungefär samma resultat så länge karakteriseringen är inom det linjära området för polymeren i fråga. Spänningskontroll ger dock ett mer realistiskt svar eftersom polymerer har en tendens att motstå en belastning.

Spänning och töjning kan appliceras via vrid- eller axialanalysatorer. Torsionsanalysatorer används huvudsakligen för vätskor eller smältor men kan även implementeras för vissa fasta prover eftersom kraften appliceras i en vridande rörelse. Instrumentet kan göra experiment med kryp-återhämtning, stress-avslappning och stress-belastning. Axiella analysatorer används för fasta eller halvfasta material. Den kan göra böjnings-, drag- och kompressionstestning (även skjuv- och vätskeprover om så önskas). Dessa analysatorer kan testa material med högre modul än torsionsanalysatorer. Instrumentet kan göra av termomekanisk analys (TMA) utöver de experiment som torsionsanalysatorer kan göra. Figur 4 visar den allmänna skillnaden mellan de två tillämpningarna av spänning och töjning.

Ändring av provgeometri och fixturer kan göra spännings- och töjningsanalysatorer praktiskt taget likgiltiga för varandra utom i de yttersta ändarna av provfaserna, dvs riktigt flytande eller stela material. Vanliga geometrier och fixturer för axialanalysatorer inkluderar trepunkts- och fyrapunktsböjning, dubbel- och enkelutbärande, parallella plattor och varianter, bulk-, förlängnings-/drag- och skjuvplattor och sandwiches. Geometrier och fixturer för torsionsanalysatorer består av parallella plattor, kon-och-platta, couette och torsionsbalk och fläta. För att kunna använda DMA för att karakterisera material måste det faktum att små dimensionsförändringar också kan leda till stora felaktigheter i vissa tester åtgärdas. Tröghet och skjuvuppvärmning kan påverka resultaten av antingen forcerade eller fria resonansanalysatorer, särskilt i vätskeprover.

Testlägen

Två huvudtyper av testlägen kan användas för att undersöka de viskoelastiska egenskaperna hos polymerer: temperatursvep- och frekvenssveptest. Ett tredje, mindre vanligt studerat testläge är dynamisk belastningstestning.

Temperatursvep

En vanlig testmetod innebär att man mäter den komplexa modulen vid låg konstant frekvens samtidigt som provets temperatur varieras. En framträdande topp i $\tan(\delta )$ uppträder vid glasövergångstemperaturen för polymeren. Sekundära övergångar kan också observeras, vilket kan tillskrivas den temperaturberoende aktiveringen av en mängd olika kedjerörelser. I semikristallina polymerer kan separata övergångar observeras för de kristallina och amorfa sektionerna. På liknande sätt finns ofta flera övergångar i polymerblandningar.

Blandningar av polykarbonat och poly( akrylnitril-butadien-styren ) studerades till exempel med avsikten att utveckla ett polykarbonatbaserat material utan polykarbonats tendens till spröda brott . Temperatursvepande DMA av blandningarna visade två starka övergångar som sammanfaller med glasövergångstemperaturerna för PC och PABS, i överensstämmelse med upptäckten att de två polymererna var oblandbara.

Frekvenssvep

Figur 5. Ett frekvenssveptest på polykarbonat under rumstemperatur (25 °C). Lagringsmodul (E') och förlustmodul (E'') plottades mot frekvens. Ökningen av frekvensen "fryser" kedjerörelserna och ett styvare beteende observerades.

Ett prov kan hållas vid en fast temperatur och kan testas med varierande frekvens. Toppar i $\tan(\delta )$ och i E'' med avseende på frekvens kan associeras med glasövergången, vilket motsvarar kedjornas förmåga att röra sig förbi varandra. Observera att detta innebär att glasövergången är beroende av töjningshastighet utöver temperaturen. Sekundära övergångar kan också observeras.

Maxwell -modellen ger en bekväm, om inte strikt exakt, beskrivning av viskoelastiska material. Att applicera en sinusformad spänning på en Maxwell-modell ger: $E''={\frac {E\tau _{0}\omega }{\tau _{0 }^{2}\omega ^{2}+1}},$ där $\tau _{0}=\eta /E$ är Maxwell-relaxationstiden. Således observeras en topp i E'' vid frekvensen $1/\tau _{0}$ . En riktig polymer kan ha flera olika relaxationstider förknippade med olika molekylära rörelser.

Dynamiska stress-belastningsstudier

Genom att gradvis öka svängningarnas amplitud kan man utföra en dynamisk spännings-töjningsmätning. Variationen av lagrings- och förlustmoduler med ökande spänning kan användas för materialkaraktärisering och för att bestämma den övre gränsen för materialets linjära spännings-töjningsregim.

Kombinerat svep

Eftersom glasövergångar och sekundära övergångar ses i både frekvensstudier och temperaturstudier finns det intresse för multidimensionella studier, där temperatursvep utförs vid en mängd olika frekvenser eller frekvenssvep utförs vid en mängd olika temperaturer. Denna typ av studie ger en rik karakterisering av materialet och kan ge information om arten av den molekylära rörelse som är ansvarig för övergången.

Till exempel har studier av polystyren (Tg _≈110 °C) noterat en sekundär övergång nära rumstemperatur. Temperatur-frekvensstudier visade att övergångstemperaturen till stor del är frekvensoberoende, vilket tyder på att denna övergång är resultatet av en rörelse av ett litet antal atomer; det har föreslagits att detta är resultatet av rotationen av fenylgruppen runt huvudkedjan.

Se även

• Maxwell material
• Standard linjärt massivt material
• Termomekanisk analys
• Dielektrisk termisk analys
• Tid–temperatur överlagring
• Elektroaktiva polymerer

externa länkar

• Dynamisk mekanisk analys hämtad 21 maj 2019.