Dynamisk epistemisk logik
Dynamisk epistemisk logik (DEL) är ett logiskt ramverk som handlar om kunskaps- och informationsförändring. Vanligtvis fokuserar DEL på situationer som involverar flera agenter och studerar hur deras kunskap förändras när händelser inträffar. Dessa händelser kan ändra faktiska egenskaper hos den faktiska världen (de kallas ontiska händelser ): till exempel är ett rött kort målat i blått. De kan också åstadkomma förändringar av kunskap utan att förändra världens faktiska egenskaper (de kallas epistemiska händelser ): till exempel avslöjas ett kort offentligt (eller privat) som rött. Ursprungligen fokuserade DEL på epistemiska händelser. Vi presenterar bara i det här inlägget några av grundidéerna i det ursprungliga DEL-ramverket; mer information om DEL i allmänhet finns i referenserna.
På grund av arten av dess studieobjekt och dess abstrakta tillvägagångssätt är DEL relaterad och har tillämpningar till många forskningsområden, såsom datavetenskap ( artificiell intelligens ), filosofi ( formell epistemologi ), ekonomi ( spelteori ) och kognitionsvetenskap . Inom datavetenskap är DEL till exempel mycket relaterat till multi-agent system , som är system där flera intelligenta agenter interagerar och utbyter information.
Som en kombination av dynamisk logik och epistemisk logik är dynamisk epistemisk logik ett ungt forskningsfält. Det började egentligen 1989 med Plazas logik med offentligt tillkännagivande. Oberoende av varandra föreslog Gerbrandy och Groeneveld ett system som dessutom behandlade privat tillkännagivande och som var inspirerat av Veltmans arbete. Ett annat system föreslogs av van Ditmarsch vars främsta inspiration var Cluedo -spelet. Men det mest inflytelserika och originella systemet var systemet som föreslogs av Baltag, Moss och Solecki. Detta system kan hantera alla typer av situationer som studerats i verken ovan och dess underliggande metodik är konceptuellt grundad. Vi kommer att presentera några av dess grundläggande idéer i det här inlägget.
Formellt utökar DEL vanlig epistemisk logik genom att inkludera händelsemodeller för att beskriva åtgärder, och en produktuppdateringsoperatör som definierar hur epistemiska modeller uppdateras som en konsekvens av att utföra åtgärder som beskrivs genom händelsemodeller. Epistemisk logik kommer först att återkallas. Sedan kommer åtgärder och händelser in i bilden och vi kommer att introducera DEL-ramverket.
Epistemisk logik
Epistemisk logik är en modal logik som handlar om begreppen kunskap och tro. Som en logik handlar det om att förstå processen för resonemang om kunskap och tro: vilka principer som relaterar till begreppen kunskap och tro är intuitivt rimliga? Liksom epistemologi härrör det från det grekiska ordet eller 'episteme' som betyder kunskap. Epistemologi är ändå mer angelägen om att analysera själva naturen och omfattningen av kunskap och ta upp frågor som "Vad är definitionen av kunskap?" eller "Hur förvärvas kunskap?". Faktum är att epistemisk logik växte fram ur epistemologin under medeltiden tack vare ansträngningarna från Burley och Ockham. Det formella arbete, baserat på modal logik, som invigde samtida forskning om epistemisk logik går tillbaka endast till 1962 och beror på Hintikka . Det väckte sedan på 1960-talet diskussioner om principerna för kunskap och tro och många axiom för dessa föreställningar föreslogs och diskuterades. Till exempel anses interaktionsaxiomen och ofta vara intuitiva principer: om en agent vet då (s)han tror också , eller om en agent tror , då (s)han vet att (s)han tror . På senare tid har den här typen av filosofiska teorier tagits upp av forskare inom ekonomi , artificiell intelligens och teoretisk datavetenskap där resonemang om kunskap är ett centralt ämne. På grund av den nya miljön där epistemisk logik användes, lades nya perspektiv och nya funktioner som beräkningsbarhetsfrågor till på forskningsagendan för epistemisk logik.
Syntax
I uppföljaren är en finit mängd vars element kallas agenter och är en uppsättning satsbokstäver.
Det epistemiska språket är en förlängning av det grundläggande multimodala språket för modal logik med en gemensam kunskapsoperator och en distribuerad kunskapsoperator D . Formellt definieras det epistemiska språket induktivt av följande grammatik i BNF :
där , och . Det grundläggande epistemiska språket är språket utan allmän kunskap och distribuerade kunskapsoperatörer. Formeln är en förkortning för (för ett givet , är en förkortning för , är en förkortning för och en förkortning för .
Gruppbegrepp: allmän, gemensam och distribuerad kunskap.
I en miljö med flera agenter finns det tre viktiga epistemiska begrepp: allmän kunskap, distribuerad kunskap och allmän kunskap. Begreppet allmän kunskap studerades först av Lewis i samband med konventioner. Det applicerades sedan på distribuerade system och på spelteori , där det gör det möjligt att uttrycka att spelarnas rationalitet, spelreglerna och spelaruppsättningen är allmänt kända.
Allmänbildning.
Allmän kunskap om betyder att alla i gruppen av agenter vet att . Formellt motsvarar detta följande formel:
Allmänbildning.
Allmän kunskap om betyder att alla känner till men också att alla vet att alla vet , att alla vet att alla vet att alla vet , och så vidare i det oändliga . Formellt motsvarar detta följande formel
Eftersom vi inte tillåter oändlig konjunktion måste begreppet allmän kunskap introduceras som en primitiv i vårt språk.
Innan vi definierar språket med denna nya operator, kommer vi att ge ett exempel introducerat av Lewis som illustrerar skillnaden mellan begreppen allmän kunskap och allmän kunskap. Lewis ville veta vilken typ av kunskap som behövs så att påståendet : "alla förare måste köra till höger" blir en konvention bland en grupp agenter. Med andra ord ville han veta vilken typ av kunskap som behövs för att alla ska känna sig trygga att köra till höger. Anta att det bara finns två agenter och . Då räcker inte alla som känner till (formellt Det kan faktiskt fortfarande vara möjligt att agenten anser att agenten inte känner till (formellt ). I så fall kommer agenten inte att känna sig säker att köra till höger eftersom han kanske anser att agenten utan att veta , skulle kunna köra till vänster. För att undvika detta problem skulle vi då kunna anta att alla vet att alla vet att (formellt . Detta är återigen inte tillräckligt för att säkerställa att alla känner sig säkra att köra till höger. Det kan faktiskt fortfarande vara möjligt att agent anser möjligt att agent anser vara möjligt att agent inte känner till (formellt ). I så fall och från s synvinkel, anser utan att veta , kommer att köra till vänster. Så från s synvinkel kan också köra till vänster (med samma argument som ovan). Så kommer inte att känna sig säker att köra till höger. Med induktionsresonemang visade Lewis att för alla , räcker inte för att förarna ska känna sig trygga att köra till höger. Det vi behöver är faktiskt en oändlig konjunktion. Med andra ord behöver vi allmän kunskap om : .
Distribuerad kunskap.
Distribuerad kunskap om betyder att om agenterna drog ut sin kunskap helt och hållet skulle de veta att gäller. Med andra ord är kunskapen om fördelad mellan agenterna. Formeln lyder som 'det är distribuerad kunskap bland uppsättningen agenter som innehåller'.
Semantik
Epistemisk logik är en modal logik . Så, vad vi kallar en epistemisk modell är bara en Kripke-modell enligt definition i modal logik. Mängden är en icke-tom mängd vars element kallas möjliga världar och tolkningen är en funktion som specificerar vilka propositionella fakta (som "Ann har det röda kortet") som är sanna i var och en av dessa världar. Tillgänglighetsrelationerna är binära relationer för varje agent } ; de är avsedda att fånga osäkerheten hos varje agent (om den faktiska världen och om de andra agenternas osäkerhet). Intuitivt har vi när världen är kompatibel med agent s information i world eller, med andra ord, när agent anser att världen kan motsvara världen (ur denna synvinkel). Vi skriver felaktigt för och betecknar mängden världar .
Intuitivt representerar en spetsig epistemisk modell , där , från en extern synvinkel hur den faktiska världen uppfattas av agenterna .
För varje epistemisk modell , varje och varje , vi definierar induktivt med följande sanningsvillkor :
| iff | ||
| iff | ||
| iff | ||
| iff | ||
| iff | ||
| iff |
där den transitiva stängningen av vi har att om, och endast om, det finns och så att och för alla , .
Trots att begreppet gemensam tro måste introduceras som en primitiv i språket, kan vi notera att definitionen av epistemiska modeller inte behöver modifieras för att ge sanningsvärde åt den gemensamma kunskapen och distribuerade kunskapsoperatörer.
Exempel på kort:
Spelare , och (står för Ann, Bob och Claire) spelar ett kortspel med tre kort: ett rött, ett grönt och ett blått. Var och en av dem har ett enda kort men de känner inte till de andra spelarnas kort. Ann har det röda kortet, Bob har det gröna kortet och Claire har det blåa kortet. Detta exempel är avbildat i den spetsiga epistemiska modellen som representeras nedan. I det här exemplet, och . Varje värld är märkt med satsbokstäverna som är sanna i denna värld och motsvarar den faktiska världen. Det finns en pil indexerad av agent från en möjlig värld till en möjlig värld när . Reflexiva pilar utelämnas, vilket betyder att för alla och alla , vi har att .
står för: " har det röda kortet''
står för: " har det blå kortet''
står för: " har det gröna kortet''
och så vidare...
När tillgänglighetsrelationer är ekvivalensrelationer (som i det här exemplet) och vi har att , säger vi att agent kan inte skilja värld från värld (eller värld går inte att skilja från värld för agent ). Så till exempel inte skilja den faktiska världen från den möjliga världen där har det blå kortet ( ), har det gröna kortet ( ) och har fortfarande det röda kortet ( ).
I synnerhet gäller följande uttalanden:
"Alla agenter vet färgen på sitt kort".
' vet att har antingen det blåa eller det gröna kortet och att har antingen det blåa eller det gröna kortet'.
"Alla vet att har antingen det röda, gröna eller blåa kortet och detta är till och med allmänt känt bland alla agenter".
Kunskap kontra tro
Vi använder samma notation för både kunskap och tro. Därför, beroende på sammanhanget, antingen att läsa 'agenten K nu som gäller' eller 'agenten Tror att gäller'. En avgörande skillnad är att till skillnad från kunskap kan föreställningar vara fel : axiomet gäller bara för kunskap, men inte nödvändigtvis för tro. Detta axiom som kallas axiom T (för sanning) säger att om agenten känner till en proposition så är denna proposition sann. Den anses ofta vara kunskapens kännetecken och den har inte utsatts för någon allvarlig attack ända sedan den introducerades i Theaetetus av Platon .
Begreppet kunskap kan överensstämma med vissa andra begränsningar (eller axiom) såsom om agent vet något, hon vet att hon vet det. Dessa begränsningar kan påverka karaktären på tillgänglighetsrelationerna som sedan kan överensstämma med några extra egenskaper. Så vi kommer nu att definiera några speciella klasser av epistemiska modeller som alla lägger till några extra begränsningar för tillgänglighetsrelationerna . Dessa begränsningar matchas av särskilda axiom för kunskapsoperatorn . Under varje egenskap ger vi axiomet som definierar klassen av epistemiska ramar som uppfyller denna egenskap. ( står för för alla .)
| serie | |
| D | |
| transitiv | |
| 4 | |
| Euklidicitet | |
| 5 | |
| reflexiv | |
| T | |
| symmetrisk | |
| B | |
| sammanflytande | |
| .2 | |
| svagt ansluten | |
| .3 | |
| halveuklidiskt | |
| .3.2 | |
| R1 | |
| .4 |
Vi diskuterar axiomen ovan. Axiom 4 säger att om agenten känner till en proposition, så vet hon att hon kan den (detta axiom är också känt som "KK-principen" eller "KK-uppsatsen"). I epistemologi tenderar axiom 4 att accepteras av internalister , men inte av externalister . Axiom 4 är ändå allmänt accepterat av datavetare (men också av många filosofer, inklusive Platon , Aristoteles , Saint Augustine , Spinoza och Schopenhauer , som Hintikka minns). Ett mer kontroversiellt axiom för kunskapens logik är axiom 5 för euklidicitet: detta axiom säger att om agenten inte känner till en proposition så vet hon att hon inte vet den. De flesta filosofer (inklusive Hintikka) har angripit detta axiom, eftersom många exempel från vardagslivet verkar ogiltigförklara det. Generellt sett ogiltigförklaras axiom 5 när agenten har felaktiga uppfattningar, vilket kan bero på till exempel missuppfattningar, lögner eller andra former av bedrägeri. Axiom B anger att det inte kan vara så att agenten anser att det är möjligt att hon känner till en falsk proposition (det vill säga ). Om vi antar att axiomen T och 4 är giltiga, faller axiom B offer för samma attack som den för axiom 5 eftersom detta axiom är härledbart. Axiom D säger att agentens övertygelser är konsekventa. I kombination med axiom K (där kunskapsoperatorn ersätts med en trosoperator) är axiom D i själva verket ekvivalent med ett enklare axiom D' som förmedlar, kanske mer explicit, det faktum att agentens övertygelser inte kan vara inkonsekventa: . De andra invecklade axiomen .2, .3, .3.2 och .4 har introducerats av epistemiska logiker som Lenzen och Kutchera på 1970-talet och presenterades för några av dem som nyckelaxiom för epistemisk logik. De kan karakteriseras i termer av intuitiva interaktionsaxiom som relaterar till kunskap och övertygelser.
Axiomatisering
Hilbert- bevissystemet K för den grundläggande modala logiken definieras av följande axiom och slutledningsregler : för alla ,
| Stötta | Alla axiom och slutledningsregler för propositionell logik |
| K | |
| Nec | Om så |
Axiomen för en epistemisk logik visar uppenbarligen hur agenterna resonerar. Till exempel innebär axiomet K tillsammans med inferensregeln Nec att om jag känner till ( och jag vet att innebär ( då vet jag att ( ). Starkare begränsningar kan läggas till. Följande bevissystem för används ofta i litteraturen.
| KD45 | = | K+D+4+5 | S4.2 | = | S4+.2 | S4.3.2 | = | S4+.3.2 | S5 | = | S4+5 | |||||||||
| S4 | = | K+T+4 | S4.3 | = | S4+.3 | S4.4 | = | S4+.4 | Br | = | K+T+B |
Vi definierar uppsättningen av bevissystem .
Dessutom, för alla definierar vi bevissystemet genom att lägga till följande axiomscheman och inferensregler till de för . För alla ,
| Dis | |
| Blanda | |
| Ind |
Den relativa styrkan hos bevissystemen för kunskap är följande:
Så alla satser i är också satser för och . Många filosofer hävdar att kunskapens logik i de mest allmänna fallen är eller . Vanligtvis, inom datavetenskap och i många av teorierna som utvecklats inom artificiell intelligens, anses troslogiken ( doxastisk logik) vara och kunskapslogiken ( epstemisk logik) är tas som , även om endast är lämplig för situationer där agenterna inte har felaktiga övertygelser. har framställts av Floridi som logiken i begreppet "att bli informerad" som huvudsakligen skiljer sig från kunskapens logik genom frånvaron av introspektion för agenterna.
För alla klassen av –modeller eller –modeller är klassen av epistemiska modeller vars tillgänglighetsrelationer uppfyller de egenskaper som anges ovan definierade av axiomen för eller . Sedan, för alla H { ljud och starkt komplett för med avseende på klassen –modeller och är ljud och starkt komplett för med klassen av –modeller.
Beslutbarhet och komplexitet
Tillfredsställbarhetsproblemet för alla introducerade logiker är avgörbart . Vi listar nedan den beräkningsmässiga komplexiteten för tillfredsställbarhetsproblemet för var och en av dem. Observera att det blir linjärt i tiden om det bara finns ändligt många satsbokstäver i språket. För , om vi begränsar oss till ändlig kapsling, är tillfredsställbarhetsproblemet NP-komplett för alla modala logiker som beaktas. Om vi sedan ytterligare begränsar språket till att bara ha ändligt många primitiva satser, går komplexiteten ner till linjär i tiden i alla fall.
| Logik | med allmän kunskap | ||
|---|---|---|---|
| K, S4 | PSPACE | PSPACE | EXPTIME |
| KD45 | NP | PSPACE | EXPTIME |
| S5 | NP | PSPACE | EXPTIME |
Beräkningskomplexiteten för modellkontrollproblemet är i alla fall i P.
Lägger till dynamik
Dynamisk epistemisk logik (DEL) är ett logiskt ramverk för att modellera epistemiska situationer som involverar flera agenter, och förändringar som inträffar i dessa situationer som ett resultat av inkommande information eller mer allmänt inkommande åtgärder. Metodiken för DEL är sådan att den delar upp uppgiften att representera agenternas tro och kunskap i tre delar:
- Den ena representerar deras föreställningar om en initial situation tack vare en epistemisk modell ;
- En representerar deras uppfattning om en händelse som äger rum i denna situation tack vare en händelsemodell ;
- Den ena representerar hur agenterna uppdaterar sin uppfattning om situationen efter (eller under) händelsen, tack vare en produktuppdatering .
Vanligtvis kan en informativ händelse vara ett offentligt tillkännagivande till alla agenter av en formel : detta offentliga tillkännagivande och korrelativa uppdatering utgör den dynamiska delen. Emellertid kan epistemiska händelser vara mycket mer komplexa än enkla offentliga tillkännagivanden, inklusive att dölja information för några av agenterna, fusk, lögn, bluff, etc. Denna komplexitet behandlas när vi introducerar begreppet händelsemodell. Vi kommer först att fokusera på offentliga tillkännagivanden för att få en intuition av de huvudsakliga bakomliggande idéerna för DEL.
Offentliga evenemang
I det här avsnittet utgår vi från att alla evenemang är offentliga. Vi börjar med att ge ett konkret exempel där DEL kan användas, för att bättre förstå vad som pågår. Detta exempel kallas det leriga barnpusslet . Sedan kommer vi att presentera en formalisering av detta pussel i en logik som kallas Public Announcement Logic (PAL). Det leriga barnpusslet är ett av de mest välkända pusslen som spelade en roll i utvecklingen av DEL. Andra viktiga pussel inkluderar summan och produktpusslet , Monty Hall-dilemmat , problemet med ryska kort, problemet med två kuvert , Moores paradox , bödelparadoxen , etc.
Muddy Children Exempel:
Vi har två barn, A och B, båda smutsiga. A kan se B men inte sig själv, och B kan se A men inte sig själv. Låt vara satsen som anger att A är smutsig, och vara satsen som anger att B är smutsig.
- Vi representerar initialsituationen med den spetsiga epistemiska modellen som representeras nedan, där relationer mellan världar är ekvivalensrelationer. Tillstånd representerar intuitivt möjliga världar, en proposition (till exempel ) som är tillfredsställbar i en av dessa världar betyder intuitivt att i motsvarande möjliga värld , den intuitiva tolkningen av (A är smutsig) är sann. Länkarna mellan världar märkta av agenter (A eller B) uttrycker intuitivt en föreställning om omöjlighet att särskilja den agent som står på spel mellan två möjliga världar. Till exempel, länken mellan och märkta med A betyder intuitivt att A inte kan skilja den möjliga världen från och vice versa. A kan faktiskt inte se sig själv, så han kan inte skilja mellan en värld där han är smutsig och en där han inte är smutsig. Han kan dock skilja mellan världar där B är smutsig eller inte eftersom han kan se B. Med denna intuitiva tolkning förmås vi att anta att våra relationer mellan världar är ekvivalensrelationer.
- Anta nu att deras far kommer och meddelar att minst en är smutsig (formellt . Sedan uppdaterar vi modellen och detta ger den spetsiga epistemiska modellen som representeras nedan. Vad vi faktiskt gör är att undertrycka världar där innehållet i tillkännagivandet inte uppfylls. I vårt fall är detta världen där och är sanna. Denna undertryckning är vad vi kallar uppdateringen. Vi får då modellen avbildad nedan. Som ett resultat av tillkännagivandet vet både A och B att åtminstone en av dem är smutsig. Vi kan läsa detta från den epistemiska modellen.
- Anta nu att det finns ett andra (och sista) meddelande som säger att ingen av dem vet att de är smutsiga (ett meddelande kan uttrycka fakta om situationen såväl som epistemiska fakta om den kunskap som agenterna innehar). Vi uppdaterar sedan modellen på liknande sätt genom att undertrycka de världar som inte uppfyller innehållet i tillkännagivandet, eller på motsvarande sätt genom att behålla de världar som uppfyller tillkännagivandet. Denna uppdateringsprocess ger alltså den spetsiga epistemiska modellen som representeras nedan. Genom att tolka denna modell får vi att A och B båda vet att de är smutsiga, vilket verkar motsäga innehållet i tillkännagivandet. Men om vi antar att A och B båda är perfekta resonemang och att detta är allmänt känt bland dem, så är denna slutsats helt vettig.
Offentlig tillkännagivande logik (PAL):
Vi presenterar syntaxen och semantiken för Public Announcement Logic (PAL), som kombinerar egenskaper från epistemisk logik och propositionell dynamisk logik .
Vi definierar språket induktivt med följande grammatik i BNF :
där .
Språket tolkas över epistemiska modeller. Sanningsvillkoren för det epistemiska språkets bindemedel är desamma som i epistemisk logik (se ovan) . Sanningsvillkoret för den nya dynamiska handlingsmodaliteten definieras enligt följande:
| iff |
där med
,
för alla och
.
Formeln betyder intuitivt att efter ett sanningsenligt tillkännagivande av gäller ϕ Ett offentligt tillkännagivande av en proposition ändrar den nuvarande epistemiska modellen som i figuren nedan.
Bevissystemet som definieras nedan är bra och starkt komplett för enligt klassen för alla spetsiga epistemiska modeller.
| Axiomen och inferensreglerna för bevissystemet se ovan) | ||
| Röd 1 | ||
| röd 2 | ||
| Röd 3 | ||
| Röd 4 |
Axiomen Red 1 - Red 4 kallas reduktionsaxiom eftersom de gör det möjligt att reducera vilken formel som helst av till en bevisligen ekvivalent formel för i . Formeln är ett teorem som kan bevisas i . Den anger att efter ett offentligt tillkännagivande av vet agenten att gäller.
PAL är avgörbart , dess modellkontrollproblem är lösbart i polynomtid och dess tillfredsställbarhetsproblem är PSPACE-komplett .
Lerigt barnpussel formaliserat med PAL:
Här är några av de uttalanden som håller i det leriga barnpusslet som formaliserats i PAL.
"I utgångsläget är A smutsig och B är smutsig".
"I utgångsläget vet inte A om han är smutsig och B inte heller".
"Efter det offentliga tillkännagivandet att minst ett av barnen A och B är smutsigt vet båda att minst ett av barnen är smutsigt". Dock:
"Efter det offentliga tillkännagivandet att minst ett av barnen A och B är smutsigt vet de fortfarande inte att de är smutsiga". Dessutom:
"Efter de på varandra följande offentliga tillkännagivandena om att åtminstone ett av barnen A och B är smutsiga och att de fortfarande inte vet om de är smutsiga, vet A och B båda att de är smutsiga".
I detta sista uttalande ser vi på jobbet ett intressant inslag i uppdateringsprocessen: en formel är inte nödvändigtvis sann efter att den tillkännages. Det är vad vi tekniskt kallar "självbeständighet" och detta problem uppstår för epistemiska formler (till skillnad från propositionella formler). Man får inte blanda ihop tillkännagivandet och uppdateringen som induceras av detta tillkännagivande, vilket kan ta bort en del av informationen som kodas i meddelandet.
Godtyckliga händelser
I det här avsnittet antar vi att händelser inte nödvändigtvis är offentliga och vi fokuserar på punkterna 2 och 3 ovan, nämligen på hur man representerar händelser och på hur man uppdaterar en epistemisk modell med en sådan representation av händelser med hjälp av en produktuppdatering.
Händelsemodell
Epistemiska modeller används för att modellera hur agenter uppfattar den faktiska världen. Deras uppfattning kan också beskrivas i termer av kunskap och föreställningar om världen och om de andra agenternas tro. Insikten med DEL-upplägget är att man kan beskriva hur en händelse uppfattas av agenterna på ett väldigt likartat sätt. Agenternas uppfattning av en händelse kan faktiskt också beskrivas i termer av kunskap och övertygelser. Till exempel kan det privata tillkännagivandet av till att hennes kort är rött också beskrivas i termer av kunskap och övertygelser: medan säger till att hennes kort är rött (händelse ) tror att ingenting händer (händelse . Detta leder till att definiera begreppet händelsemodell vars definition är mycket lik den för en epistemisk modell.
En spetsig händelsemodell representerar hur den faktiska händelsen som representeras av uppfattas av agenterna. Intuitivt att medan den möjliga händelsen som representeras av inträffar, anser agent den möjliga händelsen som representeras av inträffar faktiskt.
En händelsemodell är en tuppel där:
- är en icke-tom uppsättning möjliga händelser ,
- en binär relation som kallas en tillgänglighetsrelation på , för varje ,
- precondition function assigning till varje möjlig händelse en formel för .
betecknar mängden skriver för och kallas en spetsig händelsemodell ( representerar ofta den faktiska händelsen).
Exempel på kort:
Låt oss återuppta kortexemplet och anta att spelare och visar sina kort för varandra. Det visade sig märkte att visade sitt kort till men märkte inte att gjorde det mot . Spelare och vet detta. Denna händelse representeras nedan i händelsemodellen .
Den möjliga händelsen motsvarar den faktiska händelsen 'spelare och visar sina respektive kort för varandra' (med förutsättning ), står för händelsen 'spelare visar sitt gröna kort' (med förutsättning och står för atomhändelsen 'spelare visar sitt röda kort' (med förutsättning ). Spelare och visar sina kort för varandra, spelare och vet detta och anser att det är möjligt, medan spelare anser att det är möjligt att spelare visar sitt röda kort och anser också att det är möjligt att spelare visar sitt gröna kort, eftersom han inte känner till hennes kort. Det är faktiskt allt som spelare anser vara möjligt eftersom hon inte märkte att visade sitt kort.
Ett annat exempel på händelsemodell ges nedan. Detta andra exempel motsvarar händelsen där spelare visar sitt röda kort offentligt för alla. Spelare visar sitt röda kort, spelare , och vet" det, spelare , och 'vet' att var och en av dem 'vet' det, etc. Det finns med andra ord allmän kunskap bland spelarna , och att spelare visar sitt röda kort.
Produktuppdatering
DEL-produktuppdateringen definieras nedan. Denna uppdatering ger en ny spetsig epistemisk modell representerar hur ny situation som tidigare representerades av uppfattas av agenterna efter inträffandet av händelsen representerad av .
Låt vara en epistemisk modell och låt vara en händelsemodell. Produktuppdateringen av och \ är den epistemiska modellen definieras enligt följande: för alla och alla ,
| = | ||
| = | ||
| = |
Om och är sådana att sedan betecknar den spetsiga epistemiska modellen . Denna definition av produktuppdateringen är konceptuellt grundad.
Exempel på kort:
Som ett resultat av den första händelsen som beskrivs ovan (Spelare och visar sina kort för varandra framför spelare ), uppdaterar agenterna sina övertygelser. Vi får situationen representerad i den spetsiga epistemiska modellen nedan . I denna spetsiga epistemiska modell gäller följande påstående: displaystyle vet att spelare har kortet men spelare 'tror' att det inte är fallet.
Resultatet av den andra händelsen visas nedan. I denna spetsiga epistemiska modell gäller följande uttalande: . Det sägs att det är allmänt känt bland och att de känner till världens sanna tillstånd (nämligen har det röda kortet, har det gröna kortet och har det blå kortet), men känner inte till det.
Baserat på dessa tre komponenter (epistemisk modell, händelsemodell och produktuppdatering) definierade Baltag, Moss och Solecki ett allmänt logiskt språk inspirerat av propositionell dynamisk logiks logiska språk för att resonera kring information och kunskapsförändring.
Se även
Anteckningar
- van Benthem, Johan (2011). Logisk dynamik för information och interaktion . Cambridge University Press. ISBN 978-0521873970 .
- Hans, van Ditmarsch; Halpern, Joseph; van der Hoek, Wiebe; Kooi, Barteld (2015). Handbok i epistemisk logik . London: College publikation. ISBN 978-1848901582 .
-
van Ditmarsch, Hans, van der Hoek, Wiebe, och Kooi, Barteld (2007). Dynamisk epistemisk logik . Ithaca: volym 337 av Synthese library. Springer. ISBN 978-1-4020-5839-4 .
{{ citera bok }}: CS1 underhåll: flera namn: lista över författare ( länk ) - Fagin, Ronald; Halpern, Joseph; Moses, Yoram; Vardi, Moshe (2003). Resonemang om Kunskap . Cambridge: MIT Press . ISBN 978-0-262-56200-3 . En klassisk referens.
- Hintikka, Jaakko (1962). Kunskap och tro - En introduktion till de två föreställningarnas logik . Ithaca: Cornell University Press . ISBN 978-1-904987-08-6 . .
externa länkar
- Baltag, Alexandru; Renne, Bryan. "Dynamisk epistemisk logik" . I Zalta, Edward N. (red.). Stanford Encyclopedia of Philosophy .
- van Ditmarsch, Hans; van der Hoek, Wiebe; Kooi, Barteld. "Dynamisk epistemisk logik" . Internet Encyclopedia of Philosophy .
- Hendricks, Vincent; Symons, John. "Epistemisk logik" . I Zalta, Edward N. (red.). Stanford Encyclopedia of Philosophy .
- Garson, James. "Modallogik" . I Zalta, Edward N. (red.). Stanford Encyclopedia of Philosophy .
























































































































































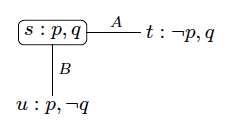


![{{\mathcal {L}}_{PAL}}:\phi ~~::=~~p~\mid ~\neg \phi ~\mid ~(\phi \land \phi )~\mid ~K_{j}\phi ~\mid ~[\phi !]\phi](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3e5867b88382755e0f4d479fa6d017a8bb284c5)
![[\psi !]\phi](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e2d92a45e41e6afc62a5e67bd24b4f27a42f133)
![{\displaystyle {\mathcal {M}},w\models [\psi !]\phi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/336da3ed0cd310a2f95561d6452e5e47e3fb6bee)








![[\psi !]p\leftrightarrow (\psi \rightarrow p)](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4e3c436287878941db025a86361369be1585682)
![[\psi !]\neg \phi \leftrightarrow (\psi \rightarrow \neg [\psi !]\phi )](https://wikimedia.org/api/rest_v1/media/math/render/svg/54a7df064b678ac79e736784ac2b980fec9f67a6)
\leftrightarrow ([\psi !]\phi \land [\psi !]\chi )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef7277529798e1134fd101f93db73f3546aeb4a7)
![[\psi !]K_{i}\phi \leftrightarrow \left(\psi \rightarrow K_{i}(\psi \rightarrow [\psi !]\phi )\right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/89657a46761034cbe5573208d974b4e5233a5d3d)
![[q!]Kq](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8e62257ae1bfa879c0d8975290ba02a2b1a5316)


\land K_{B}(p\vee q))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc4ada05c11376f8038aad786e0b6b79f49ae1dd)
\land (\neg K_{B}q\land \neg K_{B}\neg q))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/663a38eba87041a860cbb227268988bd36d74a69)
![{\displaystyle {\mathcal {N}},s\models [p\vee q!][(\neg K_{A}p\land \neg K_{A}\neg p)\land (\neg K_{B}q\land \neg K_{B}\neg q)!](K_{A}p\land K_{B}q)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c74909f6a8f28f02a243080149818b6c17823200)




































