Dissektion i ortoscheman

Olöst problem i matematik :

Kan varje simplex dissekeras till ett begränsat antal ortoscheman?

Inom geometri är det en olöst gissning av Hugo Hadwiger att varje simplex kan dissekeras till ortoschemes , med hjälp av ett antal ortoschemes som begränsas av en funktion av dimensionen av simplexen. Om det är sant, skulle mer generellt varje konvex polytop kunna dissekeras till ortoscheman.

Definitioner och uttalande

I detta sammanhang är en simplex i $d$ -dimensionell euklidisk rymd det konvexa skrovet av $d+1$ punkter som inte alla ligger i ett gemensamt hyperplan . Till exempel är en 2-dimensionell simplex bara en triangel (det konvexa skrovet av tre punkter i planet) och en 3-dimensionell simplex är en tetraeder (det konvexa av fyra punkter i det tredimensionella rummet). Punkterna som bildar simplexen på detta sätt kallas dess hörn .

Ett ortoschema, även kallat bansimplex, är en speciell sorts simplex. I den kan hörnen förbindas med en bana , så att varannan kanter i banan är i rät vinkel mot varandra. Ett tvådimensionellt ortoschema är en rätvinklig triangel . Ett tredimensionellt ortoschema kan konstrueras från en kub genom att hitta en bana av tre kanter av kuben som inte alla ligger på samma fyrkantiga yta, och forma det konvexa skrovet av de fyra punkterna på denna bana.

Dissektion av en kub i sex ortoscheman

En dissektion av en form $S$ (som kan vara vilken sluten uppsättning som helst i det euklidiska rymden) är en representation av $S$ som en förening av andra former vars interiörer är osammanhängande från varandra . Det vill säga intuitivt överlappar inte formerna i facket, även om de kan dela poäng på sina gränser. Till exempel kan en kub dissekeras i sex tredimensionella ortoscheman. Ett liknande resultat gäller mer generellt: varje hyperkub eller hyperrektangel i $d$ -dimensioner kan dissekeras till $d!$ ortoscheman.

Hadwigers gissning är att det finns en funktion $f$ så att varje $d$ -dimensionell simplex kan dissekeras till högst $f(d)$ ortoscheman. Hadwiger ställde detta problem 1956; det förblir olöst i allmänhet, även om speciella fall för små värden på $d$ är kända.

I små dimensioner

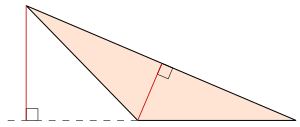
Höjden från en skarp vinkel kan misslyckas med att dissekera en triangel, men höjden från dess bredaste vinkel dissekerar den alltid i två räta trianglar

I två dimensioner kan varje triangel delas upp i högst två rätvinkliga trianglar, genom att släppa en höjd från dess bredaste vinkel till dess längsta kant.

I tre dimensioner kan vissa tetraedrar dissekeras på liknande sätt, genom att sänka en höjd vinkelrätt från en vertex $v$ till en punkt $p$ i en motsatt yta, koppla $p$ vinkelrätt till sidorna av ansiktet och använd de trekantiga vinkelräta banorna genom $v$ och $p$ till en sida och sedan till en vertex av ansiktet. Detta fungerar dock inte alltid. I synnerhet finns det tetraedrar för vilka ingen av hörnen har höjder med en fot innanför det motsatta ansiktet. Med en mer komplicerad konstruktion Lenhard (1960) att varje tetraeder kan dissekeras i högst 12 ortoscheman. Böhm (1980) bevisade att detta är optimalt: det finns tetraedrar som inte kan dissekeras i färre än 12 ortoscheman. I samma artikel generaliserade Böhm också Lenhards resultat till tredimensionell sfärisk geometri och tredimensionell hyperbolisk geometri .

I fyra dimensioner behövs som mest 500 ortoscheman. I fem dimensioner behövs återigen ett ändligt antal ortoscheman, grovt avgränsat till högst 12,5 miljoner. Återigen gäller detta sfärisk geometri och hyperbolisk geometri såväl som euklidisk geometri.

Hadwigers gissning förblir obevisad för alla dimensioner större än fem.

Konsekvenser

Varje konvex polytop kan dissekeras i simplexer. Därför, om Hadwigers gissning är sann, skulle varje konvex polytop också ha en dissektion i ortoscheman.

Ett relaterat resultat är att varje ortoschema själv kan dissekeras till $d$ eller $d+1$ mindre ortoscheman. Därför, för simplexar som kan delas upp i ortoscheman, kan deras dissektioner ha godtyckligt stort antal ortoscheman.