Coxeter komplex

I matematik är Coxeter-komplexet , uppkallat efter HSM Coxeter , en geometrisk struktur (en enkel komplex ) som är associerad med en Coxeter-grupp . Coxeter-komplex är de grundläggande objekten som tillåter uppförande av byggnader ; de utgör lägenheterna i en byggnad.

Konstruktion

Den kanoniska linjära representationen

Den första ingrediensen i konstruktionen av Coxeter-komplexet associerat med ett Coxeter-system $(W,S)$ är en viss representation av $W$ , kallad den kanoniska representationen av $W$ .

Låt $(W,S)$ vara ett Coxeter-system med Coxeter-matris $M=(m(s,t)) _{s,t\in S}$ . Den kanoniska representationen ges av ett vektorrum $V$ på grundval av formella symboler ${\displaystyle (e_{s})_{s\in S}} ,$ som är utrustad med symmetrisk bilinjär form $B(e_{s},e_{t})=-\cos \left({\frac { \pi }{m(s,t)}}\right)$ . Speciellt $B(e_{s},e_{s})=1$ . Åtgärden för $W$ på $V$ ges sedan av $s(v)=v-2B(e_ {s},v)e_{s}$ .

Denna representation har flera grundläggande egenskaper i teorin om Coxeter-grupper; till exempel $B$ positiv definitiv om och endast om $W$ är finit. Det är en trogen representation av $W$ .

Chambers och bröstkotten

Denna representation beskriver $W$ som en reflektionsgrupp , med reservationen att $B$ kanske inte är positiv definitivt. Det blir då viktigt att skilja representationen $V$ från dess dubbla $V^{*}$ . Vektorerna $e_{s}$ ligger i $V$ och har motsvarande dubbla vektorer $e_{s}^{\vee }$ i $V^{ *}$ ges av

$\langle e_{s}^{\vee },v\rangle =2B(e_{s},v),$

där de vinklade parenteserna indikerar den naturliga parningen mellan $V^{*}$ och $V$ .

Nu agerar $W$ på $V^{*}$ och åtgärden ges av

$s(f)=f-\langle f,e_{s}\rangle e_{s}^{\vee },$

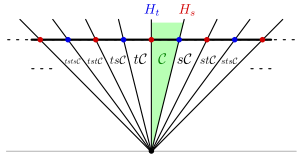
för $s\in S$ och valfri $f\in V^{*}$ . Då $s$ en reflektion i hyperplanet $H_{s}=\{f\in V^{*}:\ langle f,e_{s}\rangle =0\}$ . Man har grundkammaren ${\mathcal {C}}=\{f\in V^{*}:\langle f ,e_{s}\rangle >0\ \forall s\in S\}$ ; detta har ansikten de så kallade väggarna, $H_{s}$ . De andra kamrarna kan erhållas från ${\mathcal {C}}$ genom översättning: de är $w{\mathcal {C}}$ för $w\in W$ .

Bröstkonen är $X=\bigcup _{w\in W}w{\overline {\mathcal {C}}$ } . Detta behöver inte vara hela $V^{*}$ . Av stor betydelse är det faktum att $X$ är konvex. Stängningen ${\overline {\mathcal {C}}}$ av ${\mathcal {C}}$ är en grundläggande domän för åtgärden av $W$ på ${\ displaystil X}$ .

Coxeter-komplexet

Coxeter-komplexet $\Sigma (W,S)$ av $W$ med avseende på $S$ är ${\displaystyle \Sigma (W,S)=(X\setminus \{0\})/\mathbb {R} _{+}} , där R + {\displaystyle \mathbb {R$ } $+ }}$ är den multiplikativa gruppen av positiva realer.

Exempel

Finita dihedriska grupper

De dihedriska grupperna $D_{n}$ (av ordningen 2 n ) är Coxeter-grupper, av motsvarande typ $\mathrm {I} _{2}(n)$ . Dessa har presentationen $\left\langle s,t\,\left|\,s^{2},t^{2},(st)^{n}\right \rangle \right.$ .

Den kanoniska linjära representationen av $\mathrm {I} _{2}(n)$ är den vanliga reflektionsrepresentationen av den dihedrala gruppen, som verkar på en $n$ -gon i plan (så $V=\mathbb {R} ^{2}$ i detta fall). Till exempel, i fallet $n=3$ får vi Coxeter-gruppen av typ $\mathrm {I} _{2}(3)=\mathrm { A} _{2}$ , som verkar på en liksidig triangel i planet. Varje reflektion $s$ har ett associerat hyperplan $H_{s}$ i det dubbla vektorutrymmet (som kan kanoniskt identifieras med själva vektorutrymmet med hjälp av den bilinjära formen $B$ , som är en inre produkt i detta fall som påpekats ovan); dessa är väggarna. De skar ut kammare, som ses nedan:

Coxeter-komplexet är då motsvarande $2n$ -gon, som i bilden ovan. Detta är ett enkelt komplex av dimension 1, och det kan färgas efter samtyp.

Den oändliga dihedriska gruppen

Ett annat motiverande exempel är den oändliga dihedriska gruppen $D_{\infty }$ . Detta kan ses som gruppen av symmetrier för den reella linjen som bevarar uppsättningen av punkter med heltalskoordinater; den genereras av reflektionerna i $x=0$ och $x={1 \over 2}$ . Den här gruppen har Coxeter-presentationen $\left\langle s,t\,\left|\,s^{2},t^{2}\right\rangle \right.$ .

I det här fallet är det inte längre möjligt att identifiera $V$ med dess dubbla utrymme $V^{*}$ , eftersom $B$ är degenererad. Det är då bättre att enbart arbeta med ${\displaystyle V^{*}} ,$ som är där hyperplanen definieras. Detta ger då följande bild:

I det här fallet är bröstkonen inte hela planet, utan bara det övre halva planet. Att ta kvoten med de positiva realtalen ger sedan ytterligare en kopia av den reala linjen, med markerade punkter vid heltal. Detta är Coxeter-komplexet av den oändliga dihedriska gruppen.

Alternativ konstruktion av Coxeter-komplexet

En annan beskrivning av Coxeter-komplexet använder standardcosets av Coxeter-gruppen $W$ . En standardcoset är en coset av formen $wW_{J}$ , där $W_{J}=\langle J\rangle$ för någon delmängd $J$ av $S$ . Till exempel, $W_{S}=W$ och $W_{\emptyset }=\{1\}$ .

Coxeter-komplexet $\Sigma (W,S)$ är då poset av standardcosets, ordnade efter omvänd inkludering. Detta har en kanonisk struktur av ett förenklat komplex, liksom alla posetter som uppfyller:

• Alla två element har en största nedre gräns.
• Poseten av element som är mindre än eller lika med ett givet element är isomorf till poseten av delmängder av $\{1,2,\ldots ,n\}$ för något heltal n .

Egenskaper

Coxeter-komplexet associerat med $(W,S)$ har dimension $|S|-1$ . Det är homeomorft till en $(|S|-1)$ -sfär om W är finit och är sammandragbar om W är oändlig.

Se även

• Byggnader
• Weyl-gruppen
• Rotsystem

• Peter Abramenko och Kenneth S. Brown , Byggnader, teori och tillämpningar . Springer, 2008.