Chans algoritm

En 2D-demo för Chans algoritm. Observera dock att algoritmen delar upp punkterna godtyckligt, inte med x-koordinat.

Inom beräkningsgeometri är Chans algoritm , uppkallad efter Timothy M. Chan , en optimal utdatakänslig algoritm för att beräkna det konvexa skrovet för en uppsättning $P$ av $n$ punkter, i 2- eller 3- dimensionellt utrymme. Algoritmen tar $O(n\log h)$ tid, där $h$ är antalet hörn av utmatningen (det konvexa skrovet). I det plana fallet kombinerar algoritmen en $O(n\log n)$ algoritm ( Graham scan , till exempel) med Jarvis march ( $O(nh ) )$ ), för att erhålla en optimal $O(n\log h)$ tid. Chans algoritm är anmärkningsvärd eftersom den är mycket enklare än Kirkpatrick–Seidel-algoritmen och den sträcker sig naturligtvis till 3-dimensionell rymd. Detta paradigm har utvecklats oberoende av Frank Nielsen i sin doktorsexamen. avhandling.

Algoritm

Översikt

En enda pass av algoritmen kräver en parameter $m$ som är mellan 0 och $n$ (antal punkter i vår uppsättning $P$ ). Helst är $m=h$ men ${\displaystyle h} ,$ antalet hörn i det utgående konvexa skrovet, är inte känt i början. Flera pass med ökande värden på $m$ görs som sedan avslutas när $m\geq h$ (se nedan om val av parameter $m$ ).

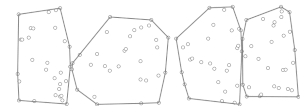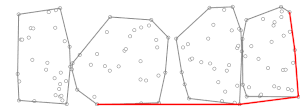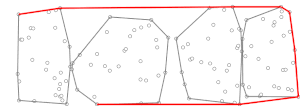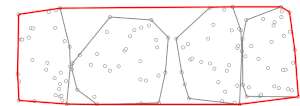
Algoritmen börjar med att godtyckligt partitionera uppsättningen av punkter $P$ i $K=\lceil n/m\rceil$ delmängder $(Q_{k})_{k=1,2,...K}$ med högst $m$ punkter vardera; Lägg märke till att $K=O(n/m)$ .

För varje delmängd $Q_{k}$ beräknar den det konvexa skrovet, $C_{k}$ , med hjälp av en $O(p\log p)$ algoritm (till exempel Graham scan ), där $p$ är antalet punkter i delmängden. Eftersom det finns $K$ delmängder av $O(m)$ punkter vardera, tar denna fas $K \cdot O(m\log m)=O(n\log m)$ tid.

Under den andra fasen avrättas Jarvis marsch , med användning av de förberäknade (mini) konvexa skroven, $(C_{k})_{k=1,2,...K}$ . Vid varje steg i denna Jarvis marschalgoritm har vi en punkt $p_{i}$ i det konvexa skrovet (i början kan $p_{i}$ vara punkten i ${\ displaystyle P}$ med den lägsta y-koordinaten, som garanterat finns i det konvexa skrovet av $P$ ), och behöver hitta en punkt $p_{ i+1}=f(p_{i},P)$ så att alla andra punkter i $P$ är till höger om linjen $p_{i}p_{i +1}$ , där notationen $p_{i+1}=f(p_{i},P)$ betyder helt enkelt att nästa punkt , det vill säga $p_{i+1}$ , bestäms som en funktion av $p_{i}$ och $P$ . Det konvexa skrovet för uppsättningen $Q_{k}$ , ${\displaystyle C_{k}} ,$ är känt och innehåller högst $m$ punkter (listade i en medurs eller moturs ordning), vilket gör det möjligt att beräkna $f(p_{i},Q_{k})$ i $O(\log m)$ tid med binär sökning . Därför kan beräkningen av $f(p_{i},Q_{k})$ för alla $K$ i $O(K\log m)$ tid. Sedan kan vi bestämma $f(p_{i},P)$ med samma teknik som normalt används i Jarvis's marsch, men bara med tanke på punkterna ${\displaystyle (f(p_{i},Q_{k}))_{1\leq k\leq K}} (dvs punkterna$ i de minikonvexa skroven) istället för hela uppsättningen $P$ . För dessa punkter är en iteration av Jarvis's marsch $O(K)$ vilket är försumbart jämfört med beräkningen för alla delmängder. Jarvis marsch avslutas när processen har upprepats $O(h)$ gånger (eftersom, på det sätt som Jarvis march fungerar, efter högst $h$ iterationer av dess yttersta slinga, där ${ \displaystyle h}$ är antalet punkter i det konvexa skrovet av $P$ , vi måste ha hittat det konvexa skrovet), därför tar den andra fasen $O(Kh\ log m)$ tid, motsvarande $O(n\log h)$ tid om $m$ är nära $h$ (se nedan beskrivning av en strategi för att välja $m$ så att detta är fallet).

Genom att köra de två faserna som beskrivs ovan, beräknas det konvexa skrovet av ${\displaystyle n} punkter i$$O(n\log h)$ tid.

Att välja parametern ${\textstyle m}$

Om ett godtyckligt värde väljs för $m$ , kan det hända att $m<h$ . I så fall, efter $m$ steg i den andra fasen, avbryter vi Jarvis marsch eftersom det skulle ta för lång tid att köra den till slutet. I det ögonblicket kommer en $O(n\log m)$ tid att ha spenderats, och det konvexa skrovet kommer inte att ha beräknats.

Tanken är att göra flera pass av algoritmen med ökande värden på $m$ ; varje pass avslutas (framgångsrikt eller misslyckat) i $O(n\log m)$ tid. Om $m$ ökar för långsamt mellan omgångarna, kan antalet iterationer vara stort; å andra sidan, om den stiger för snabbt kan den första $m$ för vilken algoritmen avslutas framgångsrikt vara mycket större än $h$ , och ge en komplexitet $O(n\log m)>O(n\log h)$ .

Kvadreringsstrategi

En möjlig strategi är att kvadrera värdet på $m$ vid varje iteration, upp till ett maximalt värde på $n$ (motsvarande en partition i singleton-uppsättningar). Med utgångspunkt från värdet 2, vid iteration $t$ , $m=\min \left(n,2^{2^{t}}\right)$ väljs. I så fall görs ${\displaystyle O(\log \log h)} iterationer, givet att algoritmen avslutas när vi har$

$_ =2^{2^{t}}\geq h\iff \log \left(2^{2^{t}}\right)\geq \log h\iff 2^{t}\geq \log h\ iff \log {2^{t}}\geq \log {\log h}\iff t\geq \log {\log h},}$

med logaritmen tagen i bas $2$ , och den totala körtiden för algoritmen är

$\sum _{t=0}^{\lceil \log \log h\rceil}O\left(n\log \left(2^{2^{t}}\right)\right)=O (n)\summa _{t=0}^{\lceil \log \log h\rceil }2^{t}=O\left(n\cdot 2^{1+\lceil \log \log h\rceil }\right)=O(n\log h).$

I tre dimensioner

För att generalisera denna konstruktion för det 3-dimensionella fallet bör en ${\displaystyle O(n\log n)}-$ algoritm för att beräkna det 3-dimensionella konvexa skrovet av Preparata och Hong användas istället för Graham-skanning , och en 3-dimensionell version av Jarviss marsch måste användas. Tidskomplexiteten förblir $O(n\log h)$ .

Pseudokod

I följande pseudokod är text mellan parenteser och i kursiv stil kommentarer. För att till fullo förstå följande pseudokod, rekommenderas det att läsaren redan är bekant med Graham scan och Jarvis march -algoritmer för att beräkna det konvexa skrovet, ${\displaystyle C} ,$ av en uppsättning punkter, $P$ .

Inmatning: Ställ in $P$ med $n$ punkter.

Utdata: Ställ in $C$ med $h$ -punkter, det konvexa skrovet på $P$ .

(Välj en punkt av $P$ som garanterat är i $C$ : till exempel punkten med den lägsta y-koordinaten.)

(Denna operation tar ${\mathcal {O}}(n)$ tid: t.ex. kan vi helt enkelt iterera genom $P$ .)

$p_{1}: =PICK\_START(P)$

( $p_{0}$ används i Jarvis march-delen av denna Chans algoritm,

så att för att beräkna den andra punkten, $p_{2}$ , i det konvexa skrovet på $P$ .)

(Obs! $p_{0}$ är inte en punkt av $P$ .)

(För mer information, se kommentarerna nära motsvarande del av Chans algoritm.)

$p_{0}:=(-\infty ,0)$

(Notera: $h$ , antalet punkter i det slutliga konvexa skrovet av $P$ , är inte känd.)

(Detta är iterationerna som behövs för att upptäcka värdet av $m$ , vilket är en uppskattning av $h$ .)

( ${\ displaystyle h\leq m}$ krävs för att denna Chans algoritm ska hitta det konvexa skrovet för ${\displaystyle P} .$ )

(Mer specifikt vill vi ha $h\leq m\leq h^{ 2}$ , för att inte utföra för många onödiga iterationer

och så att tidskomplexiteten för denna Chans algoritm är ${\displaystyle {\mathcal {O}}(n\log h)} .$ )

(Som förklarat ovan i den här artikeln används en strategi där som mest $\log \log n$ iterationer krävs för att hitta $m$ .)

(Obs: den sista ${\ displaystyle m}$ kanske inte är lika med $h$ , men den är aldrig mindre än $h$ och större än $h^{2}$ .)

(Ändå stoppar denna Chans algoritm när $h$ iterationer av den yttersta slingan har utförts,

det vill säga även om $m\neq h$ utförs inte $m$ iterationer av den yttersta slingan.)

(För mer information, se Jarvis-marschdelen av denna algoritm nedan, där $C$ returneras om $p_{i+1}==p_{1}$ . )

för $1\leq t\leq \log \log n$ do

(Ställ in parameter $m$ för den aktuella iterationen. Ett "kvadreringsschema" används enligt beskrivningen ovan i den här artikeln.

Det finns andra scheman: till exempel "fördubblingsschemat", där $m=2^{t}$ , för $t=1, \dots ,\left\lceil \log h\right\rceil$ .

Om "dubbleringsschemat" används är den resulterande tidskomplexiteten för denna Chans algoritm ${\mathcal {O}}(n\log ^{2}h)$ . )

$m:=2^{2^{t}}$

(Initiera en tom lista (eller array) för att lagra punkterna för det konvexa skrovet på $P$ , eftersom de finns.)

$C:=()$

$ADD(C,p_{1})$

(Godyckligt delad uppsättning punkter $P$ till $K=\left\lceil {\frac {n}{m}}\right\rceil$ delmängder av ungefär $m$ element vardera.)

$Q_{1},Q_{2},\dots ,Q_{K}:=SPLIT(P,m)$

(beräkna konvext skrov av alla $K$ delmängder av punkter, $Q_{1},Q_{2},\dots ,Q_{K}$ .)

(Det tar ${\displaystyle {\mathcal {O}}(Km\log m)={\mathcal {O}}(n\log m)} tid.$ )

Om $m\leq h^{2}$ så är tidskomplexiteten ${\mathcal {O}}( n\log h^{2})={\mathcal {O}}(n\log h)$ .)

för $1\leq k\leq K$ do

(beräkna det konvexa skrovet för delmängd $k$ , $Q_{k}$ , med Graham-skanning, som tar ${\mathcal {O}}(m\log m)$ tid .)

( $C_{k}$ är det konvexa skrovet av delmängden av punkter $Q_{k}$ .)

$C_{k}:=GRAHAM\_SCAN(Q_{k})$

(Vid denna punkt, de konvexa skroven $C_{1}, C_{ 2},\dots ,C_{K}$ av respektive delmängder av punkterna $Q_{1},Q_{2},\dots ,Q_{K}$ har varit beräknad.)

(Använd nu en modifierad version av Jarvis march -algoritmen för att beräkna det konvexa skrovet för ${\displaystyle P} .$ )

(Jarvis march uppträder i ${\mathcal {O}}( nh)$ tid, där $n$ är antalet inmatningspunkter och $h$ är antalet punkter i det konvexa skrovet.)

(Med tanke på att Jarvis march är en utdatakänslig algoritm , kör den tiden beror på storleken på det konvexa skrovet, ${\displaystyle h} .$ )

(I praktiken betyder det att Jarvis march utför $h$ iterationer av sin yttersta slinga.

Vid var och en av dessa iterationer utför den högst $n$ iterationer av sin innersta slinga.)

(Vi vill ha $h\leq m\leq h^{2}$ , så vi vill inte utföra fler än $m$ iterationer i följande yttre slinga.)

(Om den aktuella $m$ är mindre än $h$ , dvs $m< h$ , det konvexa skrovet på $P$ kan inte hittas.)

(I denna modifierade version av Jarvis march utför vi en operation inuti den innersta slingan som tar ${\mathcal { O}}(\log m)$ tid.

Därför är den totala tidskomplexiteten för denna modifierade version

${\mathcal {O}}(mK\log m)={\mathcal {O}}(m\left\lceil {\ frac {n}{m}}\right\rceil \log m)={\mathcal {O}}(n\log m)={\mathcal {O}}(n\log 2^{2^{t} })={\mathcal {O}}(n2^{t}).$

Om $m\leq h^{2}$ , då är tidskomplexiteten ${\displaystyle {\mathcal {O}}(n\log h^{2})={\mathcal {O}}(n\log h)} .$ )

för $1\leq i\leq m$ do

(Obs: här är en punkt i det konvexa skrovet av $P$ redan känd, det vill säga $p_{1}$ .)

( I denna inre for- loop kan $K$ möjliga nästa punkter vara på det konvexa skrovet av $P$ , ${\displaystyle q_{ i,1},q_{i,2},\dots ,q_{i,K}} ,$ beräknas.)

(Var och en av dessa $K$ möjliga nästa punkter kommer från en annan $C_ {k}$ :

det vill säga $q_{i,k}$ är en möjlig nästa punkt på det konvexa skrovet av $P$ som är en del av det konvexa skrovet av ${\ displaystyle C_{k}}$ .)

(Obs: $q_{i,1},q_{i,2},\dots ,q_{i ,K}$ beror på $i$ : det vill säga för varje iteration $i$ , finns det $K$ möjliga nästa punkter på det konvexa skrovet av $P$ .)

(Obs: vid varje iteration $i$ , endast en av punkterna bland $q_{i,1},q_{i ,2},\dots ,q_{i,K}$ läggs till det konvexa skrovet av $P$ .)

för $1\leq k\leq K$ do

( $JARVIS\_BINARY\_SEARCH$ hittar punkten $d\in C_{k}$ så att vinkeln $\measuredangle p_{i-1}p_{i}d$ är maximerad ,

där $\measuredangle p_{i-1}p_{i}d$ är vinkeln mellan vektorerna ${\overrightarrow {p_{ i}p_{i-1}}}$ och ${\overrightarrow {p_{i}d}}$ . Sådan $d$ lagras i ${\displaystyle q_{i,k}} .$ )

(Vinklar behöver inte beräknas direkt: orienteringstestet kan användas .)

( $JARVIS\_BINARY\_SEARCH$ kan utföras i ${\mathcal {O}}(\ log m)$ tid .)

(Obs: vid iterationen $i=1$ , $p_{i-1}= p_{0}=(-\infty ,0)$ och $p_{1}$ är kända och är en punkt i det konvexa skrovet av $P$ :

i detta fall är det punkten av $P$ med den lägsta y-koordinaten.)

${\displaystyle q_{i,k}:=JARVIS\_BINARY\_SEARCH(p_{i-1},p_{i},C_{k})} (Välj$

punkten ${\displaystyle z\in \{q_{i,1},q_{i,2},\dots ,q_{i,K}\}} vilket maximerar$ vinkeln ${\displaystyle \measuredangle p_{i-1}p_{i}z} [$ för att vara nästa punkt på det konvexa skrovet av $P$ .)

$p_{i+1}:=JARVIS\_NEXT\_CH\_POINT(p_{i-1},p_{i},(q_{i,1},q_{i,2},\dots ,q_ {i,K}))$

(Jarvis march avslutas när nästa valda punkt på det konvexa skrovet, $p_{i+1}$ , är startpunkten, $p_{1 }$ .)

om $p_{i+1}==p_{1}$

(Återställ det konvexa skrovet på $P$ som innehåller $i =h$ poäng.)

(Obs: naturligtvis behöver du inte returnera $p_{i+1}$ vilket är lika med $p_{1}$ .)

return $C:=(p_{1},p_{2},\dots ,p_{i})$

annars

$ADD(C,p_{i+1})$

(Om en punkt $p_{i+1}$ inte har hittats efter ${\displaystyle m} iterationer så att$$p_{i+1}==p_{1}$ , sedan $m<h$ .)

(Vi måste börja om med ett högre värde för $m$ .)

Genomförande

Chans papper innehåller flera förslag som kan förbättra algoritmens praktiska prestanda, till exempel:

• När du beräknar de konvexa skroven för delmängderna, eliminera de punkter som inte finns i det konvexa skrovet från beaktande vid efterföljande avrättningar.
• De konvexa skroven av större punktuppsättningar kan erhållas genom att slå samman tidigare beräknade konvexa skrov, istället för att räkna om från grunden.
• Med ovanstående idé ligger den dominerande kostnaden för algoritmen i förbearbetningen, dvs. beräkningen av gruppernas konvexa skrov. För att minska denna kostnad kan vi överväga att återanvända skrov som beräknats från föregående iteration och slå samman dem när gruppstorleken ökar.

Tillägg

Chans papper innehåller några andra problem vars kända algoritmer kan göras optimalt utdatakänsliga med hans teknik, till exempel:

• Beräknar det nedre enveloppet $L(S)$ för en uppsättning $S$ av $n$ linjesegment, som definieras som den nedre gränsen för den ogränsade trapets som bildas av korsningar.
• Hershberger gav en ${\displaystyle O(n\log n)}-$ algoritm som kan snabbas upp till $O(n\log h)$ , där h är antalet kanter i kuvertet

• Konstruera utdatakänsliga algoritmer för högre dimensionella konvexa skrov. Med användning av grupperingspunkter och effektiva datastrukturer ${\displaystyle O(n\log h)}-$ komplexitet uppnås förutsatt att h är av polynomordning i $n$ .

Se även

• Konvexa skrovalgoritmer