Graham skanning

En demo av Grahams skanning för att hitta ett 2D konvext skrov.

Grahams skanning är en metod för att hitta det konvexa skrovet av en ändlig uppsättning punkter i planet med tidskomplexitet O ( n log n ). Den är uppkallad efter Ronald Graham , som publicerade den ursprungliga algoritmen 1972. Algoritmen hittar alla hörn av det konvexa skrovet ordnade längs dess gräns. Den använder en stack för att detektera och ta bort konkaviteter i gränsen effektivt.

Algoritm

Som man kan se är PAB och ABC moturs, men BCD är det inte. Algoritmen upptäcker denna situation och kasserar tidigare valda segment tills svängen som tas är moturs (ABD i detta fall.)

Det första steget i denna algoritm är att hitta punkten med den lägsta y-koordinaten. Om den lägsta y-koordinaten finns i mer än en punkt i mängden, bör den punkt med den lägsta x-koordinaten av kandidaterna väljas. Kalla denna punkt P . Detta steg tar O ( n ), där n är antalet poäng i fråga.

Därefter måste uppsättningen av punkter sorteras i ökande ordning efter vinkeln de och punkten P gör med x-axeln. Alla generella sorteringsalgoritmer är lämpliga för detta, till exempel heapsort (som är O( n log n )).

Sortering i vinkelordning kräver inte beräkning av vinkeln. Det är möjligt att använda vilken funktion av vinkeln som helst som är monoton i intervallet $[0,\pi ]$ . Cosinus beräknas enkelt med hjälp av punktprodukten , eller så kan linjens lutning användas. Om numerisk precision står på spel kan jämförelsefunktionen som används av sorteringsalgoritmen använda tecknet för korsprodukten för att bestämma relativa vinklar.

Om flera punkter har samma vinkel, bryt antingen banden genom att öka avståndet ( Manhattan- eller Chebyshev -avståndet kan användas istället för euklidiskt för enklare beräkning, eftersom punkterna ligger på samma stråle), eller ta bort alla utom den längsta punkten.

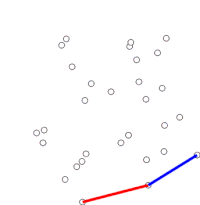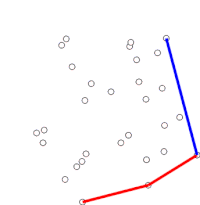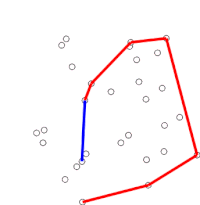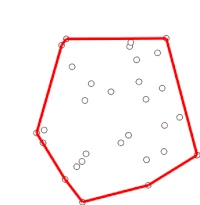
Algoritmen fortsätter genom att betrakta var och en av punkterna i den sorterade matrisen i sekvens. För varje punkt bestäms det först om färden från de två punkterna omedelbart före denna punkt utgör en vänstersväng eller en högersväng. Om en högersväng är den näst sista punkten inte en del av det konvexa skrovet, och ligger "inuti" det. Samma bestämning görs sedan för uppsättningen av den senaste punkten och de två punkter som omedelbart föregår punkten som konstaterats ha varit inuti skrovet, och upprepas tills en "vänstersväng" uppsättning påträffas, vid vilken punkt algoritmen går vidare till nästa punkt i uppsättningen av punkter i den sorterade arrayen minus eventuella punkter som befanns vara inuti skrovet; det finns ingen anledning att överväga dessa punkter igen. (Om de tre punkterna i något skede är kolinjära kan man välja att antingen kassera eller rapportera det, eftersom det i vissa tillämpningar krävs att man hittar alla punkter på gränsen för det konvexa skrovet.)

Återigen, att bestämma huruvida tre punkter utgör en "vänstersväng" eller en "högersväng" kräver inte beräkning av den faktiska vinkeln mellan de två linjesegmenten, och kan faktiskt endast uppnås med enkel aritmetik. För tre punkter $P_{1}=(x_{1},y_{1})$ , $P_{2 }=(x_{2},y_{2})$ och $P_{3}=(x_{3},y_{3})$ , beräkna z - koordinat för korsprodukten av de två vektorerna ${\overrightarrow {P_{1}P_{2}}}$ och ${\overrightarrow {P_{1}P_ {3}}}$ , som ges av uttrycket $(x_{2} -x_{1})(y_{3}-y_{1})-(y_{2}-y_{1})(x_{3}-x_{1})$ . Om resultatet är 0, är ​​punkterna kolinjära; om den är positiv utgör de tre punkterna en "vänstersväng" eller moturs orientering, annars en "högersväng" eller en medurs orientering (för moturs numrerade punkter).

Denna process kommer så småningom att återgå till den punkt där den började, vid vilken punkt algoritmen är klar och stacken innehåller nu punkterna på det konvexa skrovet i moturs ordning.

Tidskomplexitet

Att sortera punkterna har tidskomplexitet O( n log n ). Även om det kan tyckas att slingans tidskomplexitet är O( n ² ), eftersom den för varje punkt går tillbaka för att kontrollera om någon av de föregående punkterna gör en "högersväng", är den faktiskt O( n ), eftersom varje punkt punkt anses högst två gånger i någon mening. Varje punkt kan endast visas en gång som en punkt $(x_{2},y_{2})$ i en "vänstersväng" (eftersom algoritmen går vidare till nästa punkt $(x_{3},y_{3})$ efter det), och som en punkt $(x_{2},y_{2})$ i en "högersväng" (eftersom punkten $(x_{2},y_{2})$ är borttagen). Den totala tidskomplexiteten är därför O( n log n ), eftersom tiden att sortera dominerar tiden för att faktiskt beräkna det konvexa skrovet.

Pseudokod

Pseudokoden nedan använder en funktion ccw: ccw > 0 om tre punkter gör en vridning moturs, medurs om ccw < 0, och kolinjär om ccw = 0. (I verkliga tillämpningar, om koordinaterna är godtyckliga reella tal, kräver funktionen exakt jämförelse av flyttal, och man måste akta sig för numeriska singulariteter för "nästan" kolinjära punkter.)

Låt sedan resultatet lagras i traven .

  låt  punkter  vara  listan med punkter  låt  stack = empty_stack()  hitta  den lägsta y-koordinaten och punkten längst till vänster, kallad P0  sortera  punkter efter polär vinkel med P0, om flera punkter har samma polära vinkel så håll bara den längst bort  för  punkt  i  punkter : # pop den sista punkten från stapeln om vi vrider medurs för att nå denna punkt  medan  count  stack > 1 och  ccw  (next_to_top(stack), top(stack), point) <= 0:  pop  stack  push  point  to  stack  end 

Nu innehåller traven det konvexa skrovet, där punkterna är orienterade moturs och P0 är den första punkten.

Här är next_to_top() en funktion för att returnera objektet en post under toppen av stacken, utan att ändra stacken, och på liknande sätt top() för att returnera det översta elementet.

Denna pseudokod är anpassad från Introduktion till algoritmer .

Anteckningar

Samma grundidé fungerar även om inmatningen sorteras på x-koordinat istället för vinkel, och skrovet beräknas i två steg som producerar den övre respektive den nedre delen av skrovet. Denna modifiering utarbetades av AM Andrew. Den har samma grundläggande egenskaper som Grahams skanning.

Grahams ursprungliga beskrivning involverade sortering runt en inre punkt av det konvexa skrovet , snarare än en av dess hörn. För samma val av en pivotpunkt för sorteringsalgoritmen, att ansluta alla de andra punkterna i deras sorterade ordning runt denna punkt istället för att utföra de återstående stegen av Graham-skanningen producerar en stjärnformad polygon , en polygonalisering av inmatningen.

Stacktekniken som används i Grahams skanning är mycket lik den för problemet med alla närmaste mindre värden , och parallella algoritmer för alla närmaste mindre värden kan också användas (som Grahams skanning) för att effektivt beräkna konvexa skrov av sorterade sekvenser av punkter.

Numerisk robusthet

Numerisk robusthet är ett problem att ta itu med i algoritmer som använder ändlig precision med flyttal . Ett dokument från 2004 analyserade en enkel inkrementell strategi, som i synnerhet kan användas för en implementering av Graham-skanningen. Det uttalade målet med uppsatsen var inte att specifikt analysera algoritmen, utan snarare att ge ett läroboksexempel på vad och hur kan misslyckas på grund av flyttalsberäkningar i beräkningsgeometri . Senare utvecklade D. Jiang och NF Stewart detta och drog två primära slutsatser med hjälp av bakåtfelsanalysen . Den första är att det konvexa skrovet är ett välkonditionerat problem, och därför kan man förvänta sig algoritmer som ger ett svar inom en rimlig felmarginal. För det andra visar de att en modifiering av Graham-skanningen som de kallar Graham-Fortune (som innehåller idéer från Steven Fortune för numerisk stabilitet) övervinner problemen med ändlig precision och inexakta data "i vilken utsträckning det än är möjligt att göra det".

Se även

• Konvexa skrovalgoritmer

Vidare läsning

•   Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. ; Stein, Clifford (2001) [1990]. "33.3: Hitta det konvexa skrovet". Introduktion till algoritmer (2:a upplagan). MIT Press och McGraw-Hill. s. 949–955. ISBN 0-262-03293-7 .