Brytningsindex och extinktionskoefficient för tunnfilmsmaterial

AR Forouhi och I. Bloomer härledde dispersionsekvationer för brytningsindex, n , och extinktionskoefficient, k , som publicerades 1986 och 1988. 1986 års publikation avser amorfa material, medan 1988 års publikation avser kristallina. Därefter, 1991, ingick deras arbete som ett kapitel i "The Handbook of Optical Constants". Forouhi –Bloomer dispersionsekvationer beskriver hur fotoner med varierande energi interagerar med tunna filmer. När de används med ett spektroskopiskt reflektometriverktyg specificerar Forouhi–Bloomer dispersionsekvationer n och k för amorfa och kristallina material som en funktion av fotonenergin E . Värden på n och k som funktion av fotonenergi, E , benämns spektra för n och k , vilket också kan uttryckas som funktioner av ljusets våglängd, λ, eftersom E = HC/λ . Symbolen h representerar Plancks konstant och c , ljusets hastighet i vakuum. Tillsammans kallas n och k ofta för de "optiska konstanterna" för ett material (även om de inte är konstanter eftersom deras värden beror på fotonenergi).

Härledningen av Forouhi–Bloomer dispersionsekvationer är baserad på att erhålla ett uttryck för k som en funktion av fotonenergi, symboliskt skrivet som k (E), med utgångspunkt från de första principerna kvantmekanik och fasta tillståndets fysik. Ett uttryck för n som en funktion av fotonenergi, symboliskt skrivet som n (E), bestäms sedan från uttrycket för k (E) i enlighet med Kramers-Kronig-relationerna som säger att n (E) är Hilbert-transformen av k (E).

Forouhi–Bloomer dispersionsekvationer för n (E) och k (E) av amorfa material ges som:

$k(E)={\frac {A(E-E_{g})^{2}}{E^{ 2}-BE+C}}\$

$n(E)=n(\infty )+{\frac {(B_{0}E+C_{ 0})}{E^{2}-BE+C}}\$

₀₀ De fem parametrarna A, B, C, Eg _och n ( ∞) har var och en fysisk betydelse. Eg är materialets optiska energibandgap _. A, B och C beror på materialets bandstruktur. De är positiva konstanter så att 4C-B ² > 0. Slutligen representerar n(∞), en konstant större än enhet, värdet på n vid E = ∞. Parametrarna B och C i ekvationen för n (E) är inte oberoende parametrar, utan beror på A, B, C och E _g . De ges av:

$B_{0}={\frac {A}{Q}}\ \left({\frac {-B^{ 2}}{2}}\ +E_{g}B-{E_{g}}^{2}+C\höger)$

$C_{0}={\frac {A}{Q}}\ \left[({E_{g}}^ {2}+C){\frac {B}{2}}\ -2E_{g}C\höger]$

var

$Q={\frac {1}{2}}\ (4C-B^{2})^{\frac {1}{2}}$

Således, för amorfa material, är totalt fem parametrar tillräckliga för att fullständigt beskriva beroendet av både n och k på fotonenergi, E.

För kristallina material som har flera toppar i sina n- och k- spektra, kan Forouhi-Bloomer-dispersionsekvationerna utökas enligt följande:

$k(E)=\summa _{i=1}^{q }\left[{\frac {A_{i}(E-E_{g_{i}})^{2}}{E^{2}-B_{i}E+C_{i}}}\höger]$

$n(E)=n(\infty )+\summa _{ i=1}^{q}\left[{\frac {B_{0_{i}}E+C_{0_{i}}}{E^{2}-B_{i}E+C_{i}} }\höger]$

₀₀ Antalet termer i varje summa, q, är lika med antalet toppar i materialets n- och k -spektra. Varje term i summan har sina egna värden för parametrarna A, B, C, E _g , samt sina egna värden för B och C . Analogt med det amorfa fallet har termerna alla fysisk betydelse.

Karakteriserande tunna filmer

Brytningsindex ( n ) och extinktionskoefficient ( k ) är relaterade till interaktionen mellan ett material och infallande ljus, och är associerade med brytning och absorption (respektive). De kan betraktas som "materialets fingeravtryck". Beläggningar av tunnfilmsmaterial på olika substrat ger viktiga funktioner för mikrotillverkningsindustrin, och n , k , såväl som tjockleken t , av dessa tunnfilmsbeståndsdelar måste mätas och kontrolleras för att möjliggöra repeterbar tillverkning .

Forouhi-Bloomer dispersionsekvationerna för n och k förväntades ursprungligen gälla för halvledare och dielektrika, vare sig de var i amorfa, polykristallina eller kristallina tillstånd. De har dock visat sig beskriva n- och k -spektra för transparenta ledare, såväl som metalliska föreningar. Formalismen för kristallina material visade sig gälla även för polymerer, som består av långa kedjor av molekyler som inte bildar en kristallografisk struktur i klassisk mening.

Andra dispersionsmodeller som kan användas för att härleda n och k , såsom Tauc–Lorentz-modellen , finns i litteraturen. Två välkända modeller - Cauchy och Sellmeier - tillhandahåller empiriska uttryck för n som är giltiga över ett begränsat mätområde och är endast användbara för icke-absorberande filmer där k =0. Följaktligen har Forouhi–Bloomer-formuleringen använts för att mäta tunna filmer i olika applikationer.

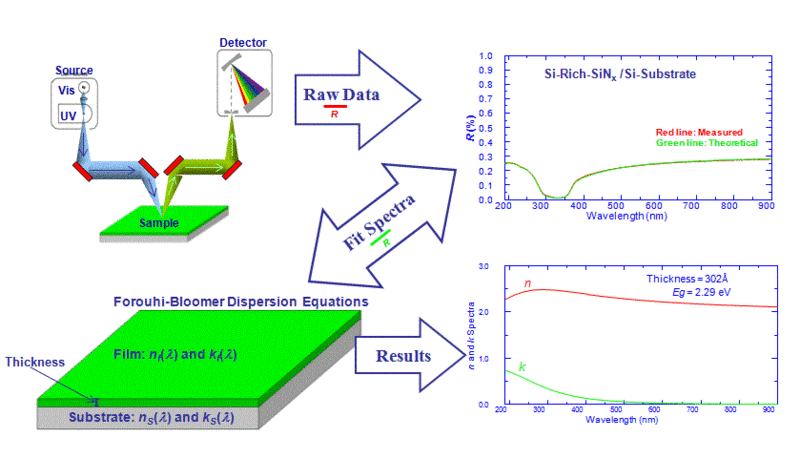
I de följande diskussionerna kommer alla variabler för fotonenergi, E , att beskrivas i termer av ljusets våglängd, λ, eftersom experimentella variabler som involverar tunna filmer typiskt mäts över ett spektrum av våglängder. n- och k -spektra för en tunn film kan inte mätas direkt, utan måste bestämmas indirekt från mätbara storheter som beror på dem . Spektroskopisk reflektans, R(λ ), är en sådan mätbar storhet. En annan är spektroskopisk transmittans, T(λ) , tillämpbar när substratet är transparent. Spektroskopisk reflektans för en tunn film på ett substrat representerar förhållandet mellan intensiteten av ljus som reflekteras från provet och intensiteten av infallande ljus, mätt över ett intervall av våglängder, medan spektroskopisk transmittans, T(λ) , representerar förhållandet mellan intensiteten av ljus som sänds genom provet till intensiteten av infallande ljus, mätt över ett intervall av våglängder; typiskt kommer det också att finnas en reflekterad signal, R(λ) , som åtföljer T(λ) .

De mätbara storheterna, R(λ) och T(λ) beror inte bara på n(λ) och k(λ) av filmen, utan också på filmtjockleken, t , och n(λ) och k(λ) av filmen substrat. För ett kiselsubstrat n(λ)- och k(λ) -värdena kända och tas som en given ingång. Utmaningen med att karakterisera tunna filmer innebär att extrahera t , n(λ) och k(λ) av filmen från mätningen av R(λ) och/eller T(λ) . Detta kan uppnås genom att kombinera Forouhi-Bloomer-spridningsekvationerna för n(λ) och k(λ) med Fresnel-ekvationerna för reflektion och transmission av ljus vid ett gränssnitt för att erhålla teoretiska, fysiskt giltiga, uttryck för reflektans och transmittans. På så sätt reduceras utmaningen till att extrahera de fem parametrarna A, B, C, E _g och n(∞) som utgör n(λ) och k(λ) tillsammans med filmtjockleken t genom att använda en olinjär minsta kvadraters regressionsanalys anpassningsprocedur. Anpassningsproceduren innebär en iterativ förbättring av värdena för A, B, C, E g _, n (∞) , t , för att reducera summan av kvadraterna av felen mellan den teoretiska R(λ) eller den teoretiska T( λ) och det uppmätta spektrumet av R(λ) eller T(λ) .

Förutom spektroskopisk reflektans och transmittans kan spektroskopisk ellipsometri också användas på ett analogt sätt för att karakterisera tunna filmer och bestämma t , n(λ) och k(λ) .

Mätningsexempel

Följande exempel visar mångsidigheten i att använda Forouhi–Bloomer dispersionsekvationer för att karakterisera tunna filmer med hjälp av ett verktyg baserat på nästan normal infallande spektroskopisk reflektans. Nästan normal spektroskopisk transmittans används också när substratet är transparent. n (λ)- och k(λ) -spektra för varje film erhålls tillsammans med filmtjocklek, över ett brett spektrum av våglängder från djupa ultravioletta till nära infraröda våglängder (190–1000 nm).

I följande exempel uttrycks notationen för teoretisk och uppmätt reflektans i spektraldiagrammen som "R-teor" respektive "R-mått".

Nedan finns scheman som visar tunnfilmsmätningsprocessen:

Forouhi–Bloomer-spridningsekvationerna i kombination med rigorös kopplad våganalys (RCWA) har också använts för att erhålla detaljerad profilinformation (djup, CD, sidoväggsvinkel) för dikesstrukturer. För att extrahera strukturinformation måste polariserad bredbandsreflektansdata, Rs och Rp , samlas in över ett stort våglängdsområde från en periodisk struktur (gitter), och sedan analyseras med en modell som innehåller Forouhi–Bloomer dispersionsekvationer och RCWA. Indata i modellen inkluderar gitterdelning och n- och k -spektra för alla material i strukturen, medan utdata kan inkludera djup, CD-skivor på flera platser och till och med sidoväggsvinkel. n- och k- spektra för sådana material kan erhållas i enlighet med den metod som beskrivs i detta avsnitt för tunnfilmsmätningar.

Nedan finns scheman som visar mätprocessen för dikeskonstruktioner. Därefter följer exempel på dikesmätningar.

Exempel 1: Amorft kisel på oxiderat kiselsubstrat (a-Si/SiO2 _/ Si-Sub)

Ex. 1: Reflektansspektra samlade över 190–1000 nm våglängdsområde för en amorf kiselfilm (a-Si) på ett oxiderat kiselsubstrat (SiO ₂ /Si-Sub) plus n(λ) och k(λ) -spektra för a- Si film. Filmtjockleken visade sig vara 1147 nm. Tjockleken på a-Si- och Si02- _filmer , plus n(A)- och k(A) -spektra för a-Si bestämdes alla samtidigt. n (X)- och k(X) -spektra för Si02- _filmen hölls fixerade.

Ex. 1: Amorfa material uppvisar typiskt ett brett maximum i sina n(λ)- och k(λ) -spektra. När ett material övergår från det amorfa tillståndet till det helt kristallina tillståndet skärps det breda maximumet upp och andra skarpa toppar börjar dyka upp i n(λ)- och k(λ) -spektra. Detta demonstreras för fallet med amorft kisel som utvecklas till polykisel och vidare till kristallint kisel.

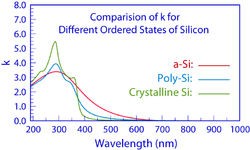
Exempel 1 visar ett brett maximum i n(λ)- och k(λ) -spektra för a-Si-filmen, vilket förväntas för amorfa material. När ett material övergår mot kristallinitet ger det breda maximumet vika för flera skarpare toppar i dess n(λ)- och k(λ) -spektra, vilket visas i grafiken.

När mätningen involverar två eller flera filmer i en bunt filmer måste det teoretiska uttrycket för reflektans utökas till att inkludera n( λ)- och k(λ) -spektra, plus tjocklek, t , för varje film. Regressionen kanske inte konvergerar till unika värden för parametrarna, på grund av den icke-linjära karaktären hos uttrycket för reflektans. Så det är bra att eliminera några av de okända. Till exempel n(λ) - och k(λ) -spektra för en eller flera av filmerna vara kända från litteraturen eller tidigare mätningar, och hållas fixerade (inte tillåtet att variera) under regressionen. För att erhålla resultaten som visas i exempel 1 fixerades n(λ)- och k(λ) -spektra för Si02- _{skiktet , och de andra parametrarna} , n(λ) och k(λ) för a-Si, plus tjocklekar av både a-Si och SiO2 _fick variera.

Exempel 2: 248 nm fotoresist på kiselsubstrat (PR/Si-Sub)

Ex. 2: Reflektansspektra samlade över våglängdsområdet 190–1000 nm för en fotoresistfilm på kiselsubstrat, plus n(λ)- och k(λ) -spektra för fotoresisten. Filmtjockleken visade sig vara 498 nm. Tjockleken och n(A)- och k(A) -spektra för fotoresisten bestämdes alla samtidigt.

Polymerer som fotoresist består av långa kedjor av molekyler som inte bildar en kristallografisk struktur i klassisk mening. Emellertid uppvisar deras n(λ) - och k(λ) -spektra flera skarpa toppar snarare än ett brett maximum som förväntas för icke-kristallina material. Således baseras mätresultaten för en polymer på Forouhi–Bloomer-formuleringen för kristallina material. Det mesta av strukturen i n(λ) - och k(λ) -spektra förekommer i det djupa UV-våglängdsområdet och för att korrekt karakterisera en film av detta slag är det nödvändigt att de uppmätta reflektansdata i det djupa UV-området är korrekta.

Figuren visar ett mätexempel på ett fotoresistmaterial (polymer) som används för 248 nm mikrolitografi. Sex termer användes i Forouhi–Bloomer-ekvationerna för kristallina material för att passa data och uppnå resultaten.

Exempel 3: Indiumtennoxid på glassubstrat (ITO/Glass-Sub)

Ex. 3: Reflektans- och transmittansspektra i intervallet 190–1000 nm för ett obelagt glassubstrat. Observera att T = 0 för glassubstratet i DUV, vilket indikerar absorption i detta område av spektrumet. Man har funnit att värdet på k(λ) i det djupa UV-våglängdsområdet är i storleksordningen k = 3x10 ⁻⁴ , och detta lilla värde som inte är noll överensstämmer med T = 0 i det djupa UV-värdet.

Ex. 3: Reflektans- och transmittansspektra i intervallet 190–1000 nm av ITO avsatt på glassubstratet som beskrivs ovan, plus n(λ)- och k(λ) -spektra för ITO-filmen. ITO-tjocklek på 133nm och dess n(λ)- och k(λ) -spektra bestämdes samtidigt genom att anpassa uppmätta reflektans- och transmittansspektra till teoretiska uttryck av dessa storheter med hjälp av Forouhi-Bloomer-ekvationerna.

Indiumtennoxid (ITO) är ett ledande material med den ovanliga egenskapen att det är genomskinligt, så det används ofta inom plattskärmsindustrin. Reflektans- och transmittansmätningar av det obelagda glassubstratet behövdes för att bestämma de tidigare okända n(A)- och k(A) -spektra för glaset. Reflektansen och transmittansen för ITO avsatt på samma glassubstrat mättes sedan samtidigt och analyserades med Forouhi-Bloomer-ekvationerna.

Som förväntat är k(λ) -spektrumet för ITO noll i det synliga våglängdsområdet, eftersom ITO är transparent. Uppförandet av k(λ) -spektrumet för ITO i de nära-infraröda (NIR) och infraröda (IR) våglängdsområdena liknar det för en metall: icke-noll i NIR-området 750–1000 nm (svårt att urskilja i grafik eftersom dess värden är mycket små) och når ett maximalt värde i IR-området (λ>1000 nm). Det genomsnittliga k -värdet för ITO-filmen i NIR- och IR-området är 0,05.

Exempel 4: Multispektral analys av germanium (40 %)–selen (60 %) tunna filmer

Ex. 4: Multispektral analys användes för att analysera reflektansspektra för en Ge ₄₀ Se ₆₀ -film avsatt på två olika substrat: både kisel och oxiderade kiselsubstrat. Mätningarna gav ett enda n(A)- och k (A) -spektra _{av Ge40Se60} . En tjocklek av 33,6 nm för Ge ₄₀ Se ₆₀ på det oxiderade kiselsubstratet hittades, medan en tjocklek av 34,5 nm av Ge ₄₀ Se ₆₀ på kiselsubstratet hittades. Dessutom bestämdes tjockleken på oxidskiktet till 166 nm.

När man hanterar komplexa filmer kan parametrarna i vissa fall inte lösas unikt. För att begränsa lösningen till en uppsättning unika värden kan en teknik som involverar multispektral analys användas. I det enklaste fallet innebär detta att filmen deponeras på två olika substrat och sedan analyseras resultaten samtidigt med Forouhi–Bloomer dispersionsekvationer.

Till exempel ger den enstaka mätningen av reflektans i området 190–1000 nm för Ge ₄₀ Se ₆₀ /Si inte unika n(λ)- och k(λ) -spektra för filmen. Detta problem kan dock lösas genom att deponera samma Ge ₄₀ Se _60- film på ett annat substrat, i detta fall oxiderat kisel, och sedan samtidigt analysera de uppmätta reflektansdata för att bestämma:

• Tjockleken på Ge ₄₀ Se ₆₀ /Si-filmen på kiselsubstratet som 34,5 nm,
• Tjockleken på Ge ₄₀ Se ₆₀ /Si-filmen på det oxiderade kiselsubstratet som 33,6 nm,
• Tjockleken på SiO2 ₍ med n- och k -spektra för SiO2 _hållna fixerade), och
• n- och k -spektra , i intervallet 190–1000 nm, av Ge40Se60 _{/ Si} .

Exempel 5: Komplex dikesstruktur

Ex. 5: En dikesstruktur bestående av olika filmer och komplex profil. Poly-Si-filmen mättes på ett täckområde av provet och dess n- och k -spektra bestämdes baserat på Forouhi-Bloomer-dispersionsekvationerna. En fast tabell med värden för n- och k -spektra för Si02- _och Si3N4 _{- filmerna} användes . Med n- och k- spektra för dessa filmer till hands och med rigorös kopplad våganalys (RCWA), bestäms sedan filmtjocklekar, olika djup (höjder) inuti diket och CD-skivor.

Ex. 5: Uppmätt Rs- och Rp- reflektans uppsamlade på den komplexa trenchstrukturen.

Trenchstrukturen som avbildas i det intilliggande diagrammet upprepar sig i 160 nm-intervaller, det vill säga den har en given stigning på 160 nm. Graven är sammansatt av följande material:

• M1 _{: Si3N4} _
• M2: Poly-Si
• M3: Sidoväggsoxid (SiO ₂ )
• M4: SiO ₂
• M5 _{: Si3N4} _
• M6: SiO ₂
• M7: Si Substrat
• M8: Luft

Noggranna n- och k -värden för dessa material är nödvändiga för att analysera strukturen. Ofta finns en filtyta på dikeprovet med filmen av intresse för mätningen. I det här exemplet mättes reflektansspektrumet för polykislet på ett täckområde som innehöll polykislet, från vilket dess n- och k -spektra bestämdes i enlighet med den metod som beskrivs i den här artikeln som använder Forouhi-Bloomer-dispersionsekvationerna . Fasta tabeller med n- och k -värden användes för SiO _2- och Si _{3N 4} -filmerna .

Genom att kombinera filmernas n- och k- spektra med Rigorous Coupled-Wave Analysis (RCWA) bestämdes följande kritiska parametrar (även med uppmätta resultat):

	Uppmätt parameter	Resultat
1	Si Djup	27,4 nm
2	CD @ Top of Si	26,4 nm
3	SiO 2 liner bredd	40,2 nm
4	Si 3 N 4 Höjd	28 nm
3	Poly-Si-bredd	92,6 nm
3	Poly-Si höjd	85,6 nm