Booleska Pythagoras trippelproblem

Det booleska pytagoreiska trippelproblemet är ett problem från Ramsey-teorin om huruvida de positiva heltal kan färgas rött och blått så att inga pytagoreiska trippel består av alla röda eller alla blå medlemmar. Problemet med det booleska pythagoreiska trippelproblemet löstes av Marijn Heule , Oliver Kullmann och Victor W. Marek i maj 2016 genom ett datorassisterat bevis .

Påstående

Problemet frågar om det är möjligt att färga vart och ett av de positiva heltal antingen rött eller blått, så att ingen pythagorisk trippel av heltal a , b , c , som uppfyller $a^{2}+ b^{2}=c^{2}$ har alla samma färg.

Till exempel, i Pythagoras trippel 3, 4 och 5 ( ${\displaystyle 3^{2}+4^{2}=5^{2}} )$ , om 3 och 4 är färgade röd, då måste 5 färgas blå.

Lösning

Marijn Heule , Oliver Kullmann och Victor W. Marek visade att en sådan färgning endast är möjlig upp till siffran 7824. Det faktiska uttalandet av satsen som bevisats är

Teorem — Mängden {1, . . . , 7824} kan delas upp i två delar, så att ingen del innehåller en pytagoreisk trippel, medan detta är omöjligt för {1, . . . , 7825}.

Det finns 2 ⁷⁸²⁵ ≈ 3,63×10 ²³⁵⁵ möjliga färgkombinationer för siffrorna upp till 7825 . Dessa möjliga färger reducerades logiskt och algoritmiskt till omkring en biljon (fortfarande mycket komplexa) fall, och de undersöktes med en boolesk tillfredsställelselösare . Att skapa beviset tog cirka 4 CPU-år av beräkning under en period av två dagar på Stampede-superdatorn vid Texas Advanced Computing Center och genererade ett 200 terabyte propositionsbevis, som komprimerades till 68 gigabyte.

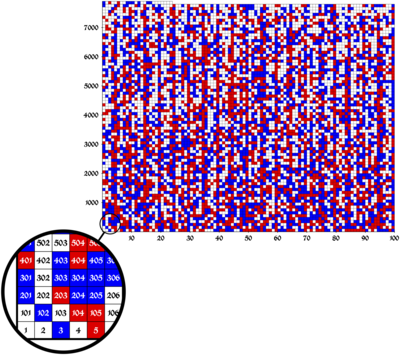
Uppsatsen som beskriver beviset publicerades på SAT 2016-konferensen, där den vann priset för bästa papper. Bilden nedan visar en möjlig färgfamilj för uppsättningen {1,...,7824} utan monokromatisk pytagoreisk trippel, och de vita rutorna kan färgas antingen röda eller blå medan de fortfarande uppfyller detta villkor.

Pris

På 1980-talet erbjöd Ronald Graham ett pris på $100 för lösningen av problemet, som nu har tilldelats Marijn Heule .

Generaliseringar

Från och med 2018 är problemet fortfarande öppet för mer än 2 färger, det vill säga om det finns en k -färgning ( k ≥ 3) av de positiva heltal så att inga pytagoreiska trippel har samma färg.

Se även

Lista över långa matematiska bevis

^ ^a ^b Lamb, Evelyn (26 maj 2016). "Mattebeviset på tvåhundra terabyte är det största någonsin" . Naturen . 534 (7605): 17–18. Bibcode : 2016Natur.534...17L . doi : 10.1038/nature.2016.19990 . PMID 27251254 .
^ ^a ^b Heule, Marijn JH; Kullmann, Oliver; Marek, Victor W. (2016). "Lösa och verifiera problemet med booleska Pythagorean Triples via Cube-and-Conquer". I Creignou, Nadia; Le Berre, Daniel (red.). Teori och tillämpningar av tillfredsställelsetestning – SAT 2016: 19:e internationella konferensen, Bordeaux, Frankrike, 5-8 juli 2016, Proceedings . Föreläsningsanteckningar i datavetenskap. Vol. 9710. s. 228–245. arXiv : 1605.00723 . doi : 10.1007/978-3-319-40970-2_15 .
^ LÖR 2016
^ Eliahou, Shalom; Fromentin, Jean; Marion-Poty, Virginie; Robilliard, Denis (2018-10-02). "Är monokromatiska pytagoreiska trippel oundvikliga under morfiska färger?" . Experimentell matematik . 27 (4): 419–425. arXiv : 1605.00859 . doi : 10.1080/10586458.2017.1306465 . ISSN 1058-6458 . S2CID 19035265 .

[nature-1] Lamb, Evelyn (26 maj 2016). "Mattebeviset på tvåhundra terabyte är det största någonsin" . Naturen . 534 (7605): 17–18. Bibcode : 2016Natur.534...17L . doi : 10.1038/nature.2016.19990 . PMID 27251254 .

[arXiv-2] Heule, Marijn JH; Kullmann, Oliver; Marek, Victor W. (2016). "Lösa och verifiera problemet med booleska Pythagorean Triples via Cube-and-Conquer". I Creignou, Nadia; Le Berre, Daniel (red.). Teori och tillämpningar av tillfredsställelsetestning – SAT 2016: 19:e internationella konferensen, Bordeaux, Frankrike, 5-8 juli 2016, Proceedings . Föreläsningsanteckningar i datavetenskap. Vol. 9710. s. 228–245. arXiv : 1605.00723 . doi : 10.1007/978-3-319-40970-2_15 .

[3] LÖR 2016

[4] Eliahou, Shalom; Fromentin, Jean; Marion-Poty, Virginie; Robilliard, Denis (2018-10-02). "Är monokromatiska pytagoreiska trippel oundvikliga under morfiska färger?" . Experimentell matematik . 27 (4): 419–425. arXiv : 1605.00859 . doi : 10.1080/10586458.2017.1306465 . ISSN 1058-6458 . S2CID 19035265 .