Widlar nuvarande källa

Diagram från Widlars ursprungliga patent

En Widlar-strömkälla är en modifiering av den grundläggande tvåtransistorströmspegeln som innehåller ett emitterdegenerationsmotstånd för endast utgångstransistorn , vilket gör att strömkällan kan generera låga strömmar med endast måttliga motståndsvärden.

Widlar-kretsen kan användas med bipolära transistorer , MOS-transistorer och till och med vakuumrör . Ett exempel på applikation är operationsförstärkaren 741 , och Widlar använde kretsen som en del i många konstruktioner.

Denna krets är uppkallad efter sin uppfinnare, Bob Widlar , och patenterades 1967.

DC-analys

Figur 1: En version av Widlar-strömkällan som använder bipolära transistorer.

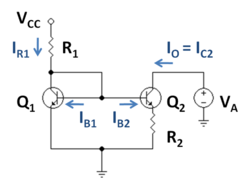
Figur 1 är ett exempel på en Widlar-strömkälla som använder bipolära transistorer, där emittermotståndet R2 _är anslutet till utgångstransistorn Q2 _och har effekten att minska strömmen i _Q2 relativt _Qi . Nyckeln till denna krets är att spänningsfallet över motståndet R2 subtraherar från _bas -emitterspänningen hos transistorn Q2 , och därigenom stänger denna transistor av jämfört med _transistorn Qi _. Denna observation uttrycks genom att likställa basspänningsuttrycken som finns på vardera sidan av kretsen i figur 1 som:

${\begin{aligned}&V_{B}=V_{BE1}=V_{BE2}+(\beta _{2}+1)I_{B2}R_{2}\\\Rightarrow {}&{ \frac {1}{R_{2}}}\left(V_{BE1}-V_{BE2}\right)=(\beta _{2}+1)I_{B2}\ ,\end{aligned}}$

där β ₂ är betavärdet för utgångstransistorn, vilket inte är detsamma som ingångstransistorns, delvis på grund av att strömmarna i de två transistorerna är mycket olika. Variabeln I _B2 är utgångstransistorns basström, VBE avser bas-emitterspänning _. Denna ekvation innebär (med Shockley-diodekvationen ):

Ekv. 1

${\begin{aligned}(\beta _ {2}+1)I_{B2}&=\left(1+{\frac {1}{\beta _{2}}}\right)I_{C2}={\frac {1}{R_{2 }}}\left(V_{BE1}-V_{BE2}\right)\\&={\frac {V_{\text{T}}}{R_{2}}}\left[\ln \left( I_{C1}/I_{S1}\right)-\ln \left(I_{C2}/I_{S2}\right)\right]={\frac {V_{\text{T}}}{R_{ 2}}}\ln \left({\frac {I_{C1}I_{S2}}{I_{C2}I_{S1}}}\right)\ ,\end{aligned}}$

där V _T är den termiska spänningen .

Denna ekvation gör approximationen att strömmarna båda är mycket större än skalströmmarna , I _S1 och I _S2 ; en uppskattning som gäller utom för nuvarande nivåer nära avstängda . I det följande antas skalströmmarna vara identiska; i praktiken måste detta ordnas särskilt.

Konstruktionsprocedur med specificerade strömmar

För att designa spegeln måste utströmmen relateras till de två motståndsvärdena R ₁ och R ₂ . En grundläggande observation är att utgångstransistorn är i aktivt läge endast så länge som dess kollektor-basspänning är icke-noll. _{Sålunda sätter det} enklaste förspänningsvillkoret för utformning av spegeln den pålagda spänningen VA till lika med basspänningen VB . Detta minsta användbara värde på _VA kallas strömkällans överensstämmelsespänning . Med det bias-villkoret spelar den tidiga effekten ingen roll i designen.

Dessa överväganden föreslår följande designprocedur:

• Välj önskad utström, I _O = I _C2 .
• Välj referensströmmen, I _R1 , som antas vara större än utströmmen, förmodligen betydligt större (det är syftet med kretsen).
• Bestäm ingångskollektorströmmen för Q ₁ , I _C1 :

$I_{C1}={\frac {\beta _{1}}{\beta _{1}+1}}\left(I_{R1}-{\frac {I_{C2}}{\beta _{2}}}\right)\ .$

• Bestäm basspänningen V _BE1 med hjälp av diodlag

$V_{BE1}=V_{\text{T}}\ln \left({\frac {I_{C1}}{I_{S}}}\right)=V_{A}\ .$

där jag _S är en enhetsparameter som ibland kallas skalström . Värdet

_{på basspänningen} ställer också in överensstämmelsespänningen VA = _VBE1 . Denna spänning är den lägsta spänningen för vilken spegeln fungerar korrekt.

• Bestäm R ₁ :

$R_{1}={\frac {V_{CC}-V_{A}}{I_{R1}}}\ .$

• Bestäm emitterbensmotståndet R ₂ med Ekv. 1 (för att reducera clutter väljs skalströmmarna lika):

$R_{2}={\frac {V_{\text{T}}}{\left(1+{\frac {1}{\beta _{2}}}\right)I_{C2}} }\ln \left({\frac {I_{C1}}{I_{C2}}}\höger)\ .$

Hitta strömmen med givna motståndsvärden

Det omvända till designproblemet är att hitta strömmen när resistorvärdena är kända. En iterativ metod beskrivs härnäst. Antag att strömkällan är förspänd så att kollektor-basspänningen för utgångstransistorn _Q2 är noll. Strömmen genom R ₁ är ingångs- eller referensströmmen som anges som,

${\ start{aligned}I_{R1}&=I_{C1}+I_{B1}+I_{B2}\\&=I_{C1}+{\frac {I_{C1}}{\beta _{1}} }+{\frac {I_{C2}}{\beta _{2}}}\\&={\frac {1}{R_{1}}}\left(V_{CC}-V_{BE1}\ höger)\end{aligned}}$

Omarrangerande, I _C1 hittas som:

Ekv. 2

$I_{C1}={\frac {\beta _{1}}{\beta _{1}+1}}\left({\frac {V_{CC}-V_{BE1}}{R_{1}}}-{\frac {I_{C2}}{\beta _{2}} }\höger)$

Diod-ekvationen ger:

Ekv. 3

$V_{BE1}=V_{\text{T}}\ln \left({\frac {I_{C1}}{I_{S1}}}\höger)\ .$

Eq.1 ger:

$I_{C2}={\frac {V_{\text{T}}}{\left(1+{\frac {1}{\beta _{2}}}\right)R_{2}} }\ln \left({\frac {I_{C1}}{I_{C2}}}\höger)\ .$

Dessa tre relationer är en olinjär, implicit bestämning av de strömmar som kan lösas genom iteration.

• Vi gissar startvärden för I _C1 och I _C2 .
• Vi hittar ett värde för V _BE1 :

  $V_{BE1}=V_{\text{T}}\ln \left({\frac {I_{C1}}{I_{S1}}}\höger)\ .$

• Vi hittar ett nytt värde för I _C1 :

  $I_{C1}={\frac {\ beta _{1}}{\beta _{1}+1}}\left({\frac {V_{CC}-V_{BE1}}{R_{1}}}-{\frac {I_{C2} }{\beta _{2}}}\right)$

• Vi hittar ett nytt värde för I _C2 :

  $I_{C2}={\frac {V_{\text{T}}}{\left(1+{\frac {1}{\beta _{2}}}\right)R_{2}} }\ln \left({\frac {I_{C1}}{I_{C2}}}\höger)\ .$

Denna procedur upprepas till konvergens och ställs in bekvämt i ett kalkylblad. Man använder helt enkelt ett makro för att kopiera de nya värdena till kalkylbladets celler som innehåller de initiala värdena för att få lösningen på kort tid.

Observera att med kretsen som visas, om V _CC ändras, kommer utströmmen att ändras. För att _hålla utströmmen konstant trots fluktuationer i Vcc bör kretsen därför drivas av en konstant strömkälla snarare än att använda _motståndet R1 .

Exakt lösning

De transcendentala ekvationerna ovan kan lösas exakt i termer av Lambert W-funktionen .

Utgångsimpedans

Figur 2: Småsignalkrets för att hitta utgångsresistans från Widlar-källan som visas i figur 1. En testström _I x _appliceras vid utgången, och utgångsresistansen är då RO = V _x / I _x .

En viktig egenskap hos en strömkälla är dess små inkrementella signalutgångsimpedans, som helst bör vara oändlig. Widlar-kretsen introducerar lokal strömåterkoppling för transistor $\scriptstyle Q_{2}$ . Varje ökning _av strömmen i _Q2 ökar spänningsfallet över R2 , vilket minskar _VBE för Q2 , och _motverkar därigenom ökningen i ström . Denna återkoppling innebär att kretsens utimpedans ökar, eftersom återkopplingen som involverar R2 tvingar användningen av en högre spänning för att driva en given ström _.

Utgångsresistans hittas med hjälp av en liten signalmodell för kretsen, som visas i figur 2. Transistorn Q ₁ ersätts av dess småsignalemitterresistans r _E eftersom den är diodansluten. Transistor Q ₂ ersätts med sin hybrid-pi-modell . En testström I _x är ansluten till utgången.

Med hjälp av figuren bestäms utgångsresistansen med hjälp av Kirchhoffs lagar. Genom att använda Kirchhoffs spänningslag från marken till vänster till jordanslutningen av R ₂ :

$I_{b}\left[(R_{1}\parallel r_{E})+r_{\pi }\right]+[I_{x}+I_{b}]R_{2}=0\ .$

Ordna om:

$I_{b}=-I_{x}{\frac {R_{2}}{(R_{1}\parallel r_{E})+r_{\pi }+R_{2}}}\ .$

Med hjälp av Kirchhoffs spänningslag från jordanslutningen av R ₂ till jord för testströmmen:

$V_{x}=I_{x}(R_{2}+r_{O})+I_{ b}(R_{2}-\beta r_{O})\ ,$

eller, som ersätter I _b :

Ekv. 4

  $\displaystyle R_{O}={\frac {V_{x}}{I_$$+\ R_{2}\left[{\frac {(R_{1}\parallel r_{E})+r_{\pi }}{(R_{1}\parallel r_{E})+r_ {\pi }+R_{2}}}\right]\ .$

Enligt Eq. 4 _över den för själva utgångstransistorn (som är _r O ₎ så länge som R2 är tillräckligt stor jämfört med r _π för utgångstransistorn (stora resistanser R2 gör faktorn multiplicera r _O närmar sig värdet (β + 1)). Utgångstransistorn bär en låg ström, vilket gör r _π stor, och ökning av R2 tenderar att minska denna ström ytterligare, vilket orsakar en korrelerad ökning av r _{π .} Därför kan ett mål för R ₂ ≫ r _π vara orealistiskt, och ytterligare diskussion ges nedan . Resistansen R ₁ ∥ r _E är vanligtvis liten eftersom emitterresistansen r _E vanligtvis bara är några få ohm.

Strömberoende av utgångsresistans

Figur 3: Konstruktionsavvägning mellan utgångsresistans och utgångsström. Topppanel: Kretsutgångsresistans R _O vs. DC-utgångsström I _C2 med hjälp av designformeln för ekv. 5 för R2 ; _{_} Mittpanel: Resistans R _O2 i utgångstransistors emitterben; Nedre panel: Återkopplingsfaktor som bidrar till utgångsresistans. Strömmen i referenstransistorn Qi hålls _konstant , varigenom överensstämmelsespänningen fixeras. Plots antar I _C1 = 10 mA, VA = 50 V, V _CC = 5 V, _I S ₌ 10 fA, β _{1, 2} = 100 oberoende av ström.

Strömberoendet av resistanserna r _π och r _O diskuteras i artikeln hybrid-pi model . Det aktuella beroendet av motståndsvärdena är:

$r_{\pi }={\frac {v_{be}}{i_{b}}}{\Bigg |}_{v_ {ce}=0}={\frac {V_{\text{T}}}{I_{\text{B2}}}}=\beta _{2}{\frac {V_{\text{T}} }{I_{\text{C2}}}}\ ,$

och

$r_{O}={\frac {v_{ce}}{i_{c}}}{\Bigg |}_{v_{be}=0}={ \frac {V_{A}}{I_{C2}}}$

är utgångsresistansen på grund av _Early -effekten när VCB = 0 V (enhetsparameter VA är Early-spänningen) _.

Från tidigare i den här artikeln (ställ in skalströmmarna lika för bekvämlighets skull): Ekv. 5

$R_{2}={\frac {V_{\text{T}}}{\left(1+{\frac {1}{\beta _{2}}}\right)I_{C2}} }\ln \left({\frac {I_{C1}}{I_{C2}}}\höger)\ .$

Följaktligen, för det vanliga fallet med liten r _E , och försummar den andra termen i RO med förväntningen att den ledande termen som involverar r _O är mycket större: Ekv _. 6

${\begin{aligned}R_{O}&\approx r_{O}\left(1+{\frac {\beta _{2}R_{2}}{r_{\pi }+R_ {2}}}\right)\\&=r_{O}\left(1+{\frac {\beta _{2}\ln \left({\frac {I_{C1}}{I_{C2} }}\right)}{\beta _{2}+1+\ln \left({\frac {I_{C1}}{I_{C2}}}\right)}}\right)\end{aligned} }$

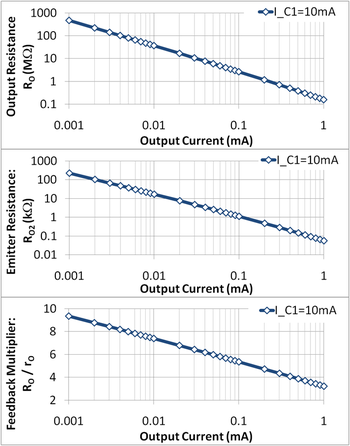
där den sista formen hittas genom att ersätta ekv. 5 för R2 . _{_} Ekv. 6 visar att ett värde på utgångsresistans mycket större än rO för utgångstransistorn endast resulterar i konstruktioner med I _C1 >> I _{C2 .} Figur 3 visar att kretsens utgångsresistans RO inte bestäms så mycket av återkoppling som av strömberoendet av utgångstransistorns resistans rO (utgångsresistansen i figur 3 varierar fyra storleksordningar, medan återkopplingsfaktorn _{endast varierar} med en storleksordning).

Ökning av I _C1 för att öka återkopplingsfaktorn resulterar också i ökad överensstämmelsespänning, inte bra eftersom det betyder att strömkällan fungerar över ett mer begränsat spänningsområde. Så, till exempel, med ett mål för överensstämmelsespänningsinställning, att placera en övre gräns på ICl , och med _{ett mål för att utgångsresistansen ska uppfyllas, är det maximala} värdet för utströmmen IC2 begränsat.

Mittpanelen i figur 3 visar designavvägningen mellan emitterbensresistans och utgångsströmmen: en lägre utström kräver ett större benmotstånd, och därmed en större area för konstruktionen. En övre gräns för arean sätter därför en nedre gräns för utströmmen och en övre gräns för kretsens utgångsresistans.

Ekv. 6 för RO beror på val av ett värde _på R2 enligt ekv _. 5 . Det betyder ekv. 6 är inte en kretsbeteendeformel , utan en designvärdekvation . När R2 väl har valts för ett speciellt designmål med användning av _ekv . 5 , därefter är dess värde fast. Om kretsdrift gör att strömmar, spänningar eller temperaturer avviker från de avsedda värdena; sedan för att förutsäga förändringar i R _O orsakade av sådana avvikelser, Ekv. 4 ska användas, inte ekv. 6 .

Se även

• Nuvarande källa
• Nuvarande spegel
• Wilson nuvarande källa

Vidare läsning

•   Linden T. Harrison (2005). Strömkällor och spänningsreferenser: En designreferens för elektronikingenjörer . Elsevier-Newnes. ISBN 0-7506-7752-X .
•   Sundaram Natarajan (2005). Mikroelektronik: Analys och design . Tata McGraw-Hill. sid. 319. ISBN 0-07-059096-6 .
• Aktuella speglar och aktiva laster: Mu-Huo Cheng