Viterbi dekoder

En Viterbi-avkodare använder Viterbi-algoritmen för att avkoda en bitström som har kodats med hjälp av en faltningskod eller trelliskod .

Det finns andra algoritmer för att avkoda en faltningskodad ström (till exempel Fano-algoritmen) . Viterbi-algoritmen är den mest resurskrävande, men den gör maximal sannolikhetsavkodning . Det används oftast för att avkoda faltningskoder med begränsningslängder k≤3, men värden upp till k=15 används i praktiken.

Viterbi-avkodning utvecklades av Andrew J. Viterbi och publicerades i tidningen Viterbi, A. (april 1967). "Felgränser för faltningskoder och en asymptotiskt optimal avkodningsalgoritm". IEEE-transaktioner på informationsteori . 13 (2): 260–269. doi : 10.1109/tit.1967.1054010 .

Det finns både hårdvara (i modem) och mjukvaruimplementationer av en Viterbi-avkodare.

Viterbi-avkodning används i den iterativa Viterbi-avkodningsalgoritmen .

Implementering av hårdvara

Ett vanligt sätt att implementera en hårdvaruviterbi-avkodare

En hårdvaru-Viterbi-avkodare för grundläggande (ej punkterad) kod består vanligtvis av följande huvudblock:

• Branch metrisk enhet (BMU)
• Path metric unit (PMU)
• Spårningsenhet (TBU)

Branch metrisk enhet (BMU)

Ett exempel på implementering av en grenmetrisk enhet

En grenmetrik enhets funktion är att beräkna grenmetrik , som är normerade avstånd mellan varje möjlig symbol i kodalfabetet och den mottagna symbolen.

Det finns Viterbi-avkodare för hårda beslut och mjuka beslut. En Viterbi-avkodare för svårt beslut får en enkel bitström på sin ingång, och ett Hamming-avstånd används som ett mått. En Viterbi-avkodare för mjukt beslut tar emot en bitström som innehåller information om tillförlitligheten för varje mottagen symbol. Till exempel, i en 3-bitars kodning, kan denna tillförlitlighetsinformation kodas enligt följande:

värde	menande
000	starkast	0
001	relativt stark	0
010	relativt svag	0
011	svagast	0
100	svagast	1
101	relativt svag	1
110	relativt stark	1
111	starkast	1

Naturligtvis är det inte det enda sättet att koda tillförlitlighetsdata.

Det kvadratiska euklidiska avståndet används som ett mått för mjuka beslutsavkodare.

Path metric unit (PMU)

Ett exempel på implementering av en vägmetrisk enhet för en specifik K=4-avkodare

En sökvägsmetrisk enhet sammanfattar förgreningsmått för att få mätvärden för $2^{K-1}$ vägar, där K är kodens begränsningslängd, varav en så småningom kan väljas som optimal . Varje klocka tar den $2^{K-1}$ beslut, vilket avvisar medvetet ooptimala vägar. Resultaten av dessa beslut skrivs till minnet av en spårningsenhet.

Kärnelementen i en PMU är ACS- enheter (Add-Compare-Select) . Sättet på vilket de är kopplade mellan sig definieras av en specifik kods trellisdiagram .

Eftersom grenmått alltid är $\geq 0$ måste det finnas en extra krets (visas inte på bilden) som förhindrar att metriska räknare rinner över. En alternativ metod som eliminerar behovet av att övervaka banans måtttillväxt är att låta banmätningarna "rulla över"; för att använda den här metoden är det nödvändigt att se till att banmetriska ackumulatorer innehåller tillräckligt med bitar för att förhindra att de "bästa" och "sämsta" värdena kommer inom 2 (n-1) ^från varandra. Jämförelsekretsen är väsentligen oförändrad.

Ett exempel på implementering av en ACS-enhet

Det är möjligt att övervaka brusnivån på den inkommande bitströmmen genom att övervaka tillväxthastigheten för det "bästa" vägmåttet. Ett enklare sätt att göra detta är att övervaka en enda plats eller "tillstånd" och se den passera "uppåt" genom säg fyra diskreta nivåer inom ackumulatorns räckvidd. När den passerar uppåt genom var och en av dessa tröskelvärden, inkrementeras en räknare som reflekterar "bruset" som finns på den inkommande signalen.

Spårningsenhet (TBU)

Ett exempel på implementering av en spårningsenhet

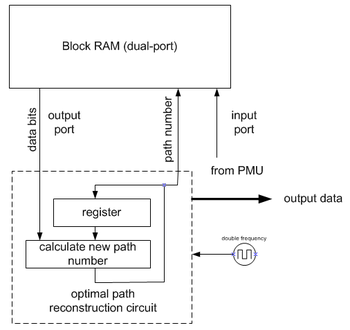
Back-trace-enhet återställer en (nästan) maximal sannolikhetsväg från de beslut som PMU tagit. Eftersom den gör det i omvänd riktning, innefattar en viterbi-avkodare en FILO-buffert (först-in-sist-ut) för att rekonstruera en korrekt ordning.

Observera att implementeringen som visas på bilden kräver dubbel frekvens. Det finns några knep som eliminerar detta krav.

Implementeringsfrågor

Kvantisering för mjuk beslutsavkodning

För att fullt ut utnyttja fördelarna med mjuk beslutsavkodning måste man kvantisera insignalen ordentligt. Den optimala kvantiseringszonens bredd definieras av följande formel:

$\,\!T={\sqrt {\frac {N_{0}}{2^{k}}}},$

där $N_{0}$ är en bruseffektspektraldensitet och k är ett antal bitar för mjukt beslut.

Euklidisk metrisk beräkning

Det kvadratiska normavståndet ( $\ell _{2}$ ) mellan de mottagna och de faktiska symbolerna i kodalfabetet kan förenklas ytterligare till en linjär summa/differensform, vilket gör det mindre beräkningsintensivt.

0 Betrakta en 1/2 faltningskod , som genererar 2 bitar ( 00 , 01 , 10 eller 11 ) för varje ingångsbit ( 1 eller ). Dessa Return-to-Zero- signaler översätts till en Non-Return-to-Zero- form som visas bredvid.

kodalfabetet	vektorkartläggning
00	+1, +1
01	+1, −1
10	−1, +1
11	−1, −1

₀₀ Varje mottagen symbol kan representeras i vektorform som vr _{ vr ₌ r , ri _} , där r och r1 _är mjuka beslutsvärden, vars magnituder anger den mottagna vektorns gemensamma tillförlitlighet , .

Varje symbol i kodalfabetet kan på samma sätt representeras av vektorn vi _. = {±1, ±1}

Den faktiska beräkningen av det euklidiska avståndsmåttet är:

$\,\!D=({\överhögerpil {v_{r}}} -{\overrightarrow {v_{i}}})^{2}={\overrightarrow {v_{r}}}^{2}-2{\overrightarrow {v_{r}}}{\overrightarrow {v_{i }}}+{\overrightarrow {v_{i}}}^{2}$

Varje kvadratterm är ett normerat avstånd, som visar symbolens energi . Till exempel kan energin för symbolen vi ₌ {±1, ±1} beräknas som

$\,\!{\overrightarrow {v_{i}}}^{2}=(\pm 1)^{2}+ (\pm 1)^{2}=2$

Energitermen för alla symboler i kodalfabetet är alltså konstant (vid ( normaliserat ) värde 2).

Operationen Add-Compare-Select ( ACS ) jämför det metriska avståndet mellan den mottagna symbolen ||v _r || och alla 2 symboler i kodalfabetet vars vägar sammanfogas vid en nod i motsvarande trellis, ||v _i ⁽⁰⁾ || och ||v _i ⁽¹⁾ || . Detta motsvarar att jämföra

$\,\!D_{0}={\overrightarrow {v_{r}}}^{2}-2{\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{0}}}+{\overrightarrow {v_{i}^{0}}}^{2}$

och

$\,\!D_{1}={\overrightarrow {v_{r}}}^{2}-2 {\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{1}}}+{\overrightarrow {v_{i}^{1}}}^{2}$

Men från ovan vet vi att energin för v _i är konstant (lika med (normaliserat) värde på 2), och energin för v r _är densamma i båda fallen. Detta minskar jämförelsen till en minimafunktion mellan produkttermerna med två (mitten) prickar ,

$\,\!\min(- 2{\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{0}}},-2{\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{1} }})=\max({\overrightarrow {v_{r}}}{\overrightarrow {v_{i}^{0}}},{\overrightarrow {v_{r}}}{\overrightarrow {v_{i} ^{1}}})$

eftersom en min operation på negativa tal kan tolkas som en ekvivalent maxoperation på positiva storheter.

Varje punktproduktterm kan utökas som

$\,\!\max(\pm r_{0}\pm r_{1},\pm r_{0}\pm r_{1})$

där tecknen för varje term beror på att symbolerna v _i ⁽⁰⁾ och v _i ⁽¹⁾ jämförs. Således kan den kvadratiska euklidiska metriska avståndsberäkningen för att beräkna grenmåttet utföras med en enkel addera/subtrahera operation.

Spåra tillbaka

Det allmänna tillvägagångssättet för spårning är att ackumulera vägmått för upp till fem gånger begränsningslängden (5 ( K - 1)), hitta noden med den största ackumulerade kostnaden och börja spåra från denna nod.

Den vanligen använda tumregeln för ett trunkeringsdjup på fem gånger minnet (begränsningslängd K -1) för en faltningskod är korrekt endast för hastighet 1/2-koder. För en godtycklig hastighet är en korrekt tumregel 2,5( K - 1)/(1− r ) där r är kodhastigheten.

Att beräkna den nod som har ackumulerat den största kostnaden (antingen den största eller minsta integrerade vägmåttet) involverar dock att hitta maxima eller minima för flera (vanligtvis 2 ^{K -1} ) tal, vilket kan vara tidskrävande när det implementeras på inbäddade hårdvarusystem.

De flesta kommunikationssystem använder Viterbi-avkodning som involverar datapaket av fasta storlekar, med ett fast bit / byte -mönster antingen i början eller/och i slutet av datapaketet. Genom att använda det kända bit / byte -mönstret som referens kan startnoden sättas till ett fast värde, varigenom en perfekt maximal sannolikhetsväg erhålls under spårning.

Begränsningar

En fysisk implementering av en viterbi-avkodare kommer inte att ge en exakt maximal sannolikhetsström på grund av kvantisering av insignalen, gren- och vägmått och ändlig spårningslängd . Praktiska implementeringar närmar sig inom 1 dB från det ideala.

Utsignalen från en Viterbi-avkodare, vid avkodning av ett meddelande som skadats av en additiv gaussisk kanal, har fel grupperade i felskurar. Enfelskorrigerande koder kan inte ensamma korrigera sådana skurar, så antingen måste faltningskoden och Viterbi-avkodaren vara tillräckligt kraftfulla för att driva ner fel till en acceptabel hastighet, eller så måste skurfelkorrigerande koder användas.

Punkterade koder

En hårdvaruviterbi-avkodare för punkterade koder implementeras vanligtvis på ett sådant sätt:

• En depunkterare, som omvandlar ingångsströmmen till strömmen som ser ut som en original (icke punkterad) ström med ERASE-märken på de platser där bitar raderades.
• En grundläggande viterbi-avkodare som förstår dessa ERASE-märken (det vill säga inte använder dem för grenmetrikberäkning).

Mjukvaruimplementering

Huvudartikel: Viterbi-algoritm

En av de mest tidskrävande operationerna är en ACS-fjäril, som vanligtvis implementeras med hjälp av ett assemblerspråk och lämpliga instruktionsuppsättningar (som SSE2 ) för att påskynda avkodningstiden.

Ansökningar

Viterbi-avkodningsalgoritmen används ofta inom följande områden:

• Radiokommunikation: digital-TV ( ATSC , QAM , DVB-T , etc.), radiorelä , satellitkommunikation , PSK31 digitalt läge för amatörradio .
• Avkodning av trelliskodad modulering (TCM), tekniken som används i telefonlinjemodem för att pressa ut hög spektral effektivitet ur analoga telefonlinjer med 3 kHz-bandbredd.
• Datorlagringsenheter som hårddiskar .
• Automatisk taligenkänning

externa länkar

• Forney, G. David, Jr (29 april 2005). "Viterbi-algoritmen: En personlig historia". arXiv : cs/0504020 .
• Detaljer om Viterbi-avkodning, samt en bibliografi .
• Viterbi-algoritmförklaring med fokus på problem med hårdvaruimplementering .
• r =1/6 k =15 kodning för Cassini-uppdraget till Saturnus .
• Online Generator av optimerad mjukvara Viterbi-avkodare (GPL) .
• GPL Viterbi dekoderprogramvara för fyra standardkoder .
• Beskrivning av en k =24 Viterbi-avkodare, som tros vara den största någonsin i praktisk användning .
• Generisk Viterbi-avkodarhårdvara (GPL) .