Konvolutionell kod

Inom telekommunikation är en faltningskod en typ av felkorrigerande kod som genererar paritetssymboler via den glidande tillämpningen av en boolesk polynomfunktion till en dataström. Den glidande applikationen representerar kodarens "faltning" över data, vilket ger upphov till termen "faltningskodning". Den glidande karaktären hos faltningskoderna underlättar spaljéavkodning med användning av en tidsinvariant spaljé. Tidsinvariant spaljéavkodning tillåter faltningskoder att avkodas med högst sannolikhet mjukt beslut med rimlig komplexitet.

Möjligheten att utföra ekonomisk mjukbeslutsavkodning med maximal sannolikhet är en av de största fördelarna med faltningskoder. Detta i motsats till klassiska blockkoder, som vanligtvis representeras av en tidsvariant spaljé och därför vanligtvis avkodas med hårda beslut. Konvolutionskoder kännetecknas ofta av baskodhastigheten och djupet (eller minnet) hos kodaren $[n,k,K]$ . Baskodhastigheten ges typiskt som $n/k$ , där $n$ är den råa indatahastigheten och $k$ är datahastigheten för en utkanalskodad ström. $n$ är mindre än $k$ eftersom kanalkodning infogar redundans i ingångsbitarna. Minnet kallas ofta för "begränsningslängden" $K$ , där utgången är en funktion av den aktuella ingången såväl som de tidigare $K-1$ -ingångarna. Djupet kan också anges som antalet minneselement $v$ i polynomet eller det maximalt möjliga antalet tillstånd för kodaren (typiskt: ${\displaystyle 2^{v}} )$ .

Konvolutionskoder beskrivs ofta som kontinuerliga. Det kan emellertid också sägas att faltningskoder har godtycklig blocklängd, snarare än att vara kontinuerlig, eftersom de flesta faltningskoder i verkligheten utförs på datablock. Konvolutionskodade blockkoder använder typiskt terminering. Den godtyckliga blocklängden för faltningskoder kan också jämföras med klassiska blockkoder , som i allmänhet har fasta blocklängder som bestäms av algebraiska egenskaper.

Kodhastigheten för en faltningskod modifieras vanligtvis via symbolpunktering . Till exempel kan en faltningskod med en 'moder' kodhastighet $n/k=1/2$ punkteras till en högre frekvens på till exempel $7 /8$ helt enkelt genom att inte sända en del av kodsymboler. Prestandan hos en punkterad faltningskod skalar i allmänhet bra med mängden paritet som överförs. Möjligheten att utföra ekonomisk mjuk beslutsavkodning på faltningskoder, såväl som blocklängden och kodhastighetsflexibiliteten för faltningskoder, gör dem mycket populära för digital kommunikation.

Historia

Konvolutionskoder introducerades 1955 av Peter Elias . Man trodde att faltningskoder kunde avkodas med godtycklig kvalitet på bekostnad av beräkning och fördröjning. 1967 Andrew Viterbi att faltningskoder kunde avkodas med maximal sannolikhet med rimlig komplexitet med hjälp av tidsinvarianta trellisbaserade avkodare - Viterbi-algoritmen . Andra trellisbaserade avkodaralgoritmer utvecklades senare, inklusive BCJR- avkodningsalgoritmen.

Rekursiva systematiska faltningskoder uppfanns av Claude Berrou omkring 1991. Dessa koder visade sig vara särskilt användbara för iterativ bearbetning inklusive bearbetning av sammanlänkade koder såsom turbokoder .

Med användning av "faltnings"-terminologin kan en klassisk faltningskod betraktas som ett FIR-filter ( Finite Impulse Response) , medan en rekursiv faltningskod kan betraktas som ett Infinite Impulse Response (IIR)-filter.

Där faltningskoder används

Stadier av kanalkodning i GSM. Blockkodare och paritetskontroll - feldetekteringsdel. Konvolutionell kodare och Viterbi-avkodare - felkorrigeringsdel. Interleaving och Deinterleaving - kodordsseparation ökar i tidsdomän och för att undvika bursty förvrängningar.

Konvolutionskoder används i stor utsträckning för att uppnå tillförlitlig dataöverföring i många tillämpningar, såsom digital video , radio, mobilkommunikation (t.ex. i GSM-, GPRS-, EDGE- och 3G-nätverk (tills 3GPP Release 7)) och satellitkommunikation . Dessa koder implementeras ofta i kombination med en hårdbeslutskod, särskilt Reed–Solomon . Före turbokoderna var sådana konstruktioner de mest effektiva och kom närmast Shannon-gränsen .

Konvolutionell kodning

₀₀ För att faltningskoda data, börja med k minnesregister , vart och ett med en ingångsbit. Om inget annat anges börjar alla minnesregister med värdet 0. Kodaren har n modulo-2 adderare (en modulo 2 adderare kan implementeras med en enda boolesk XOR-grind , där logiken är: $0+0 = 0$ , $0+ 1 = 1$ , $1+0 = 1$ , $1+1 = 0$ ), och n generatorpolynom — ett för varje adderare (se figuren nedan). En ingångsbit mi matas till registret längst till vänster _. Genom att använda generatorpolynomen och de existerande värdena i de återstående registren matar kodaren ut n symboler. Dessa symboler kan sändas eller punkteras beroende på önskad kodhastighet. Bitskifta nu alla registervärden åt höger ( m ₁ flyttas till m , m flyttas till m ₋₁ ) och vänta på nästa ingångsbit. Om det inte finns några kvarvarande ingångsbitar, fortsätter kodaren att skifta tills alla register har återgått till nolltillståndet (spolningsbitavslutning).

Bild 1. Rate 1/3 icke-rekursiv, icke-systematisk faltningskodare med begränsningslängd 3

Figuren nedan är en frekvenskodare på 1 ⁄ 3 ( m ⁄ n ) med en begränsningslängd ( k ) på 3. Generatorpolynom är $G 1 = (1,1,1),$ $G 2 = (0,1,1)$ och $. G3 = (1,0,1$ ) Därför beräknas utgångsbitar (modulo 2) enligt följande:

₀ n ₁ = m ₁ + m + m ₋₁

₀ n ₂ = m + m ₋₁

n ₃ = m ₁ + m ₋₁ .

Konvolutionskoder kan vara systematiska och icke-systematiska:

systematisk upprepar meddelandets struktur före kodning
icke-systematiska ändrar den ursprungliga strukturen

Icke-systematiska faltningskoder är mer populära på grund av bättre brusimmunitet. Det hänför sig till faltningskodens fria distans.

En kort illustration av icke-systematisk faltningskod.
En kort illustration av systematisk faltningskod.

Rekursiva och icke-rekursiva koder

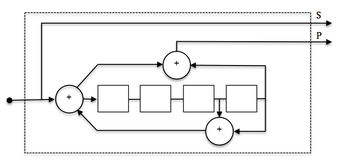
Kodaren på bilden ovan är en icke-rekursiv kodare. Här är ett exempel på en rekursiv och som sådan medger den en återkopplingsstruktur:

Bild 2. Rate 1/2 8-tillstånd rekursiv systematisk faltningskodare. Används som ingående kod i 3GPP 25.212 Turbo Code.

Exempelkodaren är systematisk eftersom indata också används i utgångssymbolerna (utgång 2). Koder med utdatasymboler som inte inkluderar indata kallas icke-systematiska.

Rekursiva koder är vanligtvis systematiska och omvänt är icke-rekursiva koder vanligtvis icke-systematiska. Det är inte ett strikt krav, utan en vanlig praxis.

Exempelkodaren i Img. 2. är en 8-tillståndskodare eftersom de 3 registren kommer att skapa 8 möjliga kodartillstånd (2 ³ ). En motsvarande avkodarspaljé använder vanligtvis 8 tillstånd också.

Rekursiva systematiska faltningskoder (RSC) har blivit mer populära på grund av deras användning i turbokoder. Rekursiva systematiska koder kallas också pseudosystematiska koder.

Andra RSC-koder och exempelapplikationer inkluderar:

Img. 3. Två-tillstånd rekursiv systematisk faltningskod (RSC). Kallas även en "ackumulator".

Användbar för implementering av LDPC- kod och som inre beståndsdelkod för seriella sammanfogade faltningskoder ( SCCC).

Img. 4. Fyra-tillstånd rekursiv systematisk faltningskod (RSC).

Användbar för SCCC:er och flerdimensionella turbokoder.

Img. 5. Sexton-tillstånd rekursiv systematisk faltningskod (RSC).

Användbar som ingående kod i turbokoder med låg felfrekvens för applikationer som satellitlänkar. Även lämplig som SCCC yttre kod.

Impulssvar, överföringsfunktion och begränsningslängd

En faltningskodare kallas så eftersom den utför en faltning av ingångsströmmen med kodarens impulssvar :

y_{i}^{j}=\summa _{k=0}^{\infty }h_{k}^{j}x_{ik}=(x*h^{j})[i],

där $x$ är en ingångssekvens, $y j$ är en sekvens från utgång $j$ , $h j$ är ett impulssvar för utgång $j$ och ${*}$ anger faltning.

En faltningskodare är ett diskret linjärt tidsinvariant system . Varje utsignal från en kodare kan beskrivas med sin egen överföringsfunktion , som är nära relaterad till generatorpolynomet. Ett impulssvar är kopplat till en överföringsfunktion genom Z-transform .

Överföringsfunktioner för den första (icke-rekursiva) kodaren är:

$H_{1}(z)=1+z^{-1}+z^{-2},\,$
$H_{2}(z)=z^{-1}+z^{-2},\,$
$H_{3}(z)=1+z^{-2}.\,$

Överföringsfunktioner för den andra (rekursiva) kodaren är:

$H_{1}(z)={\frac {1+z^{-1}+z ^{-3}}{1-z^{-2}-z^{-3}}},\,$
$H_{2}(z)=1.\,$

Definiera $m$ med

m=\max _{i}\operatörsnamn {polydeg} (H_{i}(1/z))\,

där, för valfri rationell funktion $f(z)=P(z)/Q(z)\,$ ,

\operatorname {polydeg} (f)=\max(\deg(P),\deg(Q))\,

.

Då är $m$ maximum av polynomgraderna för ${\displaystyle H_{i}(1/z)\,} ,$ och begränsningslängden definieras som $K =m+1\,$ . Till exempel, i det första exemplet är begränsningslängden 3, och i det andra är begränsningslängden 4.

Spaljédiagram

En faltningskodare är en finita tillståndsmaskin . En kodare med n binära celler kommer att ha 2 ⁿ tillstånd.

₀ Föreställ dig att kodaren (visas på bild 1 ovan) har '1' i den vänstra minnescellen ( m ), och '0' i den högra ( m ₋₁ ). ( m ₁ är egentligen inte en minnescell eftersom den representerar ett aktuellt värde). Vi kommer att beteckna ett sådant tillstånd som "10". Enligt en ingångsbit kan kodaren vid nästa varv omvandla antingen till "01"-tillståndet eller "11"-tillståndet. Man kan se att inte alla övergångar är möjliga för (t.ex. en avkodare kan inte konvertera från "10"-tillstånd till "00" eller ens stanna i "10"-tillstånd).

Alla möjliga övergångar kan visas enligt nedan:

Bild 6. Ett spaljédiagram för kodaren på bild 1. En stig genom spaljén visas som en röd linje. De heldragna linjerna indikerar övergångar där en "0" matas in och de streckade linjerna där en "1" matas in.

En verklig kodad sekvens kan representeras som en väg på denna graf. En giltig sökväg visas i rött som exempel.

Det här diagrammet ger oss en idé om avkodning : om en mottagen sekvens inte passar denna graf, så togs den emot med fel, och vi måste välja den närmaste korrekta (passar grafen) sekvens. De verkliga avkodningsalgoritmerna utnyttjar denna idé.

Fritt avstånd och felfördelning

Teoretiska bitfelsfrekvenskurvor för kodad QPSK (rekursiv och icke-rekursiv, mjukt beslut), additiv vit Gaussisk bruskanal. Kurvorna är små utmärkande på grund av ungefär samma fria avstånd och vikter.

Det fria avståndet ( d ) är det minimala Hamming-avståndet mellan olika kodade sekvenser. Korrigeringsförmågan ( t ) för en faltningskod är antalet fel som kan korrigeras av koden . Det kan beräknas som

t=\left\lfloor {\frac {d-1}{2}}\right\rfloor .

Eftersom en faltningskod inte använder block, utan bearbetar istället en kontinuerlig bitström, gäller värdet för t en mängd fel som ligger relativt nära varandra. Det vill säga att flera grupper av t- fel vanligtvis kan fixas när de är relativt långt ifrån varandra.

Fritt avstånd kan tolkas som den minimala längden av en felaktig "skur" vid utgången av en faltningsavkodare. Det faktum att fel uppträder som "skurar" bör tas med i beräkningen när man designar en sammanfogad kod med en inre faltningskod. Den populära lösningen för detta problem är att interfoliera data före faltningskodning, så att den yttre blockkoden (vanligtvis Reed–Solomon ) kan korrigera de flesta felen.

Avkodning av faltningskoder

Bitfelförhållandekurvor för faltningskoder med olika alternativ för digitala moduleringar ( QPSK, 8-PSK , 16-QAM, 64-QAM ) och LLR- algoritmer. (Exakt och Ungefärlig) över additiv vit Gaussisk bruskanal.

flera algoritmer för att avkoda faltningskoder. För relativt små värden på k används Viterbi-algoritmen universellt eftersom den ger maximal sannolikhetsprestanda och är mycket parallelliserbar. Viterbi-avkodare är således lätta att implementera i VLSI- hårdvara och i mjukvara på CPU:er med SIMD- instruktionsuppsättningar.

Längre begränsningslängdkoder avkodas mer praktiskt med någon av flera sekventiella avkodningsalgoritmer , av vilka Fano -algoritmen är den mest kända. Till skillnad från Viterbi-avkodning är sekventiell avkodning inte maximal sannolikhet, men dess komplexitet ökar endast något med begränsningslängden, vilket tillåter användning av starka koder med lång begränsningslängd. Sådana koder användes i Pioneer-programmet i början av 1970-talet till Jupiter och Saturnus, men gav plats för kortare, Viterbi-avkodade koder, vanligtvis sammanlänkade med stora Reed-Solomon felkorrigeringskoder som gör den övergripande bitfelshastighetskurvan brantare och producerar extremt låga återstående oupptäckta felfrekvenser.

Både Viterbi och sekventiella avkodningsalgoritmer returnerar svåra beslut: de bitar som bildar det mest sannolika kodordet. Ett ungefärligt konfidensmått kan läggas till varje bit genom att använda algoritmen Soft output Viterbi . Maximala a posteriori (MAP) mjuka beslut för varje bit kan erhållas genom att använda BCJR-algoritmen .

Populära faltningskoder

Skiftregister för (7, [171, 133]) faltningskodpolynomet. Grenar:

h^{1}=171_{o}=[1111001]_{b}

,

h^ {2}=133_{o}=[1011011]_{b}

. Alla matematiska operationer ska göras av modulo 2.

Teoretiska bitfelsfrekvenskurvor för kodad QPSK (mjukt beslut), additiv vit Gaussisk bruskanal. Längre begränsningslängder ger mer kraftfulla koder, men komplexiteten i Viterbi-algoritmen ökar exponentiellt med begränsningslängder, vilket begränsar dessa kraftfullare koder till djupa rymduppdrag där den extra prestandan lätt är värd den ökade avkodarkomplexiteten.

Faktum är att fördefinierade faltningskodstrukturer som erhållits under vetenskaplig forskning används i industrin. Detta hänför sig till möjligheten att välja katastrofala faltningskoder (orsakar ett större antal fel).

En särskilt populär Viterbi-avkodad faltningskod, som används åtminstone eftersom Voyager-programmet har en begränsningslängd $K$ på 7 och en hastighet r på 1/2.

Mars Pathfinder , Mars Exploration Rover och Cassini-sonden till Saturnus använder ett $K$ på 15 och en hastighet på 1/6; denna kod presterar cirka 2 dB bättre än den enklare $K=7$ -koden till en kostnad av 256× i avkodningskomplexitet (jämfört med Voyager-uppdragskoder).

Faltningskoden med en begränsningslängd på 2 och en hastighet på 1/2 används i GSM som en felkorrigeringsteknik.

Punkterade faltningskoder

Konvolutionskoder med 1/2 och 3/4 kodhastigheter (och begränsningslängd 7, mjukt beslut, 4-QAM / QPSK / OQPSK).

Konvolutionskod med valfri kodhastighet kan utformas baserat på polynomval; Men i praktiken används ofta en punkteringsprocedur för att uppnå den erforderliga kodhastigheten. Punktering är en teknik som används för att göra en m / n hastighetskod från en "grundläggande" låghastighetskod (t.ex. 1/ n ). Det uppnås genom att radera vissa bitar i kodarutgången. Bitar raderas enligt en punkteringsmatris . Följande punkteringsmatriser är de mest använda:

Kodpris

Punkteringsmatris

Fritt avstånd (för NASA standard K=7 faltningskod)

1/2 (Ingen perf.)

1

10

2/3

1	0
1	1

6

3/4

1	0	1
1	1	0

5

5/6

1	0	1	0	1
1	1	0	1	0

4

7/8

1	0	0	0	1	0	1
1	1	1	1	0	1	0

3

Om vi till exempel vill skapa en kod med hastigheten 2/3 med hjälp av lämplig matris från tabellen ovan, bör vi ta en grundläggande kodarutgång och sända varje första bit från den första grenen och varje bit från den andra. Den specifika sändningsordningen definieras av respektive kommunikationsstandard.

Punkterade faltningskoder används i stor utsträckning i satellitkommunikation , till exempel i INTELSAT- system och Digital Video Broadcasting .

Punkterade faltningskoder kallas också "perforerade".

Turbokoder: ersätter faltningskoder

En turbokod med komponentkoderna 13, 15. Turbokoder får sitt namn eftersom dekodern använder feedback, som en turbomotor. Permutation betyder detsamma som interfoliering. C1 och C2 är rekursiva faltningskoder. Rekursiva och icke-rekursiva faltningskoder skiljer sig inte så mycket i BER-prestanda, men rekursiv typ av är implementerad i Turbo-faltningskoder på grund av bättre interfolieringsegenskaper.

Enkla Viterbi-avkodade faltningskoder ger nu plats för turbokoder , en ny klass av itererade korta faltningskoder som närmar sig de teoretiska gränserna som Shannons sats medför mycket mindre avkodningskomplexitet än Viterbi-algoritmen för de långa faltningskoderna som skulle krävas för samma prestation. Sammankoppling med en yttre algebraisk kod (t.ex. Reed–Solomon ) tar upp problemet med felgolv som är inneboende i turbokoddesigner.

Se även

Quantum convolutional code

Den här artikeln innehåller material från allmän egendom från Federal Standard 1037C . General Services Administration . Arkiverad från originalet 2022-01-22.

externa länkar

Den on-line läroboken: Information Theory, Inference, and Learning Algorithms , av David JC MacKay , diskuterar faltningskoder i kapitel 48.
Sidan Error Correcting Codes (ECC).
Matlab förklaringar
Fundamentals of Convolutional Decoders for Better Digital Communications
Konvolutionskoder (MIT)
Information Theory and Coding (TU Ilmenau), diskuterar faltningskoder på sidan 48.

Vidare läsning

Publikationer

Francis, Michael. "Viterbi Decoder Block Decoding-Spaljéavslutning och svansbitning." Xilinx XAPP551 v2. 0, DD (2005): 1-21.
Chen, Qingchun, Wai Ho Mow och Pingzhi Fan. "Några nya resultat om rekursiva faltningskoder och deras tillämpningar." Information Theory Workshop, 2006. ITW'06 Chengdu. IEEE. IEEE, 2006.
Fiebig, UC., och Patrick Robertson. "Mjukt besluts- och raderingsavkodning i snabba frekvenshoppningssystem med faltnings-, turbo- och Reed-Solomon-koder." IEEE Transactions on Communications 47.11 (1999): 1646-1654.
Bhaskar, Vidhyacharan och Laurie L. Joiner. "Prestanda av punkterade faltningskoder i asynkron CDMA-kommunikation under perfekta fasspårningsförhållanden." Computers & Electrical Engineering 30.8 (2004): 573-592.
Modestino, J. och Shou Mui. "Konvolutionell kodprestanda i den riciska fadingkanalen." IEEE Transactions on Communications 24.6 (1976): 592-606.
Chen, Yuh-Long och Che-Ho Wei. "Prestandeutvärdering av faltningskoder med MPSK på riciska fadingkanaler." IEE Proceedings F-kommunikation, radar och signalbehandling. Vol. 134. Nr 2. IET, 1987.