Burst felkorrigerande kod

I kodningsteorin använder skurfelkorrigerande koder metoder för att korrigera skurfel , vilket är fel som uppstår i många på varandra följande bitar snarare än att förekomma i bitar oberoende av varandra .

Många koder har utformats för att korrigera slumpmässiga fel . Ibland kan dock kanaler introducera fel som lokaliseras i ett kort intervall. Sådana fel uppstår i en skur (kallade skurfel ) eftersom de inträffar i många på varandra följande bitar. Exempel på burst-fel kan hittas i stor utsträckning i lagringsmedier. Dessa fel kan bero på fysisk skada som repor på en skiva eller ett blixtnedslag i händelse av trådlösa kanaler. De är inte oberoende; de tenderar att vara rumsligt koncentrerade. Om en bit har ett fel är det troligt att de intilliggande bitarna också kan vara skadade. Metoderna som används för att korrigera slumpmässiga fel är ineffektiva för att korrigera skurfel.

Definitioner

En skur av längd 5

En skur av längd ℓ

Säg att ett kodord $C$ sänds och det tas emot som ${\displaystyle Y=C+E.} Sedan$ kallas felvektorn ${\displaystyle E} en skur av längd$$\ell$ om komponenterna som inte är noll i $E$ är begränsade till ${ \displaystyle \ell }$ på varandra följande komponenter. Till exempel är $E=(0{\textbf {1000011}}0)$ en skur med längden $\ell =7.$

Även om denna definition är tillräcklig för att beskriva vad ett skurfel är, förlitar sig majoriteten av de verktyg som utvecklats för skurfelskorrigering på cykliska koder. Detta motiverar vår nästa definition.

En cyklisk skur med längden ℓ

En felvektor $E$ kallas ett cykliskt skurfel med längden $\ell$ om dess komponenter som inte är noll är begränsade till $\ell$ cykliskt på varandra följande komponenter. Till exempel är den tidigare betraktade felvektorn $E=(010000110)$ en cyklisk skur med längden $\ell =5$ , eftersom vi betraktar felet som börjar vid position $6$ och slutar på position $1$ . Lägg märke till att indexen är $0$ -baserade, det vill säga det första elementet är på position $0$ .

I resten av den här artikeln kommer vi att använda termen burst för att referera till en cyklisk burst, om inte annat anges.

Burst beskrivning

Det är ofta användbart att ha en kompakt definition av ett skurfel, som omfattar inte bara dess längd utan också mönstret och platsen för ett sådant fel. Vi definierar en skurbeskrivning som en tupel $(P,L)$ där $P$ är mönstret för felet (det vill säga strängen av symboler som börjar med den första posten som inte är noll i felmönstret och slutar med den sista symbolen som inte är noll), och $L$ är platsen, på kodordet, där skuren kan hittas.

är skurbeskrivningen $D=(1000011,1)$ felmönstret $E=(010000110)$ . Observera att en sådan beskrivning inte är unik, eftersom $D'=(11001,6)$ beskriver samma skurfel. I allmänhet, om antalet komponenter som inte är noll i $E$ är $w$ , så kommer $E$ att ha $w$ olika skurbeskrivningar som var och en börjar med en annan post som inte är noll. $E$ . För att åtgärda de problem som uppstår av tvetydigheten i skurbeskrivningar med satsen nedan, men innan vi gör det behöver vi en definition först.

Definition. Antalet symboler i ett givet felmönster $y,$ betecknas med $\mathrm {längd} (y).$

Sats (Uniqueness of burst descriptions) — Antag att $E$ är en felvektor med längden $n$ med två skurbeskrivningar $(P_{1},L_{1 })$ och $(P_{2},L_{2})$ . Om $\mathrm {length} (P_{1})+\mathrm {length} (P_{ 2})\leqslant n+1,$ då är de två beskrivningarna identiska, det vill säga deras komponenter är ekvivalenta.

Bevis

Låt $w$ vara hammingvikten (eller antalet poster som inte är noll) för $E$ . Då $E$ exakt $w$ felbeskrivningar. För $w=0,1,$ finns det inget att bevisa. Så vi antar att $w\geqslant 2$ och att beskrivningarna inte är identiska. Vi märker att varje post som inte är noll i $E$ kommer att visas i mönstret, och så kommer komponenterna i $E$ som inte ingår i mönstret att bilda en cyklisk serie nollor, som börjar efter den sista posten som inte är noll , och fortsätter precis innan mönstrets första post som inte är noll. Vi kallar den uppsättning index som motsvarar denna körning som nollkörningen. Vi observerar omedelbart att varje skurbeskrivning har en nollkörning associerad med sig och att varje nollkörning är osammanhängande. Eftersom vi har $w$ noll körningar, och var och en är disjunkt, har vi totalt $nw$ distinkta element i alla nollkörningar. Å andra sidan har vi:

$${\begin{aligned}nw={\text{antal nollor i }}E&\geqslant (n-\mathrm {längd} (P_{1}))+(n-\mathrm { length} (P_{2}))\\&=2n-\left(\mathrm {length} (P_{1})+\mathrm {length} (P_{2})\right)\\&\geqslant 2n -(n+1)&&\mathrm {length} (P_{1})+\mathrm {length} (P_{2})\leqslant n+1\\&=n-1\end{aligned}}$$

Detta motsäger $w\geqslant 2.$ Således är skurfelsbeskrivningarna identiska.

En följd av ovanstående sats är att vi inte kan ha två distinkta skurbeskrivningar för skurar med längden ${\tfrac {1}{2}}(n+1).$

Cykliska koder för korrigering av skurfel

Cykliska koder definieras enligt följande: tänk på $q$ -symbolerna som element i $\mathbb {F} _{q}$ . Nu kan vi tänka på ord som polynom över $\mathbb {F} _{q},$ där de individuella symbolerna i ett ord motsvarar polynomets olika koefficienter. För att definiera en cyklisk kod väljer vi ett fast polynom, kallat generatorpolynom . Kodorden för denna cykliska kod är alla polynom som är delbara med detta generatorpolynom.

Kodord är polynom med graden $\leqslant n-1$ . Antag att generatorpolynomet $g(x)$ har graden $r$ . Polynom med graden $\leqslant n-1$ som är delbara med $g(x)$ blir resultatet av att multiplicera $g(x)$ med polynom av grad $\leqslant n-1-r$ . Vi har $q^{nr}$ sådana polynom. Var och en av dem motsvarar ett kodord. Därför är $k=nr$ för cykliska koder.

Cykliska koder kan detektera alla skurar med längd upp till $\ell =nk=r$ . Vi kommer att se senare att skurfelsdetekteringsförmågan för vilken som helst ${\displaystyle (n,k)}-$ kod är avgränsad från ovan av $\ell \leqslant nk$ . Cykliska koder anses vara optimala för skurfelsdetektering eftersom de uppfyller denna övre gräns:

Teorem (Cyklisk skurkorrigeringsförmåga) — Varje cyklisk kod med generatorpolynom av grad $r$ kan detektera alla skurar med längden $\leqslant r.$

Bevis

Vi måste bevisa att om du lägger till en skur med längden $\leqslant r$ till ett kodord (dvs. till ett polynom som är delbart med $g(x)$ ), så blir resultatet kommer inte att vara ett kodord (dvs. motsvarande polynom är inte delbart med $g(x)$ ). Det räcker för att visa att ingen skur av längden $\leqslant r$ är delbar med $g(x)$ . En sådan skur har formen $x^{i}b(x)$ , där $\deg(b(x))<r.$ Därför är $b(x)$ inte delbart med $g(x)$ (eftersom den senare har grad $r$ ). $g(x)$ är inte delbart med $x$ (Annars skulle alla kodord börja med $0$ ). Därför ${\displaystyle x^{i}} inte$ heller delbart med ${\displaystyle g(x)} .$

Ovanstående bevis föreslår en enkel algoritm för skurfelsdetektering/-korrigering i cykliska koder: givet ett sänt ord (dvs ett polynom med graden ${\displaystyle \leqslant n-1} ),$ beräkna resten av detta ord när det delas av $g(x)$ . Om resten är noll (dvs om ordet är delbart med $g(x)$ ), så är det ett giltigt kodord. Rapportera annars ett fel. För att rätta till detta fel, subtrahera denna återstod från det överförda ordet. Subtraktionsresultatet kommer att vara delbart med $g(x)$ (dvs det kommer att vara ett giltigt kodord).

Genom den övre gränsen för skurfelsdetektering ( $\ell \leqslant nk=r$ ), vet vi att en cyklisk kod inte kan detektera alla skurar med längd $\ell >r$ . Men cykliska koder kan verkligen detektera de flesta skurar av längd $>r$ . Anledningen är att detektionen misslyckas endast när skuren är delbar med $g(x)$ . Över binära alfabet finns det $2^{\ell -2}$ skurar med längd $\ell$ . Av dessa är endast $2^{\ell -2-r}$ delbara med $g(x)$ . Därför är sannolikheten för detektionsfel mycket liten ( $2^{-r}$ ) om man antar en enhetlig fördelning över alla skurar av längd $\ell$ .

Vi överväger nu ett grundläggande teorem om cykliska koder som kommer att hjälpa till att designa effektiva skurfelskorrigerande koder, genom att kategorisera skurar i olika coset.

Teorem (Distinct Cosets ) — En linjär kod $C$ är en $\ell$ -burst-felkorrigerande kod om alla burst-fel av längd $\leqslant \ell$ ligger i distinkta coset av $C$ .

Bevis

Låt $\mathbf {e} _{1},\mathbf {e} _{2}$ vara distinkta burst-fel av längd $\leqslant \ell$ som ligger i samma coset av kod $C$ . Då $\mathbf {c} =\mathbf {e} _{1}-\mathbf {e} _{2}$ ett kodord. Därför, om vi tar emot $\mathbf {e} _{1},$ kan vi avkoda det antingen till $\mathbf {0}$ eller $\mathbf {c}$ . Däremot, om alla skurfel $\mathbf {e} _{1}$ och $\mathbf {e} _{2}$ inte ligger i samma coset, då är varje skurfel bestäms av dess syndrom. Felet kan sedan korrigeras genom dess syndrom. Således är en linjär kod $C$ en $\ell$ -burst-felkorrigerande kod om och endast om alla skurfel av längd $\leqslant \ell$ ligger i distinkta cosets av $C$ .

Teorem (kodordsklassificering av skurfel) — Låt $C$ vara en linjär $\ell$ -burst-felkorrigerande kod. Då kan ingen burst av längden $\leqslant 2\ell$ vara ett kodord.

Bevis

Låt $c$ vara ett kodord med en skur av längden $\leqslant 2\ell$ . Den har alltså mönstret $(0,1,u,v,1,0)$ , där $u$ och $v$ är ord av längd $\leqslant \ell -1.$ Därför är orden $w=(0,1,u,0,0,0 )$ och $cw=(0,0,0,v,1,0)$ är två skurar med längd $\leqslant \ell$ . För binära linjära koder tillhör de samma coset. Detta motsäger Distinct Cosets Theorem, därför kan ingen burst av längd $\leqslant 2\ell$ vara ett kodord.

Gränser för korrigering av skurfel

Övre gränser för detektering och korrigering av skurfel

Med övre gräns menar vi en gräns för vår feldetekteringsförmåga som vi aldrig kan gå längre än. Antag att vi vill designa en ${\displaystyle (n,k)}-$ kod som kan detektera alla skurfel med längden $\leqslant \ell .$ En naturlig fråga att ställa är: givet $n$ och $k$ , vad är det maximala $\ell$ som vi aldrig kan uppnå utöver? Med andra ord, vad är den övre gränsen för längden $\ell$ av skurar som vi kan detektera med vilken som helst ${\displaystyle (n,k)}-$ kod? Följande teorem ger ett svar på denna fråga.

Teorem (förmåga att upptäcka skurfel) — Förmågan att detektera skurfel för vilken som helst ${\displaystyle (n,k)}-$ kod är $\ell \leqslant nk.$

Bevis

Först observerar vi att en kod kan detektera alla skurar av längd $\leqslant \ell$ om och endast om inga två kodord skiljer sig åt med en skur av längd $\leqslant \ell$ . Antag att vi har två kodord $\mathbf {c} _{1}$ och $\mathbf {c} _{2}$ som skiljer sig åt med en burst $\mathbf { b}$ av längd $\leqslant \ell$ . När vi tar emot $\mathbf {c} _{1}$ kan vi inte avgöra om det överförda ordet verkligen är $\mathbf {c} _{1}$ utan överföringsfel, eller om det är $\mathbf {c} _{2}$ med ett skurfel $\mathbf {b}$ som inträffade under sändningen. Antag nu att vartannat kodord skiljer sig med mer än en skur av längd $\ell .$ Även om det överförda kodordet $\mathbf {c} _{1}$ träffas av en skur $\mathbf {b}$ med längd $\ell$ , kommer det inte att ändras till ett annat giltigt kodord. När vi tar emot det kan vi säga att detta är $\mathbf {c} _{1}$ med en burst $\mathbf {b} .$ Genom ovanstående observation vet vi att inga två kodord kan dela de första $n-\ell$ symbolerna. Anledningen är att även om de skiljer sig åt i alla andra $\ell$ -symboler, kommer de fortfarande att skilja sig åt med en längd ${\displaystyle \ell .} Därför$ uppfyller antalet kodord $q^{k}$${\displaystyle q^{k}\leqslant q^{n-\ell }.} Genom$ att applicera $\log _{q}$ på båda sidor och omarrangera, kan vi se att ${\ displaystyle \ell \leqslant nk}$ .

Nu upprepar vi samma fråga men för felkorrigering: givet $n$ och $k$ , vad är den övre gränsen för längden $\ell$ av skurar som vi kan korrigera med hjälp av någon $(n,k)$ kod? Följande teorem ger ett preliminärt svar på denna fråga:

Teorem (Förmåga att korrigera skurfel) — Förmågan att korrigera skurfel för vilken som helst ${\displaystyle (n,k)}-$ kod uppfyller $\ell \leqslant nk-\log _{q}(n-\ell )+2$

Bevis

Först observerar vi att en kod kan korrigera alla skurar av längd $\leqslant \ell$ om och bara om inga två kodord skiljer sig åt med summan av två skurar av längd $\leqslant \ell .$ Antag att två kodord $\mathbf {c} _{1}$ och $\mathbf {c} _{2}$ skiljer sig åt med skurar ${ \displaystyle \mathbf {b} _{1}}$ och $\mathbf {b} _{2}$ av längden $\leqslant \ell$ vardera. När vi fick $\mathbf {c} _{1}$ träffad av en burst $\mathbf {b} _{1}$ , kunde vi tolka det som om det var $\mathbf {c} _{2}$ träffad av en skur $-\mathbf {b} _{2}$ . Vi kan inte avgöra om det överförda ordet är $\mathbf {c} _{1}$ eller $\mathbf {c} _{2}$ . Anta nu att vartannat kodord skiljer sig med mer än två skurar av längd $\ell$ . Även om det överförda kodordet $\mathbf {c} _{1}$ träffas av en skur med längd $\ell$ , kommer det inte att se ut som ett annat kodord som har träffats av ett annat brista. För varje kodord $\mathbf {c} ,$ låt $B(\mathbf {c} )$ beteckna mängden av alla ord som skiljer sig från $\mathbf {c}$ med en skur av längd $\leqslant \ell .$ Lägg märke till att $B(\mathbf {c} )$ inkluderar själva ${\displaystyle \mathbf {c} } .$ Genom ovanstående observation vet vi att för två olika kodord $\mathbf {c} _{i}$ och $\mathbf {c} _{j},B (\mathbf {c} _{i})$ och $B(\mathbf {c} _{j})$ är disjunkta. Vi har $q^{k}$ kodord. Därför kan vi säga att $q^{k}|B(\mathbf {c} )|\leqslant q^{n}$ . Dessutom har vi $(n-\ell )q^{\ell -2}\leqslant |B(\mathbf {c} )|$ . Genom att plugga in den senare olikheten i den förra, sedan ta basen $q$ -logaritmen och omordna, får vi ovanstående sats.

Ett starkare resultat ges av Rieger bound:

Sats (Rieger bunden) — Om $\ell$ är felkorrigeringsförmågan för en $(n,k)$ linjär blockkod, då $2\ell \leqslant nk$ .

Bevis

Vilken linjär kod som helst som kan korrigera alla skurmönster av längd $\leqslant \ell$ kan inte ha en skur med längden $\leqslant 2\ell$ som kodord. Om den hade en skur med längden $\leqslant 2\ell$ som ett kodord, så skulle en skur med längden $\ell$ kunna ändra kodordet till ett skurmönster med längden $\ ell$ , som också kan erhållas genom att göra ett skurfel med längden $\displaystyle \ell }$ i alla nollkodord. Om vektorer inte är noll i de första $2\ell$ symbolerna, bör vektorerna vara från olika delmängder av en array så att deras skillnad inte är ett kodord av skurar med längden $2\ell$ . För att säkerställa detta villkor är antalet sådana delmängder åtminstone lika med antalet vektorer. Således skulle antalet delmängder vara minst $q^{2\ell }$ . Därför har vi minst $2\ell$ distinkta symboler, annars skulle skillnaden mellan två sådana polynom vara ett kodord som är summan av två skurar med längden $\leqslant \ell .$ Detta bevisar alltså Rieger Bound.

Definition. En linjär skurfelskorrigerande kod som uppnår ovanstående Rieger-gräns kallas en optimal skurfelskorrigerande kod.

Ytterligare gränser för korrigering av skurfel

Det finns mer än en övre gräns för den uppnåbara kodhastigheten för linjära blockkoder för multiple phased-burst correction (MPBC). En sådan gräns är begränsad till en maximal korrigerbar cyklisk skurlängd inom varje delblock, eller ekvivalent en begränsning på den minsta felfria längden eller gapet inom varje fasad skur. Denna gräns, när den reduceras till det speciella fallet av en gräns för enkelskurkorrigering, är Abramson-gränsen (en följd av Hamming-gränsen för skurfelskorrigering) när den cykliska skurlängden är mindre än halva blocklängden.

Sats (antal skurar) — För $1\leqslant \ell \leqslant {\tfrac {1}{2}}(n+1),$ över en binär alfabetet, det finns $n2^{\ell -1}+1$ vektorer med längden $n$ som är skurar med längden $\leqslant \ell$ .

Bevis

Eftersom skurlängden är $\leqslant {\tfrac {1}{2}}(n+1),$ finns det en unik skurbeskrivning associerad med skuren. Burst kan börja vid vilken som helst av de $n$ -positionerna i mönstret. Varje mönster börjar med $1$ och innehåller en längd på $\ell$ . Vi kan tänka oss det som mängden av alla strängar som börjar med $1$ och har längden $\ell$ . Det finns alltså totalt $2^{\ell -1}$ möjliga sådana mönster, och totalt $n2^{\ell -1}$ skurar av längd $\leqslant \ell .$ Om vi ​​inkluderar skuren helt noll, har vi $n2^{\ell -1}+1$ vektorer som representerar skurar med längden $\leqslant \ell .$

Sats (bunden till antalet kodord) — Om $1\leqslant \ell \leqslant {\tfrac {1}{2}}(n+1),$ en binär $\ell$ -burst felkorrigerande kod har som mest $2^{n}/(n2^{\ell -1}+1)$ kodord.

Bevis

Eftersom $\ell \leqslant {\tfrac {1}{2}}(n+1)$ vet vi att det finns $n2 ^{\ell -1}+1$ skurar av längd $\leqslant \ell$ . Säg att koden har $M$ kodord, då finns det $Mn2^{\ell -1}$ kodord som skiljer sig från ett kodord med en skur av längd $\ leqslant \ell$ . Vart och ett av $M$ -orden måste vara distinkta, annars skulle koden ha avstånd $<1$ . Därför innebär $M\leqslant 2^{n}/(n2^{\ell -1}+1).$$\displaystyle M(2^{\ell -1}+1)\leqslant 2^{n}}$ ⩽

Sats (Abramsons gränser) — Om $1\leqslant \ell \leqslant {\tfrac {1}{2}}(n+1)$ är en binär linjär $(n,k),\ell$ -burst felkorrigerande kod, dess blocklängd måste uppfylla:

$$n\leqslant 2^{nk-\ell +1}-1.$$

Bevis

För en linjär ${\displaystyle (n,k)}-$ kod finns det $2^{k}$ kodord. Genom vårt tidigare resultat vet vi det

$$2^{k}\leqslant {\frac {2^{n}}{n2^{\ell -1}+1}}.$$

Om vi ​​isolerar $n$ får vi $n\leqslant 2^{nk-\ell +1}-2^{-\ell + 1}$ . Eftersom $\ell \geqslant 1$ och $n$ måste vara ett heltal, har vi $n\leqslant 2^{nk- \ell +1}-1$ .

Anmärkning. $r=nk$ kallas redundansen för koden och i en alternativ formulering för Abramsons gränser är $r \geqslant \lceil \log _{2}(n+1)\rceil +\ell -1.$

Brandkoder

Medan cykliska koder i allmänhet är kraftfulla verktyg för att upptäcka skurfel, överväger vi nu en familj av binära cykliska koder som kallas brandkoder, som har goda möjligheter att korrigera fel i en skur. Med enkel skur, säg av längden $\ell$ , menar vi att alla fel som ett mottaget kodord har ligger inom ett fast intervall av $\ell$ siffror.

Låt $p(x)$ vara ett irreducerbart polynom med graden $m$ över $\mathbb {F} _{2}$ , och låt $p$ vara perioden av $p(x)$ . Perioden för ${\displaystyle p(x)} ,$ och faktiskt för vilket polynom som helst, definieras som det minsta positiva heltal $r$ så att $p(x)|x^{r}-1.$ Låt $\ell$ vara ett positivt heltal som uppfyller $\ell \leqslant m$ och $2\ell -1$ inte delbart med $p$ , där $p$ är perioden för $p(x)$ . Definiera brandkoden $G$ med följande generatorpolynom :

$$g(x)=\left(x^{2\ell -1}+1\right)p(x).$$

Vi kommer att visa att $G$ är en $\ell$ -burst-error correcting code.

Lemma 1 — $\gcd \left(p(x),x^{2\ell -1}+1\right)=1 .$

Bevis

Låt $d(x)$ vara den största gemensamma divisorn av de två polynomen. Eftersom $p(x)$ är irreducerbar, $\deg(d(x))=0$ eller ${\ displaystyle \deg(p(x))}$ . Antag $\deg(d(x))\neq 0,$ sedan $p(x)=cd(x)$ för någon konstant $c$ . Men $(1/c)p(x)$ är en divisor av $x^{2\ell -1}+1$ eftersom $d(x)$ är en divisor av $x^{2\ell -1}+1$ . Men detta motsäger vårt antagande att $p(x)$ inte delar $x^{2\ell -1}+1.$ Således $\deg(d(x))=0,$ som bevisar lemma.

Lemma 2 — Om $p(x)$ är ett polynom av period $p$ , då $p(x)|x^{k}-1$ om och endast om $p|k.$

Bevis

Om $p|k$ , sedan $x^{k}-1=( x^{p}-1)(1+x^{p}+x^{2p}+\dots +x^{k/p})$ . Således, $p(x)|x^{k}-1.$

Antag nu att $p(x)|x^{k}-1$ . Sedan, $k\geqslant p$ . Vi visar att $k$ är delbart med $p$ genom induktion på $k$ . Basfallet $k=p$ följer. Antag därför $k>p$ . Vi vet att $p(x)$ delar båda (eftersom den har period $p$ )

$$x^{p}-1=(x-1)\left(1+x+\dots +x^{p-1}\right)\quad {\text{and}}\quad x^{k }-1=(x-1)\left(1+x+\dots +x^{k-1}\höger).$$

Men $p(x)$ är irreducerbar, därför måste den dela båda $(1+x+\dots +x^{p-1} )$ och $(1+x+\dots +x^{k-1})$ ; sålunda delar den också skillnaden mellan de två sista polynomen, $x^{p}(1+x+\dots +x^{pk-1 })$ . Sedan följer att $p(x)$ delar $(1+x+\cdots +x^{pk-1})$ . Slutligen delar den också: $x^{kp}-1=(x-1)(1) +x+\dots +x^{pk-1})$ . Genom induktionshypotesen, $p|kp$ , sedan $p|k$ .

En följd av Lemma 2 är att eftersom $p(x)=x^{p}-1$ har period $p$ så har $p(x)$ delar $x^{k}-1$ om och endast om $p|k$ .

Teorem — Brandkoden är $\ell$ -burst felkorrigering

Om vi ​​kan visa att alla skurar av längd $\ell$ eller mindre förekommer i olika cosets kan vi använda dem som coset-ledare som bildar korrigerbara felmönster. Anledningen är enkel: vi vet att varje coset har en unik syndromavkodning associerad med sig, och om alla skurar av olika längd förekommer i olika cosets, har alla unika syndrom, vilket underlättar felkorrigering.

Bevis för teorem

Låt $x^{i}a(x)$ och $x^{j}b(x)$ vara polynom med grader ${\ displaystyle \ell _{1}-1}$ och $\ell _{2}-1$ , representerar skurar med längd $\ell _{1}$ och $\ell _{2}$ med $\ell _{1},\ell _{2}\leqslant \ell .$ Heltalen $i,j$ representerar startpositionerna för skurarna och är mindre än blocklängden för koden. För motsägelse skull, antag att $x^{i}a(x)$ och $x^{j}b(x)$ är i samma coset . Då $v(x)=x^{i}a(x)+x^{j}b(x)$ en giltigt kodord (eftersom båda termerna är i samma coset). Utan förlust av allmänhet, välj $i\leqslant j$ . Med divisionssatsen kan vi skriva: $ji=g(2\ell -1)+r,$ för heltal $g$ och $r,0\leqslant r<2\ell -1$ . Vi skriver om polynomet $v(x)$ enligt följande:

$$v(x)=x ^{i}a(x)+x^{i+g(2\ell -1)+r}=x^{i}a(x)+x^{i+g(2\ell -1)+ r}+2x^{i+r}b(x)=x^{i}\left(a(x)+x^{b}b(x)\höger)+x^{i+r}b( x)\left(x^{g(2\ell -1)}+1\höger)$$

Lägg märke till att vid den andra manipulationen introducerade vi termen $2x^{i+r}b(x)$ . Vi får göra det, eftersom brandkoder fungerar på $\mathbb {F} _{2}$ . Enligt vårt antagande $v(x)$ ett giltigt kodord och måste därför vara en multipel av $g(x)$ . Som nämnts tidigare, eftersom faktorerna för $g(x)$ är relativt primtal måste $v(x)$ vara delbara med ${\ displaystyle x^{2\ell -1}+1}$ . Om vi ​​tittar noga på det sista uttrycket som härleds för $v(x)$ lägger vi märke till att $x^{g(2\ell -1)}+1$ är delbart med $x^{2\ell -1}+1$ (av följden av Lemma 2). Därför $a(x)+x^{b}b(x)$ antingen delbart med $x^{2\ ell -1}+1$ eller är $0$ . Om vi ​​tillämpar divisionssatsen igen ser vi att det finns ett polynom $d(x)$ med graden $\delta$ så att:

$$a(x)+x^{b}b(x)=d(x)(x^ {2\ell -1}+1)$$

Då kan vi skriva:

$${\begin{aligned}\delta +2\ell -1&=\deg \left(d (x)\left(x^{2\ell -1}+1\höger)\höger)\\&=\deg \left(a(x)+x^{b}b(x)\höger)\ \&=\deg \left(x^{b}b(x)\right)&&\deg(a(x))=\ell _{1}-1<2\ell -1\\&=b+\ ell _{2}-1\end{aligned}}$$

Genom att likställa graden av båda sidorna får vi $b=2\ell -\ell _{2}+\delta .$ Eftersom $\ell _{1},\ell _{2}\leqslant \ell$ vi kan dra slutsatsen $b\geqslant \ell +\delta ,$ vilket innebär $b>\ell -1$ och $b>\delta$ . Lägg märke till att i expansionen:

$$a(x)+x^{b}b(x)=1+a_{1}x+a_{2}x^{2}+\dots +x^{\ell _{1}-1 }+x^{b}\left(1+b_{1}x+b_{2}x^{2}+\dots +x^{\ell _{2}-1}\höger).$$

Termen $x^{b}$ visas, men eftersom $\delta <b<2\ell -1$ , blir det resulterande uttrycket $d(x)(x^{2\ell -1}+1)$ innehåller inte $x^{b}$ , därför ${\ displaystyle d(x)=0}$ och därefter $a(x)+x^{b}b(x)=0.$ Detta kräver att $b=0$ och $a(x)=b(x)$ . Vi kan ytterligare revidera vår division av $ji$ med $g(2\ell -1)$ för att återspegla $b=0,$ dvs. $ji=g(2\ell -1)$ . Att ersätta tillbaka till $v(x)$ ger oss,

$$v(x)=x^{i}b(x)\left(x^{j-1}+1\höger).$$

Eftersom $\deg(b(x))=\ell _{2}-1<\ell$ , har $\deg(b(x))<\deg(p(x))=m$ . Men $p(x)$ är irreducerbar, därför måste $b(x)$ och $p(x)$ vara relativt primtal. Eftersom $v(x)$$) {\displaystyle p(x) )}$ ett kodord $x^{j-1}+1$ vara delbart med , eftersom det inte kan vara delbart med $x^{2\ell -1}+1$ . Därför $ji$ vara en multipel av $p$ . Men det måste också vara en multipel av $2\ell -1}$$n={\text{ lcm}}(2\ell -1,p)$ , vilket innebär att det måste vara en multipel av men det är precis kodens blocklängd. Därför $ji$ inte vara en multipel av $n$ eftersom de båda är mindre än $n$ . Således är vårt antagande om att $v(x)$ är ett kodord felaktigt, och därför är $x^{i}a(x)$ och $x^{j}b(x)$ finns i olika cosets, med unika syndrom, och därför korrigerbara.

Exempel: 5-skurfel vid korrigering av brandkod

Med teorin som presenteras i avsnittet ovan, överväg konstruktionen av en $5$ -burst felkorrigerande brandkod. Kom ihåg att för att konstruera en brandkod behöver vi ett irreducerbart polynom ${\displaystyle p(x)} ,$ ett heltal $\ell$ , som representerar skurfelskorrigeringsförmågan för vår kod, och vi måste tillfredsställ egenskapen att $2\ell -1$ inte är delbart med perioden för $p(x)$ . Med dessa krav i åtanke, överväg det irreducerbara polynomet $p(x)=1+x^{2}+x^{5}$ och låt $\ell =5$ . Eftersom $p(x)$ är ett primitivt polynom är dess period $2^{5}-1=31$ . Vi bekräftar att $2\ell -1=9$ inte är delbart med $31$ . Således,

$$g(x)=(x^{9 }+1)\left(1+x^{2}+x^{5}\right)=1+x^{2}+x^{5}+x^{9}+x^{11}+ x^{14}$$

är en brandkodsgenerator. Vi kan beräkna kodens blocklängd genom att utvärdera den minsta gemensamma multipeln av $p$ och $2\ell -1$ . Med andra ord, $n={\text{lcm}}(9,31)=279$ . Sålunda är brandkoden ovan en cyklisk kod som kan korrigera alla skurar med längden $5$ eller mindre.

Binära Reed-Solomon-koder

Vissa kodfamiljer, som Reed–Solomon , fungerar på alfabetstorlekar som är större än binära. Den här egenskapen ger sådana koder kraftfulla funktioner för korrigering av skurfel. Betrakta en kod som fungerar på $\mathbb {F} _{2^{m}}$ . Varje symbol i alfabetet kan representeras av $m$ bitar. Om $C$ är en $(n,k)$ Reed–Solomon-kod över $\mathbb {F} _{2^{m}}$ , vi kan tänka på $C$ som en $[mn,mk]_{2}$ kod över $\mathbb {F} _{2}$ .

Anledningen till att sådana koder är kraftfulla för skurfelskorrigering är att varje symbol representeras av $m$ -bitar, och i allmänhet är det irrelevant hur många av dessa $m$ -bitar som är felaktiga; oavsett om en enstaka bit, eller alla de $m$ -bitarna innehåller fel, är det ur ett avkodningsperspektiv fortfarande ett enda symbolfel. Med andra ord, eftersom skurfel tenderar att uppstå i kluster, finns det en stor möjlighet att flera binära fel bidrar till ett enda symbolfel.

Observera att en skur av ${\displaystyle (m+1)}-$ fel kan påverka högst $2$ -symboler, och en skur på $2m+1$ kan påverka vid de flesta $3$ symboler. Sedan kan en skur av $tm+1$ påverka högst $t+1$ symboler; detta innebär att en $t$ -symbols-error correcting code kan korrigera en skur av längd som mest $(t-1)m+1$ .

I allmänhet kan ett $t$ -fel som korrigerar Reed–Solomon-kod över $\mathbb {F} _{2^{m}}$ korrigera vilken kombination av

$${\frac {t}{1+\lgolv (l+m-2)/m\rgolv }}$$

eller färre skurar med längden $l$ , utöver att kunna korrigera $t$ -slumpmässiga värsta fel.

Ett exempel på en binär RS-kod

Låt $G$ vara en $[255,223,33]$ RS-kod över $\mathbb {F} _{2^{8}}$ . Denna kod användes av NASA i deras Cassini-Huygens rymdfarkost. Den kan korrigera $\lfloor 33/2\rfloor =16$ symbolfel. Vi konstruerar nu en binär RS-kod $G'$ från $G$ . Varje symbol kommer att skrivas med $\lceil \log _{2}(255)\rceil =8$ bitar. Därför kommer den binära RS-koden att ha $[2040,1784,33]_{2}$ som parametrar. Den kan korrigera vilken enskild skur med längden $l=121$ .

Interfolierade koder

Interleaving används för att konvertera faltningskoder från slumpmässiga felkorrigerare till burst-felkorrigerare. Grundtanken bakom användningen av interfolierade koder är att blanda ihop symboler vid sändaren. Detta leder till randomisering av skurar av mottagna fel som är nära placerade och vi kan sedan tillämpa analysen för slumpmässig kanal. Sålunda är huvudfunktionen som utförs av interfolieraren vid sändaren att ändra ingångssymbolsekvensen. Vid mottagaren kommer deinterleavern att ändra den mottagna sekvensen för att få tillbaka den ursprungliga oförändrade sekvensen vid sändaren.

Burst felkorrigerande kapacitet för interleaver

Illustration av rad- och kolumnstor ordning

Teorem — Om skurfelskorrigeringsförmågan hos någon kod är $\ell ,$ så är skurfelskorrigeringsförmågan hos dess $\lambda$ -vägsinterfoliering $\lambda \ell .$

Bevis

Antag att vi har en ${\displaystyle (n,k)}-$ kod som kan korrigera alla skurar med längden $\leqslant \ell .$ Interleaving kan ge oss en ${\displaystyle (\lambda n,\lambda k)}-$ kod som kan korrigera alla skurar av längd $\leqslant \lambda \ell ,$ för en given $\lambda$ . Om vi ​​vill koda ett meddelande med en godtycklig längd med interfoliering, delar vi först upp det i block med längden $\lambda k$ . Vi skriver $\lambda k$ -posterna för varje block i en $\lambda \times k$ -matris med rad-major-ordning. Sedan kodar vi varje rad med koden ${\displaystyle (n,k)} .$ Det vi får är en $\lambda \times n$ matris. Nu läses denna matris upp och sänds i kolumn-stor ordning. Tricket är att om det uppstår en skur med längden $h$ i det överförda ordet, så kommer varje rad att innehålla ungefär ${\tfrac {h}{\lambda }}$ på varandra följande fel (mer specifikt , kommer varje rad att innehålla en skur med längden minst $\lfloor {\tfrac {h}{\lambda }}\rfloor$ och högst $\lceil {\tfrac { h}{\lambda }}\rceil$ ). Om $h\leqslant \lambda \ell ,$ så ${\tfrac {h}{\lambda }}\leqslant \ell$ och ${ \displaystyle (n,k)}$ kod kan korrigera varje rad. Därför kan den interfolierade ${\displaystyle (\lambda n,\lambda k)}-$ koden korrigera skuren med längden $h$ . Omvänt, om $h>\lambda \ell ,$ så kommer minst en rad att innehålla fler än ${\tfrac {h}{\lambda }}$ på varandra följande fel, och ${\displaystyle (n,k)}-$ koden kanske misslyckas med att korrigera dem. Därför är felkorrigeringsförmågan hos den interfolierade ${\displaystyle (\lambda n,\lambda k)}-$ koden exakt $\lambda \ell .$ BEC-effektiviteten för den interfolierade koden förblir densamma som den ursprungliga ${\displaystyle (n,k)}-$ koden. Detta är sant eftersom:

$${\frac {2\lambda \ell }{\lambda n-\lambda k}}={\frac {2\ell }{nk}}$$

Blockera interleaver

Bilden nedan visar en 4 x 3 interleaver.

Ett exempel på en blockinterleaver

Ovanstående interfolierare kallas en blockinterleaver . Här skrivs ingångssymbolerna sekventiellt i raderna och utgångssymbolerna erhålls genom att läsa kolumnerna sekventiellt. Detta är alltså i form av $M\times N$ array. I allmänhet $N$ längden på kodordet.

Blockinterfolierarens kapacitet : För en $M\times N$ blockinterleaver och burst av längd $\ell ,$ är den övre gränsen för antalet fel ${\tfrac {\ell }{M}}.$ Detta är uppenbart från det faktum att vi läser utdatakolumnen och antalet rader är $M$ . Enligt satsen ovan för felkorrigeringskapacitet upp till $t,$ är den maximala tillåtna skurlängden $Mt.$ För skurlängd på $Mt+1$ kan avkodaren misslyckas.

Effektiviteten hos blockinterfolierare ( $\gamma$ ): Den hittas genom att ta förhållandet mellan skurlängden där avkodaren kan misslyckas med interfolierarens minne. Således kan vi formulera $\gamma$ som

$$\gamma ={\frac {Mt+1}{MN}}\approx {\frac {t}{N}}.$$

Nackdelar med blockinterleaver: Som det framgår av figuren läses kolumnerna sekventiellt, mottagaren kan tolka en rad endast efter att den tagit emot ett fullständigt meddelande och inte före det. Dessutom kräver mottagaren en avsevärd mängd minne för att lagra de mottagna symbolerna och måste lagra hela meddelandet. Dessa faktorer ger alltså upphov till två nackdelar, den ena är latensen och den andra är lagringen (ganska stor mängd minne). Dessa nackdelar kan undvikas genom att använda den faltningsinterfolierare som beskrivs nedan.

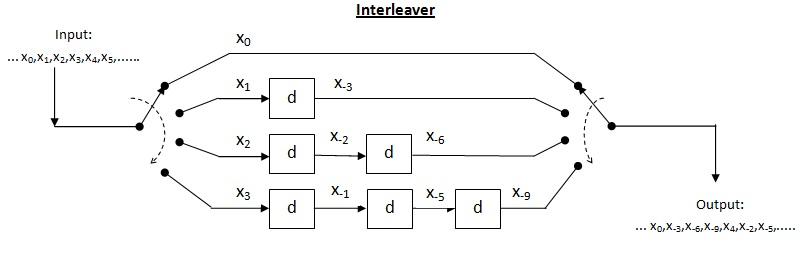
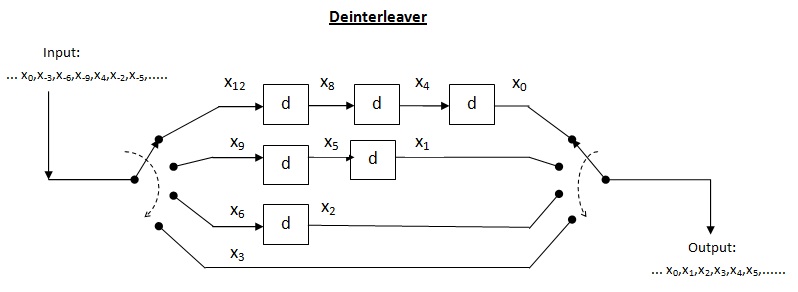
Konvolutionell interfolierare

Cross interleaver är ett slags multiplexer-demultiplexersystem. I detta system används fördröjningslinjer för att gradvis öka längden. Fördröjningslinje är i grunden en elektronisk krets som används för att fördröja signalen med en viss tidslängd. Låt $n$ vara antalet fördröjningslinjer och $d$ vara antalet symboler som introduceras av varje fördröjningsrad. Således är separationen mellan konsekutiva ingångar = $nd$ symboler. Låt längden på kodordet $\leqslant n.$ Således kommer varje symbol i inmatningskodordet att vara på en distinkt fördröjningslinje. Låt ett skurfel med längden $\ell$ inträffa. Eftersom separationen mellan på varandra följande symboler är $nd,$ antalet fel som den deinterfolierade utdatan kan innehålla ${\tfrac {\ell }{nd+1}}.$ Enligt satsen ovan, för felkorrigeringskapacitet upp till $t$ , är den maximala tillåtna skurlängden $(nd+1)(t-1).$ För skurlängd på $(nd+1)(t-1)+1,$ avkodaren kan misslyckas.

Ett exempel på en faltningsinterfolierare

Ett exempel på en deinterleaver

Effektiviteten för korsinterfolierare ( $\gamma$ ): Den hittas genom att ta förhållandet mellan skurlängden där avkodaren kan misslyckas med interfolierarens minne. I det här fallet kan interfolierarens minne beräknas som

$$(0+1+2+3+\cdots +(n-1))d={\frac {n(n-1)}{2}}d.$$

Således kan vi formulera $\gamma$ enligt följande:

$$\gamma ={\frac {(nd+1)(t-1)+1}{{\frac {n(n-1)}{2}}d}}.$$

Prestanda för korsinterfolierare: Såsom visas i ovanstående interfolierarfigur, är utmatningen ingenting annat än de diagonala symbolerna som genereras i slutet av varje fördröjningslinje. I det här fallet, när ingångsmultiplexomkopplaren slutför omkring halva omkopplingen, kan vi läsa första raden vid mottagaren. Således måste vi lagra maximalt cirka halva meddelandet vid mottagaren för att kunna läsa första raden. Detta minskar lagringsbehovet drastiskt med hälften. Eftersom bara ett halvt meddelande nu krävs för att läsa första raden, reduceras även latensen med hälften, vilket är en bra förbättring jämfört med blockinterfolieraren. Således delas det totala interfolierarminnet mellan sändare och mottagare.

Ansökningar

Kompakt disk

Utan felkorrigeringskoder skulle digitalt ljud inte vara tekniskt möjligt. Reed –Solomon-koderna kan korrigera en skadad symbol med ett enda bitfel lika enkelt som det kan korrigera en symbol med alla bitar fel. Detta gör RS-koderna särskilt lämpade för att korrigera skurfel. Den överlägset vanligaste tillämpningen av RS-koder är i cd-skivor. Förutom grundläggande felkorrigering som tillhandahålls av RS-koder, tillhandahålls skydd mot burst-fel på grund av repor på skivan av en korsinterleaver.

Det nuvarande digitala ljudsystemet för cd-skivor utvecklades av NV Philips i Nederländerna och Sony Corporation i Japan (avtal undertecknat 1979).

En kompaktskiva består av en 120 mm aluminiserad skiva belagd med en klar plastbeläggning, med spiralspår, cirka 5 km lång, som avsöks optiskt av en laser med våglängd ~0,8 μm, med en konstant hastighet av ~1,25 m/s. För att uppnå denna konstanta hastighet, varieras skivans rotation från ~8 varv/s under avsökning vid den inre delen av spåret till ~3,5 varv/s vid den yttre delen. Gropar och landområden är fördjupningarna (0,12 μm djupa) och platta segment som utgör binära data längs spåret (0,6 μm bredd).

CD-processen kan abstraheras som en sekvens av följande underprocesser:

• Kanalkodning av signalkällan
• Mekaniska delprocesser för att förbereda en masterskiva, producera användarskivor och känna av signalerna inbäddade på användarskivor under uppspelning – kanalen
• Avkodning av signalerna som avkänns från användarskivor

Processen är föremål för både burst-fel och slumpmässiga fel. Burst-fel inkluderar de som beror på skivmaterial (defekter i aluminiumreflekterande film, dåligt reflektionsindex för transparent skivmaterial), skivproduktion (fel under skivformning och skivskärning etc.), skivhantering (repor - i allmänhet tunna, radiella och ortogonala till inspelningsriktning) och variationer i uppspelningsmekanismen. Slumpmässiga fel inkluderar de som beror på jitter av rekonstruerad signalvåg och interferens i signal. CIRC ( Cross-Interleaved Reed–Solomon code ) är grunden för feldetektering och korrigering i CD-processen. Den korrigerar felskurar upp till 3 500 bitar i sekvens (2,4 mm långa som ses på CD-ytan) och kompenserar för felskurar upp till 12 000 bitar (8,5 mm) som kan orsakas av mindre repor.

Kodning: Ljudvågor samplas och omvandlas till digital form av en A/D-omvandlare. Ljudvågen samplas för amplitud (vid 44,1 kHz eller 44 100 par, ett vardera för vänster och höger kanal i stereoljudet). Amplituden vid en instans tilldelas en binär sträng med längden 16. Således producerar varje sampel två binära vektorer från $\mathbb {F} _{2}^{16}$ eller 4 ${\ displaystyle \mathbb {F} _{2}^{8}}$ byte data. Varje sekund av ljud som spelas in resulterar i 44 100 × 32 = 1 411 200 bitar (176 400 byte) data. Den samplade dataströmmen på 1,41 Mbit/s passerar genom felkorrigeringssystemet och omvandlas så småningom till en ström på 1,88 Mbit/s.

Ingången för kodaren består av ingångsramar var och en med 24 8-bitars symboler (12 16-bitars sampel från A/D-omvandlaren, 6 vardera från vänster och höger data (ljud) källor). En ram kan representeras av $L_{1}R_{1}L_{2}R_{2}\ldots L_{6}R_{6}$ där $L_{i}$ och $R_{i}$ är bytes från vänster och höger kanal från det ${\displaystyle i^{th}}-$ exemplet av ramen.

Inledningsvis permuteras byten för att bilda nya ramar representerade av $L_{1}L_{3}L_{5 }R_{1}R_{3}R_{5}L_{2}L_{4}L_{6}R_{2}R_{4}R_{6}$ där $L_{i },R_{i}$ representerar $i$ -th vänster och höger sampel från ramen efter 2 mellanliggande ramar.

Därefter kodas dessa 24 meddelandesymboler med C2 (28,24,5) Reed–Solomon-kod som är en förkortad RS-kod över $\mathbb {F} _{256}$ . Detta är tvåfelskorrigerande och har minsta avstånd 5. Detta lägger till 4 byte redundans, $P_{1}P_{2}$ bildar en ny ram: $L_{1}L_{3}L_{5}R_{1}R_{3}R_{5}P_{1 }P_{2}L_{2}L_{4}L_{6}R_{2}R_{4}R_{6}$ . Det resulterande kodordet med 28 symboler skickas genom en (28.4) korsinterfolierare som leder till 28 interfolierade symboler. Dessa skickas sedan genom C1 (32,28,5) RS-kod, vilket resulterar i kodord med 32 kodade utsignaler. Ytterligare omgruppering av udda numrerade symboler i ett kodord med jämna numrerade symboler för nästa kodord görs för att bryta upp eventuella korta skurar som fortfarande kan finnas efter ovanstående 4-ramsfördröjningsinterfoliering. För varje 24 ingångssymbol kommer det alltså att finnas 32 utgående symboler som ger $R=24/32$ . Slutligen läggs en byte av kontroll- och displayinformation till. Var och en av de 33 byten konverteras sedan till 17 bitar genom EFM (åtta till fjorton modulering) och tillägg av 3 sammanslagna bitar. Därför resulterar ramen med sex sampel i 33 byte × 17 bitar (561 bitar) till vilka adderas 24 synkroniseringsbitar och 3 sammanslagna bitar, vilket ger totalt 588 bitar.

Avkodning: CD-spelaren (CIRC-avkodare) tar emot dataströmmen med 32 utdatasymboler. Denna ström passerar först genom avkodaren Dl. Det är upp till individuella designers av CD-system att besluta om avkodningsmetoder och optimera deras produktprestanda. Med minsta avstånd 5 D1, D2-avkodarna kan var och en korrigera en kombination av $e$ -fel och $f$ -raderingar så att $2e+f<5$ . I de flesta avkodningslösningar är D1 utformad för att korrigera ett enda fel. Och vid mer än 1 fel, matar denna avkodare ut 28 raderingar. Avinterfolieraren i det efterföljande skedet fördelar dessa raderingar över 28 D2-kodord. Återigen i de flesta lösningar är D2 inställd på att endast hantera raderingar (en enklare och billigare lösning). Om fler än 4 raderingar skulle påträffas, matas 24 raderingar ut av D2. Därefter försöker ett feldöljande system att interpolera (från angränsande symboler) i händelse av okorrigerbara symboler, om inte ljud som motsvarar sådana felaktiga symboler dämpas.

Prestanda för CIRC: CIRC döljer långa bystfel genom enkel linjär interpolation. 2,5 mm spårlängd (4000 bitar) är den maximala fullständigt korrigerbara skurlängden. 7,7 mm spårlängd (12 300 bitar) är den maximala skurlängden som kan interpoleras. Samplingsinterpolationshastigheten är en var tionde timme vid Bit Error Rate (BER) $=10^{-4}$ och 1000 sampel per minut vid BER = $10^{-3}$ Oupptäckbara felexempel (klick): mindre än ett var 750:e timme vid BER = $10^{-3}$ och försumbar vid BER = $10^{-4}$ .

Se även

• Felsökning och korrigering
• Felrättande koder med återkoppling
• Kodpris
• Reed–Solomon felkorrigering