Tillåten regel

Den här artikeln handlar om inferensregler i logiska system. För begreppet i beslutsteori , se tillåten beslutsregel .

I logik är en inferensregel tillåten i ett formellt system om systemets satser inte ändras när den regeln läggs till de befintliga reglerna i systemet . Med andra ord, varje formel som kan härledas med den regeln är redan härledbar utan den regeln, så på sätt och vis är den överflödig. Begreppet en tillåten regel introducerades av Paul Lorenzen (1955).

Definitioner

Tillåtligheten har systematiskt studerats endast i fallet med strukturella (dvs substitutionsslutna ) regler i propositionella icke-klassiska logiker , som vi kommer att beskriva härnäst.

₀ Låt en uppsättning grundläggande propositionella kopplingar fixas (till exempel $\{\to ,\land ,\lor ,\bot \}$ i fallet med superintuitionistisk logik , eller $\{\to ,\bot ,\Box \}$ i fallet med monomodal logik ). Välformade formler byggs fritt med hjälp av dessa bindemedel från en räkningsbart oändlig uppsättning av propositionsvariabler p , p ₁ , .... En substitution σ är en funktion från formler till formler som pendlar med tillämpningar av konnektiven, dvs.

$\sigma f(A_{1},\dots ,A_{n})=f(\sigma A_ {1},\dots ,\sigma A_{n})$

för varje sammanbindande f , och formler A ₁ , ... , A _n . (Vi kan också tillämpa substitutioner på mängder Γ av formler, vilket gör att σ Γ = { σA : A ∈ Γ}. ) En konsekvensrelation i Tarski-stil är en relation $\vdash$ mellan uppsättningar av formler och formler, t.ex. den där

1. $A\vdash A,$
2. om $\Gamma \vdash A$ då $\Gamma ,\Delta \vdash A,$ ("försvagning")
3. om $\Gamma \vdash A$ och $\Delta ,A\vdash B$ då $\Gamma ,\Delta \vdash B,$ ("sammansättning")

för alla formler A , B och uppsättningar av formler Γ, Δ. En konsekvensrelation sådan att

4. om $\Gamma \vdash A$ så $\sigma \Gamma \vdash \sigma A$

för alla substitutioner kallas σ strukturell . (Observera att termen "strukturell" som den används här och nedan inte är relaterad till begreppet strukturella regler i efterföljande kalkyler .) En strukturell konsekvensrelation kallas en propositionell logik . En formel A är ett teorem för en logik $\vdash$ om $\varnothing \vdash A$ .

Till exempel identifierar vi en superintuitionistisk logik L med dess standardkonsekvensrelation $\vdash _{L}$ genererad av modus ponens och axiom, och vi identifierar en normal modal logik med dess globala konsekvensrelation $\vdash _{L}$ genererad av modus ponens, necessitation och (som axiom) logikens satser.

En strukturell slutledningsregel (eller bara regel för kort) ges av ett par (Γ, B ), vanligtvis skrivet som

${\frac {A_{1},\dots ,A_{n}}{B}}\qquad {\text{eller }}\qquad A_{1},\dots ,A_{n}/B,$

där Γ = { A ₁ , ... , _An } är en ändlig uppsättning formler och B är en formel. Ett exempel på regeln är

$\sigma A_{1},\dots ,\sigma A_{n}/\sigma B$

för en substitution σ . Regeln Γ/ B är deriverbar i $\vdash$ , om $\Gamma \vdash B$ . Det är tillåtet om σB för varje instans av regeln är ett sats när alla formler från σ Γ är satser. En regel är med andra ord tillåten om den, när den läggs till logiken, inte leder till nya satser. Vi skriver också $\Gamma \mathrel {|\!\!\!\sim } B$ om Γ/ B är tillåtet. (Observera att ${\phantom {.}}\!{|\!\!\!\sim }$ är en strukturell konsekvensrelation i sig.)

Varje härledbar regel är tillåten, men inte tvärtom i allmänhet. En logik är strukturellt komplett om varje tillåten regel är härledbar, dvs ${\vdash }={\,|\!\!\!\sim }$ .

I logiker med en väluppfostrad konjunktion (som superintuitionistisk eller modal logik) är en regel $A_{1},\dots ,A_{n}/B$ ekvivalent med $A_{1}\land \dots \land A_{n}/B$ med avseende på tillåtlighet och härledning. Det är därför vanligt att endast behandla unära regler A / B .

Exempel

• Klassisk propositionskalkyl ( CPC ) är strukturellt komplett. Antag faktiskt att A / B är en regel som inte kan härledas, och fixera en tilldelning v så att v ( A ) = 1 och v ( B ) = 0. Definiera en substitution σ så att för varje variabel p , σp = $\top$ om v ( p ) = 1, och σp = $\bot$ om v ( p ) = 0. Då är σA en sats, men σB är det inte (i själva verket är ¬ σB en sats). Regeln A / B är således inte heller tillåten. (Samma argument gäller för alla flervärdiga logiska L som är kompletta med avseende på en logisk matris vars alla element har ett namn på språket L .)
• Kreisel - Putnam -regeln (även känd som Harrops regel, eller independence of premiss rule )

$({\mathit {KPR}})\qquad {\frac {\neg p\to q\lor r}{(\neg p\to q)\lor (\neg p\to r)}}$

är tillåtet i den intuitionistiska propositionskalkylen ( IPC ). I själva verket är det tillåtet i varje superintuitionistisk logik. Å andra sidan, formeln

$(\neg p\to q\lor r)\to ((\ neg p\to q)\lor (\neg p\to r))$

är inte ett intuitionistiskt teorem; KPR är därför inte härledbar i IPC . I synnerhet IPC inte strukturellt komplett.

• Regeln

${\frac {\Box p}{p}}$

är tillåten i många modala logiker, såsom K , D , K 4, S 4, GL (se den här tabellen för namn på modala logiker ). Det är härledbart i S 4, men det går inte att härleda i K , D , K 4 eller GL .

• Regeln

${\frac {\Diamond p\land \Diamond \neg p}{\bot }}$

är tillåten i varje normal modal logik. Det är härledbart i GL och S 4.1, men det går inte att härleda i K , D , K 4, S 4 eller S 5.

• Löbs regel

$({\mathit {LR} })\qquad {\frac {\Box p\to p}{p}}$

är tillåtet (men inte härledbart) i den grundläggande modala logiken K , och det är härledbart i GL . LR är dock inte tillåten i K 4. Särskilt är det inte riktigt generellt att en regel som är tillåten i en logik L måste vara tillåten i sina förlängningar.

• Gödel –Dummett-logiken ( LC ), och den modala logiken Grz .3 är strukturellt kompletta. Produktens luddiga logik är också strukturellt komplett.

Beslutbarhet och reducerade regler

Den grundläggande frågan om tillåtna regler för en given logik är om uppsättningen av alla tillåtna regler är avgörbar . Observera att problemet är icke-trivialt även om logiken i sig (dvs. dess uppsättning satser) kan avgöras : definitionen av tillåtlighet av en regel A / B involverar en obegränsad universell kvantifierare över alla propositionella substitutioner. Därför a priori bara att tillåtligheten av regel i en avgörbar logik är $\Pi _{1}^{0}$ (dvs dess komplement är rekursivt uppräknad ). Till exempel är det känt att tillåtligheten i de bimodala logikerna K _u och K 4 _u (förlängningarna av K eller K 4 med den universella modaliteten) är obestämbar. Anmärkningsvärt är att beslutbarheten av tillåtlighet i den grundläggande modala logiken K är ett stort öppet problem.

₀ Ändå är det känt att reglernas tillåtlighet kan avgöras i många modala och superintuitionistiska logiker. De första beslutsförfarandena för tillåtna regler i grundläggande transitiva modala logiker konstruerades av Rybakov med hjälp av den reducerade formen av regler . En modal regel i variablerna p , ... , p _k kallas reducerad om den har formen

${\frac {\bigvee _{i=0}^{n} {\bigl (}\bigwedge _{j=0}^{k}\neg _{i,j}^{0}p_{j}\land \bigwedge _{j=0}^{k}\neg _ {i,j}^{1}\Box p_{j}{\bigr )}}{p_{0}}},$

där varje $\neg _{i,j}^{u}$ är antingen tomt eller negation $\neg$ . För varje regel r kan vi effektivt konstruera en reducerad regel s (kallad den reducerade formen av r ) så att vilken logik som helst medger (eller härleder) r om och endast om den tillåter (eller härleder) s , genom att införa extensionsvariabler för alla delformler i A och uttrycker resultatet i full disjunktiv normalform . Det räcker alltså att konstruera en beslutsalgoritm för tillåtlighet av reducerade regler.

Låt $\textstyle \bigvee _{i=0}^{n}\varphi _{i}/p_{0}$ vara en reducerad regel enligt ovan. Vi identifierar varje konjunktion $\varphi _{i}$ med mängden $\{\neg _{i ,j}^{0}p_{j},\neg _{i,j}^{1}\Box p_{j}\mid j\leq k\}$ av dess konjunkter. För varje delmängd W av mängden $\{\varphi _{i}\mid i\leq n\}$ av alla konjunktioner, låt oss definiera en Kripke-modell $M=\langle W,R,{\Vdash }\rangle$ av

$\varphi _{i}\Vdash p_{j}\iff p_{j}\in \varphi _{i},$

$\varphi _{i}\,R\,\varphi _{i'}\iff \forall j\leq k\,(\Box p_{j}\in \varphi _{i}\Högerpil \{ p_{j},\Box p_{j}\}\subseteq \varphi _{i'}).$

Sedan ger följande ett algoritmiskt kriterium för tillåtlighet i K 4:

Sats . Regeln ${\displaystyle \textstyle \bigvee _{i=0}^{n}\varphi _{i}/p_{0}} är inte$ tillåten i K 4 om och endast om det finns existerar en mängd $W\subseteq \{\varphi _{i}\mid i\leq n\}$ så att

1. $\varphi _{i}\nVdash p_{0}$ för vissa $i\leq n,$
2. $\varphi _{i}\Vdash \varphi _{i}$ för varje $i\leq n,$
3. för varje delmängd D av W finns det element $\alpha ,\beta \in W$ så att ekvivalenserna

$\alpha \Vdash \Box p_{j}$ om och endast om $\varphi \Vdash p_{j}\land \Box p_{j}$ för varje $\varphi \in D$

$\alpha \Vdash \Box p_{j}$ om och endast om $\alpha \Vdash p_ {j}$ och $\varphi \Vdash p_{j}\land \Box p_{j}$ för varje $\varphi \in D$

håller för alla j .

Liknande kriterier kan hittas för logikerna S4 , GL och Grz . Dessutom kan tillåtlighet i intuitionistisk logik reduceras till tillåtlighet i Grz med hjälp av Gödel–McKinsey–Tarski-översättningen :

$A\,|\!\!\!\sim _{IPC}B$ om och endast om $T(A)\,|\!\!\!\sim _{Grz}T(B).$

Rybakov (1997) utvecklade mycket mer sofistikerade tekniker för att visa att tillåtligheten kan avgöras, vilka gäller en robust (oändlig) klass av transitiva (dvs. utvidgning av K 4 eller IPC ) modala och superintuitionistiska logiker, inklusive t.ex. S 4.1, S 4.2, S 4.3 , KC , Tk (liksom de ovan nämnda logikerna IPC _, K4 , S4 , GL , Grz ) .

Trots att det kan avgöras har tillåtlighetsproblemet relativt hög beräkningskomplexitet , även i enkla logiker: tillåtligheten av regler i de grundläggande transitiva logikerna IPC , K 4, S 4, GL , Grz är coNEXP -komplett. Detta bör jämföras med härledningsproblemet (för regler eller formler) i dessa logiker, som är PSPACE -komplett.

Projektivitet och enande

Tillåtlighet i propositional logik är nära besläktad med förening i ekvationsteorin för modal eller Heyting algebras . Anslutningen utvecklades av Ghilardi (1999, 2000). I den logiska uppställningen är en förenare av en formel A på språket för en logisk L (en L -förenare för kort) en substitution σ så att σA är en sats av L . (Med detta begrepp kan vi omformulera tillåtligheten av en regel A / B i L som "varje L -förenare av A är en L -förenare av B ".) En L -förenare σ är mindre allmän än en L -förenare τ , skrivs som σ ≤ τ , om det finns en substitution υ sådan att

$\vdash _{L}\sigma p\leftrightarrow \upsilon \tau p$

för varje variabel p . En komplett uppsättning förenare av en formel A är en uppsättning S av L -förenare av A så att varje L -förenare av A är mindre generell än någon förenare från S. En mest allmän förenare (MGU) av A är en förenare σ så att { σ } är en komplett uppsättning av förenare av A . Det följer att om S är en komplett uppsättning av förenare av A , så är en regel A / B L - tillåten om och endast om varje σ i S är en L -förenare av B. Således kan vi karakterisera tillåtna regler om vi kan hitta väluppfostrade kompletta uppsättningar av förenare.

En viktig klass av formler som har ett mest allmänt förenande är de projektiva formlerna : dessa är formler A så att det finns en förenare σ av A så att

$A\vdash _{L}B\leftrightarrow \sigma B$

för varje formel B . Observera att σ är en MGU av A . I transitiva modala och superintuitionistiska logiker med den finita modellegenskapen kan man karakterisera projektiva formler semantiskt som de vars uppsättning finita L -modeller har förlängningsegenskapen : om M är en finit Kripke L -modell med en rot r vars kluster är en singelton . , och formeln A gäller vid alla punkter i M utom för r , då kan vi ändra värderingen av variabler i r för att göra A sann vid r också. Dessutom ger beviset en explicit konstruktion av en MGU för en given projektiv formel A .

I de grundläggande transitiva logikerna IPC , K 4, S 4, GL , Grz (och mer allmänt i vilken transitiv logik som helst med den finita modellegenskapen vars uppsättning av finita ramar uppfyller en annan typ av extensionsegenskap), kan vi effektivt konstruera för vilken formel A som helst . dess projektiva approximation Π( A ): en ändlig uppsättning projektiva formler så att

1. $P\vdash _{L}A$ för varje $P\in \Pi (A),$
2. varje förenare av A är en förenare av en formel från Π( A ).

Härav följer att uppsättningen av MGU:er av element i Π( A ) är en komplett uppsättning förenare av A . Dessutom, om P är en projektiv formel, då

$P\,|\!\!\!\sim _{L}B$ om och endast om $P\vdash _{L}B$

för vilken formel B som helst . Således får vi följande effektiva karaktärisering av tillåtna regler:

$A\,|\!\!\!\sim _{L}B$ om och endast om $\forall P\in \Pi (A)\,(P\vdash _{L}B).$

Grunder för tillåtna regler

Låt L vara en logik. En uppsättning R av L -tillåtliga regler kallas en grund för tillåtliga regler, om varje tillåten regel Γ/ B kan härledas från R och de härledbara reglerna för L , med hjälp av substitution, sammansättning och försvagning. Med andra ord R en grund om och endast om ${\displaystyle {\phantom {.}}\!{|\!\!\!\sim _{L}}} är den minsta strukturella$ konsekvensrelationen som inkluderar $\vdash _{L}$ och R. _

Lägg märke till att avgörbarheten av tillåtliga regler av en avgörbar logik är likvärdig med förekomsten av rekursiva (eller rekursivt uppräknbara ) baser: å ena sidan är uppsättningen av alla tillåtliga regler en rekursiv grund om tillåtligheten kan avgöras. Å andra sidan är uppsättningen av tillåtna regler alltid ko-rekursivt uppräknbar, och om vi vidare har en rekursivt uppräknbar grund, är uppsättningen av tillåtna regler också uppräknbar rekursivt; därför är det avgörbart. (Med andra ord, vi kan avgöra tillåtligheten av A / B genom följande algoritm : vi startar parallellt två uttömmande sökningar , en för en substitution σ som förenar A men inte B , och en för en härledning av A / B från R och $\vdash _{L}$ En av sökningarna måste så småningom ge ett svar.) Bortsett från beslutbarhet, är explicita grunder för tillåtna regler användbara för vissa tillämpningar, t.ex. i beviskomplexitet .

För en given logik kan vi fråga om den har en rekursiv eller finit grund av tillåtna regler, och att tillhandahålla en explicit grund. Om en logik inte har någon ändlig bas, kan den ändå ha en oberoende bas : en bas R så att ingen riktig delmängd av R är en bas.

I allmänhet kan mycket lite sägas om förekomsten av baser med önskvärda egenskaper. Till exempel, medan tabelllogiker i allmänhet är väluppfostrade och alltid ändligt axiomatiserbara, finns det tabellformade modala logiker utan en ändlig eller oberoende grund av regler. Finita baser är relativt sällsynta: även de grundläggande transitiva logikerna IPC , K 4, S 4, GL , Grz har inte en finit grund av tillåtna regler, även om de har oberoende baser.

Exempel på baser

• Den tomma uppsättningen är en grund för L -godkända regler om och endast om L är strukturellt komplett.
• Varje förlängning av den modala logiken S 4.3 (inklusive, i synnerhet, S 5) har en ändlig grund som består av den enda regeln

${\frac {\Diamond p\land \Diamond \neg p}{\bot }}.$

• Visser s regler

${\frac {\displaystyle {\Bigl (}\bigwedge _{i=1}^{n}(p_{i}\to q_{i})\to p_{n+1}\lor p_{n+2}{\Bigr )}\lor r }{\displaystyle \bigvee _{j=1}^{n+2}{\Bigl (}\bigwedge _{i=1}^{n}(p_{i}\to q_{i})\to p_ {j}{\Bigr )}\lor r}},\qquad n\geq 1$

är en grund för tillåtna regler i IPC eller KC .

• Reglerna

${\displaystyle {\frax {\Bigl (}\Box q\to \bigvee _{i=1}^{n}\Box p_{i}{\Bigr )}\lor \Box r}{\displaystyle \bigvee _{i=1} ^{n}\Box (q\land \Box q\to p_{i})\lor r}},\qquad n\geq 0} är en grund för tillåtna regler$

för GL . (Observera att den tomma disjunktionen definieras som $\bot$ )

${\frac {\displaystyle \Box {\Bigl (}\Box (q\to \Box q)\to \bigvee _{i=1}^{n} \Box p_{i}{\Bigr )}\lor \Box r}{\displaystyle \bigvee _{i=1}^{n}\Box (\Box q\to p_{i})\lor r}} ,\qquad n\geq 0$

är en grund för tillåtna regler för S 4 eller Grz .

• Reglerna

Semantik för tillåtna regler

En regel Γ/ B är giltig i en modal eller intuitionistisk Kripke-ram $F=\langle W,R\rangle$ , om följande är sant för varje värdering $\Vdash$ i F :

om för alla $A\in \Gamma$$\forall x\in W\,(x\Vdash A)$ , då $\forall x\in W\,(x\Vdash B)$ .

(Definitionen generaliserar lätt till allmänna ramar , om det behövs.)

Låt X vara en delmängd av W , och t en punkt i W . Vi säger att det är det

• en reflexmässig tight föregångare till X , om för varje y i W : t R y om och endast om t = y eller för några x i X : x = y eller x R y ,
• en irreflexiv tight föregångare till X , om för varje y i W : t R y om och endast om för några x i X : x = y eller x R y .

Vi säger att en ram F har reflexiva (irreflexiva) snäva föregångare, om det för varje finit delmängd X av W finns en reflexiv (irreflexiv) tight föregångare till X i W .

Vi har:

• en regel är tillåten i IPC om och endast om den är giltig i alla intuitionistiska ramar som har reflexmässiga tighta föregångare,
• en regel är tillåten i K 4 om och endast om den är giltig i alla transitiva ramar som har reflexiva och irreflexiva täta föregångare,
• en regel är tillåten i S 4 om och endast om den är giltig i alla transitiva reflexiva ramar som har reflexiva tighta föregångare,
• en regel är tillåten i GL om och endast om den är giltig i alla transitiva omvända välgrundade ramar som har irreflexiva tighta föregångare.

Observera att bortsett från några triviala fall måste ramar med snäva föregångare vara oändliga. Därför åtnjuter inte tillåtna regler i grundläggande transitiva logiker den finita modellegenskapen.

Strukturell fullständighet

Även om en allmän klassificering av strukturellt kompletta logiker inte är en lätt uppgift, har vi en god förståelse för vissa specialfall.

Intuitionistisk logik i sig är inte strukturellt komplett, men dess fragment kan bete sig annorlunda. Varje disjunktionsfri regel eller implikationsfri regel som är tillåtna i en superintuitionistisk logik är nämligen härledbar. Å andra sidan härskar myntverket

${\frac {(p\to q)\to p\lor r}{( (p\to q)\to p)\lor ((p\to q)\to r)}}$

är tillåtet i intuitionistisk logik men inte härledbart och innehåller endast implikationer och disjunktioner.

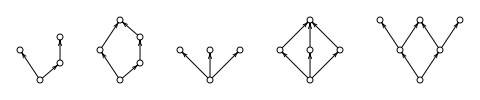
Vi känner till de maximala strukturellt ofullständiga transitiva logikerna. En logik kallas ärftligt strukturellt komplett , om någon förlängning är strukturellt komplett. Till exempel är klassisk logik, liksom logikerna LC och Grz .3 som nämnts ovan, ärftligt strukturellt kompletta. En fullständig beskrivning av ärftligt strukturellt kompletta superintuitionistiska och transitiva modala logiker gavs av Citkin respektive Rybakov. En superintuitionistisk logik är nämligen ärftligt strukturellt komplett om och bara om den inte är giltig i någon av de fem Kripke-ramarna

På liknande sätt är en förlängning av K 4 ärftligt strukturellt fullständig om och endast om den inte är giltig i någon av vissa tjugo Kripke-ramar (inklusive de fem intuitionistiska ramarna ovan).

Det finns strukturellt kompletta logiker som inte är ärftligt strukturellt kompletta: till exempel är Medvedevs logik strukturellt komplett, men den ingår i den strukturellt ofullständiga logiken KC .

Varianter

En regel med parametrar är en formregel

${A(p_{1} ,\dots ,p_{n},s_{1},\dots ,s_{k})}{B(p_{1},\dots,p_{n},s_{1},\dots ,s_{k })}},}$

vars variabler är uppdelade i de "vanliga" variablerna pi , _och parametrarna si _. Regeln är L -tillåten om varje L -förenare σ av A så att σs _i = s _i för varje i också är en förenare av B . De grundläggande beslutbarhetsresultaten för tillåtliga regler överensstämmer också med regler med parametrar.

En regel med flera slutsatser är ett par (Γ,Δ) av två ändliga uppsättningar formler, skrivna som

${\frac {A_{1},\dots ,A_{n}}{B_{1},\dots ,B_{m}}}\qquad {\text{eller}}\qquad A_{1} ,\dots ,A_{n}/B_{1},\dots ,B_{m}.$

En sådan regel är tillåten om varje förenare av Γ också är en förenare av någon formel från Δ. Till exempel är en logisk L konsekvent om den tillåter regeln

${\frac {\;\bot \;}{}},$

och en superintuitionistisk logik har disjunktionsegenskapen om den medger regeln

${\frac {p\lor q}{p,q}}.$

Återigen, grundläggande resultat om tillåtna regler generaliseras smidigt till regler med flera slutsatser. I logiker med en variant av disjunktionsegenskapen har multipla-slutslutningsreglerna samma uttryckskraft som enkelslutningsregler: till exempel i S 4 är regeln ovan ekvivalent med

${\frac {A_{1},\dots ,A_{n}}{\Box B_{1}\lor \dots \lor \Box B_{m}}}.$

Icke desto mindre kan regler med flera slutsatser ofta användas för att förenkla argument.

I bevisteorin betraktas tillåtlighet ofta i samband med sequent calculi , där de grundläggande objekten är sekvenser snarare än formler. Till exempel kan man omformulera cut-elimineringssatsen som att den cut-free sekvenskalkylen medger cut-regeln

${\frac {\Gamma \vdash A,\Delta \qquad \Pi ,A\vdash \Lambda }{\Gamma ,\Pi \vdash \Delta ,\Lambda }}.$

(Genom språkmissbruk sägs det också ibland att den (fullständiga) sekvenskalkylen medger skärning, vilket betyder att dess klippfria version gör det.) Tillåtligheten i sekventiella kalkyler är dock vanligtvis bara en notationsvariant för tillåtlighet i motsvarande logik: någon komplett kalkyl för (säg) intuitionistisk logik tillåter en sekventuell regel om och endast om IPC medger formelregeln som vi får genom att översätta varje sekvent $\Gamma \vdash \Delta$ till dess karakteristiska formel $\bigwedge \Gamma \to \bigvee \Delta$ .

Anteckningar

• W. Blok, D. Pigozzi, Algebraizable logics , Memoirs of the American Mathematical Society 77 (1989), nr. 396, 1989.
•   A. Chagrov och M. Zakharyaschev, Modal Logic , Oxford Logic Guides vol. 35, Oxford University Press, 1997. ISBN 0-19-853779-4
• P. Cintula och G. Metcalfe, Structural completeness in fuzzy logics , Notre Dame Journal of Formal Logic 50 (2009), nr. 2, s. 153–182. doi : 10.1215/00294527-2009-004
• AI Citkin, On structurally complete superintuitionistic logics , Soviet Mathematics - Doklady, vol. 19 (1978), sid. 816-819.
• S. Ghilardi, Unification in intuitionistic logic , Journal of Symbolic Logic 64 (1999), nr. 2, s. 859–880. Projekt Euclid JSTOR
• S. Ghilardi, Best solving modal equations , Annals of Pure and Applied Logic 102 (2000), nr. 3, s. 183–198. doi : 10.1016/S0168-0072(99)00032-9
• R. Iemhoff, On the admissible rules of intuitionistic propositional logic , Journal of Symbolic Logic 66 (2001), nr. 1, s. 281–294. Projekt Euclid JSTOR
• R. Iemhoff, Intermediate logics and Vissers rules , Notre Dame Journal of Formal Logic 46 (2005), nr. 1, s. 65–81. doi : 10.1305/ndjfl/1107220674
• R. Iemhoff, On the rules of intermediate logics , Archive for Mathematical Logic , 45 (2006), nr. 5, s. 581–599. doi : 10.1007/s00153-006-0320-8
• E. Jeřábek, Admissible rules of modal logics , Journal of Logic and Computation 15 (2005), nr. 4, s. 411–431. doi : 10.1093/logcom/exi029
• E. Jeřábek, Complexity of admissible rules , Archive for Mathematical Logic 46 (2007), nr. 2, s. 73–92. doi : 10.1007/s00153-006-0028-9
• E. Jeřábek, Oberoende grunder för tillåtna regler , Logic Journal of the IGPL 16 (2008), nr. 3, s. 249–267. doi : 10.1093/jigpal/jzn004
•   M. Kracht, Modal Consequence Relations , i: Handbook of Modal Logic (P. Blackburn, J. van Benthem och F. Wolter, red.), Studies of Logic and Practical Reasoning vol. 3, Elsevier, 2007, s. 492–545. ISBN 978-0-444-51690-9
• P. Lorenzen, Einführung in die operative Logik und Mathematik , Grundlehren der mathematischen Wissenschaften vol. 78, Springer–Verlag, 1955.
• G. Mints och A. Kojevnikov, Intuitionistiska Frege-system är polynomiellt ekvivalenta , Zapiski Nauchnyh Seminarov POMI 316 (2004), s. 129–146. gzippad PS
• T. Prucnal, Strukturell fullständighet av Medvedevs propositionskalkyl , Reports on Mathematical Logic 6 (1976), s. 103–105.
• T. Prucnal, On two problems of Harvey Friedman , Studia Logica 38 (1979), nr. 3, s. 247–262. doi : 10.1007/BF00405383
• P. Rozière, Règles admissibles en calcul propositionnel intuitionniste , Ph.D. avhandling, Université de Paris VII , 1992. PDF
•   VV Rybakov, Admissibility of Logical Inference Rules , Studies in Logic and the Foundations of Mathematics vol. 136, Elsevier, 1997. ISBN 0-444-89505-1
• F. Wolter, M. Zakharyaschev, Undecidability of the unification and admissibility problems for modal and description logics , ACM Transactions on Computational Logic 9 (2008), nr. 4, artikelnr. 25. doi : 10.1145/1380572.1380574 PDF