Termisk motstånd i gränssnittet

Termisk gränsresistans , även känd som termisk gränsresistans , eller Kapitza-resistans , är ett mått på motståndet mot termiskt flöde vid gränsytan mellan två material. Även om dessa termer kan användas omväxlande, hänvisar Kapitza-resistens tekniskt till ett atomiskt perfekt, platt gränssnitt medan termisk gränsresistans är en bredare term. Denna termiska resistans skiljer sig från kontaktresistans (inte att förväxla med elektrisk kontaktresistans ) eftersom den existerar även vid atomiskt perfekta gränssnitt. På grund av skillnader i elektroniska och vibrationsegenskaper hos olika material, när en energibärare (fonon eller elektron, beroende på material) försöker passera gränssnittet, kommer den att spridas vid gränssnittet. Sannolikheten för överföring efter spridning kommer att bero på de tillgängliga energitillstånden på sida 1 och sida 2 av gränssnittet.

Om man antar att ett konstant termiskt flöde appliceras över ett gränssnitt, kommer detta termiska gränsmotstånd att leda till en ändlig temperaturdiskontinuitet vid gränssnittet. Från en förlängning av Fouriers lag kan vi skriva

$Q={\frac {\Delta T}{R}}=G\Delta T$

där $Q$ är det applicerade flödet, $\Delta T$ är det observerade temperaturfallet, $R$ är det termiska gränsmotståndet och $G$ är dess invers, eller termisk gränskonduktans.

Att förstå den termiska resistansen vid gränssnittet mellan två material är av primär betydelse vid studiet av dess termiska egenskaper. Gränssnitt bidrar ofta väsentligt till materialens observerade egenskaper. Detta är ännu mer kritiskt för i nanoskala där gränssnitt avsevärt kan påverka egenskaperna i förhållande till bulkmaterial.

Lågt termiskt motstånd vid gränssnitt är tekniskt viktigt för applikationer där mycket hög värmeavledning är nödvändig. Detta är särskilt oroande för utvecklingen av mikroelektroniska halvledarenheter enligt definitionen av International Technology Roadmap for Semiconductors 2004, där en 8 nm enhetsstorlek förväntas generera upp till 100 000 W/cm 2 och skulle behöva effektiv värmeavledning av ^en förväntad munstycksnivåvärmeflöde på 1000 W/cm ² vilket är en storleksordning högre än nuvarande anordningar. Å andra sidan skulle applikationer som kräver god termisk isolering, såsom jetmotorturbiner, dra nytta av gränssnitt med högt termiskt motstånd. Detta skulle också kräva materialgränssnitt som är stabila vid mycket hög temperatur. Exempel är metall-keramiska kompositer som för närvarande används för dessa applikationer. Högt termiskt motstånd kan också uppnås med flerskiktssystem.

Som nämnts ovan beror termisk gränsresistans på bärarspridning vid ett gränssnitt. Vilken typ av bärare som sprids beror på materialen som styr gränssnitten. Till exempel, vid ett metall-metallgränssnitt kommer elektronspridningseffekter att dominera termisk gränsresistans, eftersom elektroner är de primära termiska energibärarna i metaller.

Två mycket använda prediktiva modeller är den akustiska missanpassningsmodellen (AMM) och den diffusa missanpassningsmodellen (DMM). AMM antar ett geometriskt perfekt gränssnitt och fonontransport över den är helt elastisk och behandlar fononer som vågor i ett kontinuum. Å andra sidan antar DMM:n att spridningen vid gränssnittet är diffusiv, vilket är korrekt för gränssnitt med karakteristisk grovhet vid förhöjda temperaturer.

Molecular dynamics (MD)-simuleringar är ett kraftfullt verktyg för att undersöka termisk resistans i gränsytan. Nyligen genomförda MD-studier har visat att den termiska motståndskraften mellan fast-vätskor och gränsytorna reduceras på nanostrukturerade fasta ytor genom att förbättra interaktionsenergin mellan fast och vätska per ytenhet och minska skillnaden i vibrationstäthet i tillstånd mellan fast och flytande.

Teoretiska modeller

Den primära modellen som historiskt har beskrivit Kapitza-resistens är fonongasmodellen. Inom denna modell finns modellerna för akustisk missanpassning och diffus missanpassning (AMM respektive DMM). För båda modellerna antas gränssnittet bete sig exakt som bulken på vardera sidan av gränssnittet (t.ex. bulk-fonondispersioner, hastigheter, etc.), med hybridvibrationslägen och fononerna som upptar dem är helt försummade. Dessutom är AMM- och DMM-modellerna endast baserade på elastisk fonontransport, vanligtvis bortser man från elektriska bidrag, även om det är möjligt att ta hänsyn till elektronbidrag inom fonongasmodellen. AMM- och DMM-modellerna bör gälla för gränssnitt där minst ett av materialen är elektriskt isolerande. Det termiska motståndet resulterar sedan från överföringen av fononer över gränssnittet. Energi överförs när högre energifononer som finns i högre densitet i det varmare materialet fortplantar sig till det kallare materialet, vilket i sin tur överför lägre energifononer, vilket skapar ett nettoenergiflöde .

Enligt AMM- och DMM-modellerna är en avgörande faktor för att bestämma den termiska resistansen vid ett gränssnitt överlappningen av fonontillstånd . Specifikt bortser modellerna helt från effekterna av oelastisk spridning och multipla fononinteraktioner. Till exempel tillåter modellerna endast att en fonon som upptar en viss modfrekvens interagerar med en annan fonon som upptar ett mod med exakt samma frekvens. I verkligheten är detta dock inte fallet och interaktionssannolikheten för två fononer kan beräknas med hjälp av störningsteori (kvantmekanik) . Som ett exempel inom AMM- och DMM-modellerna, givet två material A och B, om material A har en låg population (eller ingen population) av fononer med ett visst k-värde, kommer det att finnas mycket få fononer av den vågvektorn (eller motsvarande frekvens ) . ) för att fortplanta sig från A till B. På samma sätt, på grund av principen om detaljerad balans , förutspår AMM och DMM att mycket få fononer av den vågvektorn kommer att fortplanta sig i motsatt riktning, från B till A, även om material B har en stor population av fononer med den vågvektorn. Eftersom överlappningen mellan fonondispersioner är liten, finns det färre lägen för att tillåta värmeöverföring i materialet, vilket ger ett högt termiskt gränsytemotstånd i förhållande till material med en hög grad av överlappning. Ingen av modellerna är särskilt effektiva för att förutsäga den termiska gränssnittsresistansen (med undantag för mycket låg temperatur), utan snarare för de flesta material fungerar de som övre och nedre gränser för verkligt beteende.

AMM och DMM skiljer sig åt i de förhållanden de kräver för spridning över gränssnittet, eftersom modellerna skiljer sig mycket åt i deras behandling av spridning vid gränssnittet. I AMM antas gränssnittet vara perfekt, vilket resulterar i ingen spridning, sålunda sprider sig fononer elastiskt över gränssnittet. Vågvektorerna som utbreder sig över gränssnittet bestäms av bevarande av momentum. I DMM antas den motsatta ytterligheten, ett perfekt spridande gränssnitt. I detta fall är vågvektorerna som utbreder sig över gränssnittet slumpmässiga och oberoende av infallande fononer på gränssnittet. För båda modellerna måste den detaljerade balansen fortfarande följas.

För båda modellerna gäller de grundläggande ekvationerna för fonongasmodellen. Energiflödet från ett material till det andra i en dimension är bara:

$Q_{1,2}=\summa _{k}n\left(k,T_{ 1}\right)E\nu \alpha \left(k,T_{1},T_{2}\right)$

där $\nu$ är grupphastigheten som uppskattas vara ljudhastigheten i materialet för AMM- och DMM-modellerna, $n\left(k,T_{1 }\right)$ är antalet fononer vid en given vågvektor, E är energin och α är sannolikheten för överföring över gränssnittet. Nettoflödet är alltså skillnaden mellan energiflödena:

$Q_{net}\ =\ Q_{1,2}\ -\ Q_{2,1}$

Eftersom båda flödena är beroende av T ₁ och T ₂ , kan förhållandet mellan flödet och temperaturskillnaden användas för att bestämma den termiska gränssnittsresistansen baserat på:

$R_{th}\ =\ {\frac {\Delta T}{Q/A}}$

där A är gränssnittets area. Dessa grundläggande ekvationer ligger till grund för båda modellerna. n bestäms utifrån dispersionsrelationen för materialen (till exempel Debye-modellen ) och Bose–Einstein-statistik . Energi ges helt enkelt av De Broglies våglängdsekvation :

$E\ =\ \hbar \ \omega \left(k\right)\$

var . Den största skillnaden mellan de två modellerna är överföringssannolikheten, vars bestämning är mer komplicerad. I varje fall bestäms det av de grundläggande antaganden som utgör respektive modell. Antagandet om elastisk spridning gör det svårare för fononer att sända över gränssnittet, vilket resulterar i lägre sannolikheter. Som ett resultat representerar den akustiska missanpassningsmodellen typiskt en övre gräns för termiskt gränssnittsmotstånd, medan den diffusa missanpassningsmodellen representerar den nedre gränsen.

Exempel

Gränssnitt för flytande helium

Typisk gränssnittsresistens av flytande helium med metaller. Resistans har multiplicerats med T ³ för att ta bort det förväntade T ⁻³ -beroendet. Anpassad från

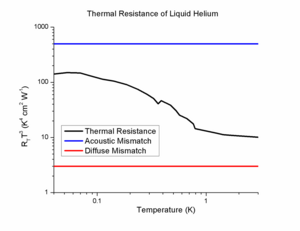
Närvaron av termisk gränssnittsresistans, motsvarande en diskontinuerlig temperatur över ett gränssnitt, föreslogs först från studier av flytande helium 1936. Även om denna idé först föreslogs 1936, var det inte förrän 1941 när Pyotr Kapitsa (Peter Kapitza) genomförde den första systematiska studien av termiskt gränssnittsbeteende i flytande helium. Den första stora modellen för värmeöverföring vid gränssnitt var den akustiska missanpassningsmodellen som förutspådde ett T ^-3 -temperaturberoende på gränsytresistansen, men detta misslyckades med att korrekt modellera den termiska konduktansen för heliumgränssnitt med så mycket som två storleksordningar. Ett annat överraskande beteende hos den termiska resistansen observerades i tryckberoendet . Eftersom ljudets hastighet är en stark funktion av temperaturen i flytande helium, förutsäger den akustiska missanpassningsmodellen ett starkt tryckberoende av gränsytresistansen. Studier runt 1960 visade överraskande nog att gränsytans motstånd var nästan oberoende av tryck, vilket tyder på att andra mekanismer var dominerande.

Den akustiska missanpassningsteorin förutspådde en mycket hög termisk resistans (låg termisk konduktans) vid fast-helium-gränssnitt. Detta är problematiskt för forskare som arbetar vid extremt kalla temperaturer eftersom det kraftigt försvårar nedkylningshastigheter vid låga temperaturer som i utspädningskylskåp. Lyckligtvis observerades inte ett så stort termiskt motstånd på grund av många mekanismer som främjade fonontransport. I flytande helium Van der Waals krafter faktiskt för att stelna de första få monoskikten mot ett fast ämne. Detta gränsskikt fungerar ungefär som en antireflektionsbeläggning i optik, så att fononer som typiskt skulle reflekteras från gränssnittet faktiskt skulle sända över gränssnittet. Detta hjälper också till att förstå tryckoberoendet hos den termiska konduktansen. Den sista dominerande mekanismen för onormalt låg termisk resistans hos flytande heliumgränssnitt är effekten av ytjämnhet , vilket inte tas med i den akustiska missanpassningsmodellen. För en mer detaljerad teoretisk modell av denna aspekt se artikeln av A. Khater och J. Szeftel. Liksom elektromagnetiska vågor som producerar ytplasmoner på grova ytor, kan fononer också inducera ytvågor. När dessa vågor så småningom sprids ger de en annan mekanism för värme att överföra över gränssnittet. På liknande sätt är fononer också kapabla att producera försvinnande vågor i en total intern reflektionsgeometri . Som ett resultat, när dessa vågor sprids i det fasta ämnet, överförs ytterligare värme från heliumet bortom förutsägelsen av teorin om akustisk missanpassning. För en mer fullständig recension om detta ämne, se recensionen av Swartz.

Anmärkningsvärd termisk konduktans vid rumstemperatur

I allmänhet finns det två typer av värmebärare i material: fononer och elektroner. Den fria elektrongasen som finns i metaller är en mycket bra ledare av värme och dominerar värmeledningsförmågan . Alla material uppvisar dock värmeöverföring genom fonontransport så värme flödar även i dielektriska material som kiseldioxid. Värmekonduktans för gränssnitt är ett mått på hur effektivt värmebärare strömmar från ett material till ett annat. Den lägsta termiska konduktansmätningen i rumstemperatur hittills är den Bi/väte-terminerade diamanten med en termisk konduktans på 8,5 MW m ⁻² K ⁻¹ . Som en metall vismut många elektroner som fungerar som de primära värmebärarna. Diamant å andra sidan är en mycket bra elektrisk isolator (även om den har en mycket hög värmeledningsförmåga) och därför är elektrontransporten mellan materialen noll. Vidare har dessa material mycket olika gitterparametrar så att fononer inte effektivt kopplas över gränssnittet. Slutligen Debye-temperaturen mellan materialen väsentligt olika. Som ett resultat har vismut, som har en låg Debye-temperatur, många fononer vid låga frekvenser. Diamant å andra sidan har en mycket hög Debye-temperatur och de flesta av dess värmebärande fononer har frekvenser mycket högre än vad som finns i vismut.

Värmeledningsdata anpassade från,

Ökande i termisk konduktans har de flesta fononmedierade gränssnitten (dielektrisk-dielektrisk och metall-dielektrisk) termiska konduktanser mellan 80 och 300 MW m ⁻² K ⁻¹ . Den största fononmedierade värmeledningsförmågan som hittills uppmätts är mellan TiN (Titanium Nitride) och MgO . Dessa system har mycket liknande gitterstrukturer och Debye-temperaturer. Även om det inte finns några fria elektroner för att förbättra gränsytans termiska konduktans, underlättar de liknande fysiska egenskaperna hos de två kristallerna en mycket effektiv fononöverföring mellan de två materialen.

I den högsta änden av spektrumet är en av de högsta värmeledningsförmågan som uppmätts mellan aluminium och koppar . Vid rumstemperatur har Al-Cu-gränssnittet en konduktans på 4 GW m ⁻² K ⁻¹ . Den höga värmeledningsförmågan hos gränssnittet bör inte vara oväntat med tanke på den höga elektriska ledningsförmågan hos båda materialen.

Gränssnittsresistens i kolnanorör

Den överlägsna värmeledningsförmågan hos nanorör i kol gör det till en utmärkt kandidat för tillverkning av kompositmaterial. Men gränsytresistansen påverkar den effektiva värmeledningsförmågan. Detta område är inte väl studerat och endast ett fåtal studier har gjorts för att förstå den grundläggande mekanismen för denna resistens.