Taylor–von Neumann–Sedov explosionsvåg

Taylor–von Neumann–Sedov sprängvåg (eller ibland kallad Sedov–von Neumann–Taylor sprängvåg ) hänvisar till en sprängvåg inducerad av en kraftig explosion. Sprängvågen beskrevs av en självliknande lösning oberoende av GI Taylor , John von Neumann och Leonid Sedov under andra världskriget .

Historia

GI Taylor fick höra av det brittiska inrikesministeriet att det skulle vara möjligt att producera en bomb där en mycket stor mängd energi skulle frigöras genom kärnklyvning och ombads att rapportera effekten av sådana vapen. Taylor presenterade sina resultat den 27 juni 1941. Exakt samtidigt, i USA , arbetade John von Neumann med samma problem och han presenterade sina resultat den 30 juni 1941. Det sades att Leonid Sedov också arbetade om problemet ungefär samtidigt i Sovjetunionen , även om Sedov aldrig bekräftade några exakta datum.

Den kompletta lösningen publicerades först av Sedov 1946. von Neumann publicerade sina resultat i augusti 1947 i Los Alamos vetenskapliga laboratorierapport om " Blast wave" (PDF) . Arkiverad (PDF) från originalet den 1 juni 2022. , även om rapporten distribuerades först 1958. Taylor fick tillstånd att publicera sina resultat 1949 och han publicerade sina verk i två tidningar 1950. I den andra tidningen beräknade Taylor energin från atombomben som användes i Treenigheten (kärnprov) med hjälp av likheten, bara genom att titta på serien av explosionsvågfotografier som hade en längdskala och tidsstämplar, publicerade av Julian E Mack 1947. Denna energiberäkning orsakade , med Taylors egna ord, "mycket pinsamt" (enligt Grigory Barenblatt ) i amerikanska regeringskretsar eftersom siffran då fortfarande var hemligstämplad även om fotografierna som publicerats av Mack inte var det. Taylors biograf George Batchelor skriver . Denna uppskattning av utbytet av den första atombombexplosionen orsakade en hel del uppståndelse... GI blev milt förmanad av den amerikanska armén för att ha publicerat sina avdrag från deras (oklassificerade) fotografier .

Matematisk beskrivning

Tänk på en kraftig explosion (som kärnvapenbomber) som frigör en stor mängd energi $E$ i en liten volym under ett kort tidsintervall. Detta kommer att skapa en stark sfärisk stötvåg som fortplantar sig utåt från explosionscentrumet. Den självliknande lösningen försöker beskriva flödet när stötvågen har rört sig över en sträcka som är extremt stor jämfört med storleken på sprängämnet. På dessa stora avstånd kommer informationen om explosionens storlek och varaktighet att glömmas bort; endast den energi som frigörs $E$ kommer att ha inflytande på hur stötvågen utvecklas. Till en mycket hög grad av noggrannhet kan det antas att explosionen inträffade vid en punkt (säg origo $r=0$ ) momentant vid tidpunkten $t=0$ .

Stötvågen i det självliknande området antas fortfarande vara mycket stark så att trycket bakom chockvågen $p_{1}$ är mycket stort i jämförelse med trycket (atmosfärstrycket) framför stötvåg $p_{0}$ , som kan försummas från analysen. Även om trycket för den ostörda gasen är försumbart, kan densiteten hos den ostörda gasen $\rho _{0}$ inte försummas eftersom täthetshoppet över starka stötvågor är ändligt som en direkt konsekvens av Rankine-Hugoniot-förhållandena . Denna approximation är ekvivalent med inställningen $p_{0}=0$ och motsvarande ljudhastighet $c_{0}=0$ , men att hålla sin densitet icke noll, dvs. $\rho _{0}\neq 0$ .

De enda tillgängliga parametrarna till vårt förfogande är energin $E$ och den ostörda gasdensiteten $\rho _{0}$ . Egenskaperna bakom stötvågen som $p_{1},\,\rho _{1}$ är härledbara från de som ligger framför stötvågen. Den enda icke-dimensionella kombinationen som är tillgänglig från $r,\,t,\,\rho _{0}$ och $E$ är

{\displaystyle r\left({\frac {\rho _{0}}{Et^{2}}}\right)^{1/5

.

Det är rimligt att anta att utvecklingen i $r$ och $t$ för stötvågen endast beror på variabeln ovan. Detta betyder att chockvågsplatsen $r=R(t)$ själv kommer att motsvara ett visst värde, säg $\beta$ , för denna variabel, dvs.

R=\beta \left({\frac {Et^{2}}{\rho _{0}}}\right)^{1/5}.

Utbredningshastigheten för stötvågen är

D={\frac {\mathrm {d} R}{\mathrm {d} t}}= {\frac {2R}{5t}}={\frac {2\beta }{5}}\left({\frac {E}{\rho _{0}t^{3}}}\right)^ {1/5}

Med den approximation som beskrivs ovan bestämmer Rankine–Hugoniot-förhållanden gashastigheten omedelbart bakom stötfronten $v_{1}$ , $p_{1}$ och $\rho _{ 1}$ för en idealisk gas enligt följande

v_{1}={\frac {2}{\gamma +1} }D,\quad p_{1}={\frac {2}{\gamma +1}}\rho _{0}D^{2},\quad \rho _{1}=\rho _{0} {\frac {\gamma +1}{\gamma -1}}

där $\gamma$ är det specifika värmeförhållandet . Eftersom $\rho _{0}$ är en konstant, förändras inte densiteten omedelbart bakom stötvågen med tiden, medan $v_{1}$ och $p_{1}$ minska som $t^{-3/5}$ respektive $t^{-6/5}$ .

Självliknande lösning

Gasrörelsen bakom stötvågen styrs av Eulers ekvationer . För en idealisk polytrop $\rho (r ,t)$ med sfärisk symmetri, ekvationerna för vätskevariablerna såsom radiell hastighet $v(r,t)$ , densitet och tryck $p(r,t)$ ges av

{\begin{aligned}{\frac {\partial v}{\partial t}}+v{\frac {\partial v}{\partial r}}&=-{\ frac {1}{\rho }}{\frac {\partial p}{\partial r}},\\{\frac {\partial \rho }{\partial t}}+{\frac {\partial (\ rho v)}{\partial r}}&=-{\frac {2\rho v}{r}},\\\left({\frac {\partial }{\partial t}}+v{\frac {\partial }{\partial r}}\right)\ln {\frac {p}{\rho ^{\gamma }}}&=0.\end{aligned}}

Vid $r=R(t)$ bör lösningarna närma sig de värden som ges av Rankine-Hugoniot-villkoren definierade i föregående avsnitt.

Det variabla trycket kan ersättas med ljudhastigheten $c(r,t)$ eftersom trycket kan erhållas från formeln $c^{2}= \gamma p/\rho$ . Följande icke-dimensionella självliknande variabler introduceras,

\xi ={\frac { r}{R(t)}},\quad V(\xi )={\frac {5tv}{2r}},\quad G(\xi )={\frac {\rho }{\rho _{0 }}},\quad Z(\xi )={\frac {25t^{2}c^{2}}{4r^{2}}}

.

Villkoren vid stötdämparens front $\xi =1$ blir

V(1)={\frac {2}{\gamma +1}},\quad G(1)={\frac {\gamma +1}{\gamma -1}},\quad Z( 1)={\frac {2\gamma (\gamma -1)}{(\gamma +1)^{2}}}.

Att ersätta de självliknande variablerna i de styrande ekvationerna kommer att leda till tre vanliga differentialekvationer. Att lösa dessa differentialekvationer analytiskt är mödosamt, vilket visades av Sedov 1946 och von Neumann 1947. GI Taylor integrerade dessa ekvationer numeriskt för att få önskade resultat.

Relationen mellan $Z$ och $V$ kan härledas direkt från energibesparing. Eftersom energin associerad med den ostörda gasen försummas genom att sätta $p_{0}=0$ , måste den totala energin för gasen inom stötsfären vara lika med $E$ . På grund av självlikhet är det tydligt att inte bara den totala energin inom en sfär med radie $\xi =1$ är konstant, utan också den totala energin inom en sfär med valfri radie ${\ displaystyle \xi <1}$ (i dimensionell form står det att total energi inom en sfär med radie $r$ som rör sig utåt med en hastighet $v_{n}=2r /5t$ måste vara konstant). Mängden energi som lämnar sfären med radie $r$ i tiden $dt$ på grund av gashastigheten $v$ är ${\displaystyle 4\pi r^{2}\rho v(h+v^{2}/2)\mathrm {d} t} , där$ h $\displaystyle h}$ är gasens specifika entalpi . Under den tiden ökar sfärens radie med hastigheten $v_{n}$ och gasens energi i denna extra ökade volym är ${\displaystyle 4\pi r^{2}\rho v_{n}(e+v^{2}/2)\mathrm {d} t} , där e {\displaystyle e$ } $den$ specifika energin för gasen. Att likställa dessa uttryck och ersätta $e=c^{2}/\gamma (\gamma -1)$ och $h=c^{2}/(\gamma -1)$ som är giltig för ideal polytropisk gas leder till

Z={\frac {\gamma (\gamma -1)(1-V)V^{2}}{2(\gamma V-1)}}.

Kontinuitets- och energiekvationen minskar till

{\begin{aligned}{\frac {\mathrm {d} V}{\mathrm {d} \ln \xi }}-(1-V){\frac {\mathrm {d} \ln G }{\mathrm {d} \ln \xi }}&=-3V\\{\frac {\mathrm {d} \ln Z}{\mathrm {d} \ln \xi }}-(\gamma -1 ){\frac {\mathrm {d} \ln G}{\mathrm {d} \ln \xi }}&=-{\frac {5-2V}{1-V}}.\end{aligned}}

Självliknande lösning av Taylor-von Neumann-Sedov sprängvåg för

\displaystyle \gamma =7/5

Uttrycka $\mathrm {d} V/\mathrm {d} \ln \xi$ och $\mathrm {d} \ln G/\mathrm {d} V$ som en funktion av $V$ endast genom att använda den tidigare erhållna relationen och integrera en gång ger lösningen i implicit form,

{\begin{aligned}\xi ^{5}&=\left[{\frac {1}{2}}(\gamma +1)V\ höger]^{-2}\left\{{\frac {\gamma +1}{7-\gamma }}[5-(3\gamma -1)V]\right\}^{\nu _{1 }}\vänster[{\frac {\gamma +1}{\gamma -1}}(\gamma V-1)\höger]^{\nu _{2}},\\G&={\frac {\ gamma +1}{\gamma -1}}\vänster[{\frac {\gamma +1}{\gamma -1}}(\gamma V-1)\höger]^{\nu _{3}}\ vänster\{{\frac {\gamma +1}{7-\gamma }}[5-(3\gamma -1)V\right\}^{\nu _{4}}\left[{\frac { \gamma +1}{\gamma -1}}(1-V)\right]^{\nu _{5}}\end{aligned}}

var

\nu _{1}=-{\frac {13\gamma ^{2}-7\gamma +12}{(3\gamma -1)(2\gamma +1)}},\quad \ nu _{2}={\frac {5(\gamma -1)}{2\gamma +1}},\quad \nu _{3}={\frac {3}{2\gamma +1}} ,\quad \nu _{4}=-{\frac {\nu _{1}}{2-\gamma }},\quad \nu _{5}=-{\frac {2}{2-\ gamma }}.

Konstanten $\beta$ som bestämmer chockplatsen kan bestämmas utifrån bevarande av energi

E=\int _{0}^{R}\rho [v^{2} /2+c^{2}/\gamma (\gamma -1)]4\pi r^{2}\mathrm {d} r

för att uppnå

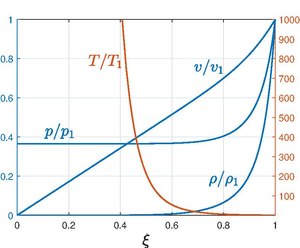
\beta ^{5}{\frac {16\pi }{25} }\int _{0}^{1}G[V^{2}/2+Z/\gamma (\gamma -1)]\xi ^{4}\mathrm {d} \xi =1.

För luft är $\gamma =7/5$ och $1,033}$ . Lösningen för $\gamma =7/5$ visas i figuren genom att plotta kurvorna för $\rho /\rho _{1}=G(\gamma -1)/(\gamma +1)$ , $v/v_{1}=\xi V(\gamma +1)/2$ , $p/p_{1}=\xi ^{2}GZ(\gamma +1)/(2\gamma )$ och $T/T_{1}=\xi ^{ 2}Z(\gamma +1)^{2}/[2\gamma (\gamma -1)],$ där $T$ är temperaturen.

Asymptotiskt beteende nära den centrala regionen

Det asymptotiska beteendet i den centrala regionen kan undersökas genom att ta gränsen $\xi \rightarrow 0$ . Från figuren kan det observeras att densiteten faller till noll mycket snabbt bakom stötvågen. Hela massan av gasen som till en början spreds jämnt ut i en sfär med radien $R$ finns nu i ett tunt lager bakom stötvågen, det vill säga all massa drivs utåt av den acceleration som ges av chockvågen. Därmed är större delen av regionen i princip tom. Tryckförhållandet sjunker också snabbt för att uppnå det konstanta värdet $p_{c}$ . Temperaturförhållandet följer av den ideala gaslagen; eftersom densitetsförhållandet sjunker till noll och tryckförhållandet är konstant måste temperaturförhållandet bli oändligt. Den begränsande formen för densiteten ges enligt följande

\displaystyle {\frac {\rho }{\ rho _{1}}}\sim \xi ^{3/(\gamma -1)},\quad {\frac {p}{p_{1}}}\högerpil p_{c},\quad {\frac {T}{T_{1}}}\sim \xi ^{-3/(\gamma -1)}\quad {\text{as}}\quad \xi \rightarrow 0.}

Kom ihåg att densiteten $\rho _{1}$ är tidsoberoende medan $p_{1}\sim t^{-6/5}$ vilket betyder att det faktiska trycket är i själva verket tidsberoende. Det blir tydligt om ovanstående former skrivs om i dimensionella enheter,

\rho \sim r^{3/(\gamma -1)}t^{-6/5(\gamma -1)},\quad p\rightarrow p_{c}t^{-6/5},\quad T\sim r^{-3/(\gamma -1)}t^{(6/5)(2-\gamma )/( \gamma -1)}\quad {\text{as}}\quad r\rightarrow 0.

Hastighetsförhållandet har det linjära beteendet i den centrala regionen,

{\frac {v}{v_{1}}}\sim \xi \quad {\text{as}}\quad \xi \rightarrow 0

medan själva hastighetens beteende ges av

v\sim rt^{1/5}\quad {\text{as}}\quad r\rightarrow 0.

Slutskedet av sprängvågen

När stötvågen utvecklas med tiden minskar dess styrka. Den självliknande lösningen som beskrivs ovan går sönder när $p_{1}$ blir jämförbar med $p_{0}$ (mer exakt, när $p_{1}\sim [(\gamma +1)/(\gamma -1)]p_{0}$ ). I detta senare skede av utvecklingen kan $p_{0}$ (och följaktligen $c_{0}$ ) inte försummas. Detta betyder att utvecklingen inte är sig själv lik, eftersom man kan bilda en längdskala $(E/p_{0})^{1/3}$ och en tidsskala $(E/p_{0})^{1/3}/c_{0}$ för att beskriva problemet. De styrande ekvationerna integreras sedan numeriskt, vilket gjordes av H. Goldstine och John von Neumann , Brode och Okhotsimskii et al.

Cylindrisk linjeexplosion

Det analoga problemet inom cylindrisk geometri som motsvarar en axisymmetrisk sprängvåg kan lösas analytiskt. Detta problem löstes oberoende av Leonid Sedov , A. Sakurai och SC Lin.

Se även