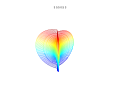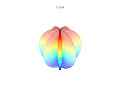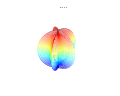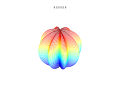Superformel

Superformeln är en generalisering av superellipsen och föreslogs av Johan Gielis omkring 2000. Gielis föreslog att formeln kan användas för att beskriva många komplexa former och kurvor som finns i naturen . Gielis har lämnat in en patentansökan relaterad till syntesen av mönster som genereras av superformeln, som löpte ut från och med 2020-05-10.

I polära koordinater , med $r$ radien och $\varphi$ vinkeln, är superformeln:

r\left(\varphi \right)=\left(\left|{\frac {\cos \left({\frac {m\varphi }{4}}\right)}{a}}\right |^{n_{2}}+\left|{\frac {\sin \left({\frac {m\varphi }{4}}\right)}{b}}\right|^{n_{3} }\right)^{-{\frac {1}{n_{1}}}}.

Genom att välja olika värden för parametrarna $a,b,m,n_{1},n_{2},$ och $n_{3} ,$ olika former kan genereras.

Formeln erhölls genom att generalisera superellipsen, namngiven och populariserad av Piet Hein , en dansk matematiker .

2D plots

I följande exempel ska värdena som visas ovanför varje figur vara m , n ₁ , n ₂ och n ₃ .

Ett GNU Octave- program för att generera dessa figurer

 
    0  
                          
         
      
      
   
 funktion  sf2d  (  n, a  )  u  =  [  :  .001  :  2  *  pi  ];  raux  =  abs  (  1  /  a  (  1  )  .*  abs  (  cos  (  n  (  1  )  *  u  /  4  )))  .^  n  (  3  )  +  abs  (  1  /  a  (  2  )  .*  abs  (  sin  (  n  ( )  1  )  *  u  /  4  )))  .^  n  (  4  );  r  =  abs  (  raux  )  .  ^  (  -1  /  n  (  2  ));  x  =  r  .*  cos  (  u  );  y  =  r  .*  sin  (  u  );  plot  (  x  ,  y  );  slutet

Förlängning till högre dimensioner

Det är möjligt att utöka formeln till 3, 4 eller n dimensioner med hjälp av den sfäriska produkten av superformler. Till exempel erhålls den 3D- parametriska ytan genom att multiplicera två superformler r ₁ och r ₂ . Koordinaterna definieras av relationerna:

x=r_{1}(\theta )\cos \theta \cdot r_{2}(\phi )\cos \ phi ,

y=r_{1}(\theta )\sin \theta \cdot r_{2}(\phi ) \cos \phi ,

z=r_{2}(\phi )\sin \phi ,

där $\phi$ ( latitud ) varierar mellan − π /2 och π /2 och θ ( longitud ) mellan − π och π .

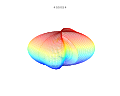
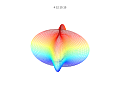
3D-plots

3D-superformel: a = b = 1; m , n ₁ , n ₂ och n ₃ visas på bilderna.

Ett GNU Octave -program för att generera dessa figurer:

 
     
         
    
    
     
       
                              
             
                              
             
               
               
           
    
  
    
 funktion  sf3d  (  n, a  )  u  =  [  -pi  :  .05  :  pi  ]  ;  v  =  [  -pi  /  2  :  .05  :  pi  /  2  ]  ;  nu  =  längd  (  u  );  nv  =  längd  (  v  );  för  i  =  1  :  nu  för  j  =  1  :  nv  raux1  =  abs  (  1  /  a  (  1  )  *  abs  (  cos  (  n  (  1  )  .*  u  (  i  )  /  4  )))  .^  n  (  3  )  +  abs  (  1  /  a  (  2  )  *  abs  (  sin  (  n  (  1  )  *  u  (  i  )  /  4  )))  .^  n  (  4  );  r1  =  abs  (  raux1  )  .^  (-1  /  n  (  2  )  )  ;  raux2  =  abs  (  1  /  a  (  1  )  *  abs  (  cos  (  n  (  1  )  *  v  (  j  )  /  4  )))  .^  n  (  3  )  +  abs  (  1  /  a  (  2  )  *  abs  (  sin  (  n )  (  1  )  *  v  (  j  )  /  4  )))  .^  n  (  4  );  r2  =  abs  (  raux2  )  .^  (  -1  /  n  (  2  ))  ;  x  (  i  ,  j  )  =  rl  *  cos  (  u  (  i  ))  *  r2  *  cos  (  v  (  j  ));  y  (  i  ,  j  )  =  r1  *  sin  (  u  (  i  ))  *  r2  *  cos  (  v  (  j  ));  z  (  i  ,  j  )  =  r2  *  sin  (  v  (  j  ));  endfor  ;  endfor  ;  mesh  (  x  ,  y  ,  z  );  slutfunktion  ;

Generalisering

Superformeln kan generaliseras genom att tillåta distinkta m parametrar i superformelns två termer. Genom att ersätta den första parametern $m$ med y och den andra parametern $m$ med z :

r\left(\varphi \right)=\ left(\left|{\frac {\cos \left({\frac {y\varphi }{4}}\right)}{a}}\right|^{n_{2}}+\left|{\ frac {\sin \left({\frac {z\varphi}{4}}\right)}{b}}\right|^{n_{3}}\right)^{-{\frac {1}{ n_{1}}}}

Detta möjliggör skapandet av rotationsasymmetriska och kapslade strukturer. I följande exempel är a, b, ${n_{2}}$ och ${n_{3}}$ 1:

externa länkar