Strassen algoritm

Ej att förväxla med Schönhage–Strassen-algoritmen för multiplikation av polynom.

Inom linjär algebra är Strassen -algoritmen , uppkallad efter Volker Strassen , en algoritm för matrismultiplikation . Den är snabbare än standardmatrismultiplikationsalgoritmen för stora matriser, med en bättre asymptotisk komplexitet, även om den naiva algoritmen ofta är bättre för mindre matriser. Strassen-algoritmen är långsammare än de snabbaste kända algoritmerna för extremt stora matriser, men sådana galaktiska algoritmer är inte användbara i praktiken, eftersom de är mycket långsammare för matriser av praktisk storlek. För små matriser finns det ännu snabbare algoritmer.

Strassens algoritm fungerar för vilken ring som helst , som plus/multiplikera, men inte alla semiringar , som min-plus eller boolesk algebra , där den naiva algoritmen fortfarande fungerar, och så kallad kombinatorisk matrismultiplikation.

Historia

Volker Strassen publicerade denna algoritm först 1969 och bevisade därmed att $n^{3}$ generella matrismultiplikationsalgoritmen inte var optimal. Strassen-algoritmens publicering resulterade i mer forskning om matrismultiplikation som ledde till både asymptotiskt lägre gränser och förbättrade beräkningsmässiga övre gränser.

Algoritm

Den vänstra kolumnen visualiserar de beräkningar som krävs för att bestämma resultatet av en 2x2 matrismultiplikation . Naiv matrismultiplikation kräver en multiplikation för varje "1" i den vänstra kolumnen. Var och en av de andra kolumnerna (M1-M7) representerar en enda av de 7 multiplikationerna i Strassen-algoritmen. Summan av kolumnerna M1-M7 ger samma resultat som fullmatrismultiplikationen till vänster.

Låt $A$ , $B$ vara två kvadratiska matriser över en ring ${\mathcal {R}}$ , till exempel matriser vars poster är heltal eller de reella talen. Målet med matrismultiplikation är att beräkna matrisprodukten $C=AB$ . Följande beskrivning av algoritmen antar att alla dessa matriser har storlekar som är två potenser (dvs. ${\displaystyle A,\,B,\,C \in \operatorname {Matr} _{2^{n}\times 2^{n}}({\mathcal {R}})} ), men detta är endast begreppsmässigt nödvändigt -- om matriserna$ A $\displaystyle A }$ , $B$ är inte av typen $2^{n}\times 2^{n}$ , de "saknade" raderna och kolumnerna kan fyllas med nollor för att få matriser med storlekar av två potenser -- även om verkliga implementeringar av algoritmen inte gör detta i praktiken.

Strassen-algoritmen delar upp $A$ , $B$ och $C$ i lika stora blockmatriser

$A={\begin{bmatrix} A_{11}&A_{12}\\A_{21}&A_{22}\end{bmatrix}},\quad B={\begin{bmatrix}B_{11}&B_{12}\\B_{21}&B_ {22}\end{bmatrix}},\quad C={\begin{bmatrix}C_{11}&C_{12}\\C_{21}&C_{22}\end{bmatrix}},\quad$

med $A_{ij},B_{ij},C_{ij}\in \operatorname {Mat } _{2^{n-1}\ gånger 2^{n-1}}({\mathcal {R}})$ . Den naiva algoritmen skulle vara:

${\begin{bmatrix}C_{11}&C_{12}\\C_{21}&C_{22}\end{bmatrix}}={\begin{bmatrix}A_{11}B_{11}+A_ {12}B_{21}&A_{11}B_{12}+A_{12}B_{22}\\A_{21}B_{11}+A_{22}B_{21}&A_{21}B_{12 }+A_{22}B_{22}\end{bmatrix}}.$

Denna konstruktion minskar inte antalet multiplikationer: 8 multiplikationer av matrisblock behövs fortfarande för att beräkna ${\displaystyle C_{ij}}-$ matriserna, samma antal multiplikationer som behövs när man använder standardmatrismultiplikation.

Strassen-algoritmen definierar istället nya matriser:

${\begin{aligned}M_{1}&=(A_{11}+A_{22})(B_{11}+ B_{22});\\M_{2}&=(A_{21}+A_{22})B_{11};\\M_{3}&=A_{11}(B_{12}-B_{ 22});\\M_{4}&=A_{22}(B_{21}-B_{11});\\M_{5}&=(A_{11}+A_{12})B_{22 };\\M_{6}&=(A_{21}-A_{11})(B_{11}+B_{12});\\M_{7}&=(A_{12}-A_{22 })(B_{21}+B_{22}),\\\end{aligned}}$

använder endast 7 multiplikationer (en för varje $M_{k}$ ) istället för 8. Vi kan nu uttrycka $C_{ij}$ i termer av $M_{k }$ :

${\begin{bmatrix}C_{11}&C_{12}\\C_{21}&C_{22}\end{bmatrix}}={\begin{bmatrix}M_{1}+M_{4}- M_{5}+M_{7}&M_{3}+M_{5}\\M_{2}+M_{4}&M_{1}-M_{2}+M_{3}+M_{6}\end {bmatrix}}.$

Vi upprepar denna divisionsprocess rekursivt tills submatriserna degenererar till tal (element i ringen ${\displaystyle {\mathcal {R}}} )$ . Om, som nämnts ovan, den ursprungliga matrisen hade en storlek som inte var en potens av 2, så kommer den resulterande produkten att ha noll rader och kolumner precis som $A$ och $B$ , och dessa kommer då att tas bort vid denna tidpunkt för att få den (mindre) matris $C$ vi verkligen ville ha.

Praktiska implementeringar av Strassens algoritm byter till standardmetoder för matrismultiplikation för tillräckligt små submatriser, för vilka dessa algoritmer är mer effektiva. Den särskilda övergångspunkten för vilken Strassens algoritm är mer effektiv beror på den specifika implementeringen och hårdvaran. Tidigare författare hade uppskattat att Strassens algoritm är snabbare för matriser med bredder från 32 till 128 för optimerade implementeringar. Det har dock observerats att denna övergångspunkt har ökat under de senaste åren, och en studie från 2010 fann att även ett enda steg av Strassens algoritm ofta inte är fördelaktigt på nuvarande arkitekturer, jämfört med en mycket optimerad traditionell multiplikation, tills matrisstorlekarna överskrider 1000 eller mer, och även för matrisstorlekar på flera tusen är fördelen vanligtvis marginell i bästa fall (cirka 10 % eller mindre). En nyare studie (2016) observerade fördelar för matriser så små som 512 och en fördel runt 20 %.

Winograd form

Det är möjligt att minska antalet matristillägg genom att istället använda följande form som upptäckts av Winograd:

${\begin{bmatrix}a&b\\c&d\end{bmatrix}}{\begin{bmatrix}A&C\\B&D\end{bmatrix}}={\begin{bmatrix}aA+bB&w+v+ (a+bcd)D\\w+u+d(B+CAD)&w+u+v\end{bmatrix}}$

där u = (c - a) (C - D), v = (c + d) (C - A), w = aA + (c + d - a) (A + D - C). Detta minskar antalet matrisadditioner och subtraktioner från 18 till 15. Antalet matrismultiplikationer är fortfarande 7, och den asymptotiska komplexiteten är densamma.

Asymptotisk komplexitet

Översikten av algoritmen ovan visade att man kan komma undan med bara 7, istället för de traditionella 8, matris-matris-multiplikationer för sub-blocken av matrisen. Å andra sidan måste man göra additioner och subtraktioner av block, även om detta inte är av betydelse för den övergripande komplexiteten: Att lägga till matriser av storlek $N/2$ kräver endast ${\ displaystyle (N/2)^{2}}$ operationer medan multiplikation är betydligt dyrare (traditionellt $2(N/2)^{3}$ additions- eller multiplikationsoperationer).

Frågan är då hur många operationer man behöver för Strassens algoritmer, och hur detta jämförs med standardmatrismultiplikationen som tar ungefär $2N^{3}$ (där $N=2 ^{n}$ ) aritmetiska operationer, dvs en asymptotisk komplexitet $\Theta (N^{3})$ .

Antalet additioner och multiplikationer som krävs i Strassen-algoritmen kan beräknas enligt följande: låt $f(n)$ vara antalet operationer för en $2^{n} \times 2^{n}$ matris. Sedan genom rekursiv tillämpning av Strassen-algoritmen ser vi att $f(n)=7f(n-1)+l4^{n}$ , för någon konstant $l$ som beror på antalet tillägg som utförs vid varje tillämpning av algoritmen. Därför ${\displaystyle f(n)=(7+o(1))^{n}} ,$ dvs den asymptotiska komplexiteten för multiplicering av matriser med storlek $N=2^{n}$ som använder Strassen-algoritmen är ${ \displaystyle O([7+o(1)]^{n})=O(N^{\log _{2}7+o(1)})\approx O(N^{2.8074})}$ . Minskningen av antalet aritmetiska operationer kommer dock till priset av en något minskad numerisk stabilitet , och algoritmen kräver också betydligt mer minne jämfört med den naiva algoritmen. Båda initialmatriserna måste ha sina dimensioner expanderade till nästa potens av 2, vilket resulterar i att man lagrar upp till fyra gånger så många element, och de sju hjälpmatriserna innehåller vardera en fjärdedel av elementen i de expanderade.

Strassens algoritm måste jämföras med det "naiva" sättet att göra matrismultiplikationen som skulle kräva 8 istället för 7 multiplikationer av delblock. Detta skulle då ge upphov till den komplexitet man förväntar sig av standardmetoden: $O(8^{\log _{ 2}n})=O(N^{\log _{2}8})=O(N^{3})$ . Jämförelsen av dessa två algoritmer visar att asymptotiskt är Strassens algoritm snabbare: Det finns en storlek $N_{\text{threshold}}$ så att matriser som är större multipliceras mer effektivt med Strassens algoritm än den "traditionella " sätt. Det asymptotiska påståendet innebär dock inte att Strassens algoritm alltid är snabbare även för små matriser, och i praktiken är detta faktiskt inte fallet: För små matriser överväger kostnaden för ytterligare tillägg av matrisblock besparingarna i antalet multiplikationer. Det finns också andra faktorer som inte fångas upp av analysen ovan, såsom skillnaden i kostnad på dagens hårdvara mellan att ladda data från minnet till processorer kontra kostnaden för att faktiskt utföra operationer på denna data. Som en konsekvens av dessa typer av överväganden används Strassens algoritm vanligtvis bara på "stora" matriser. Denna typ av effekt är ännu mer uttalad med alternativa algoritmer som den av Coppersmith och Winograd : Även om den är asymptotiskt ännu snabbare, är övergångspunkten $N_{\text{threshold}}$ så stor att algoritmen används i allmänhet inte på matriser man möter i praktiken.

Rang eller bilinär komplexitet

Den bilinjära komplexiteten eller rangordningen för en bilinjär karta är ett viktigt begrepp i den asymptotiska komplexiteten av matrismultiplikation. Rangen för en bilinjär karta $\phi :\mathbf {A} \times \mathbf {B} \rightarrow \mathbf {C}$ över ett fält F definieras som (något av en missbruk av notation )

$R(\phi /\mathbf {F} )=\min \left\{r\left|\exists f_{i}\in \mathbf {A} ^{*},g_{i}\ i \mathbf {B} ^{*},w_{i}\in \mathbf {C} ,\forall \mathbf {a} \in \mathbf {A} ,\mathbf {b} \in \mathbf {B} ,\phi (\mathbf {a} ,\mathbf {b} )=\sum _{i=1}^{r}f_{i}(\mathbf {a} )g_{i}(\mathbf {b} )w_{i}\right.\right\}$

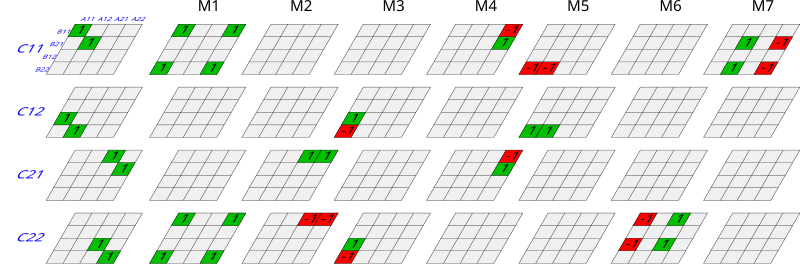
Med andra ord är rangordningen för en bilinjär karta längden på dess kortaste bilinjära beräkning. Förekomsten av Strassens algoritm visar att rangordningen för $2\times 2$ matrismultiplikation inte är mer än sju. För att se detta, låt oss uttrycka denna algoritm (vid sidan av standardalgoritmen) som en sådan bilinjär beräkning. När det gäller matriser består de dubbla utrymmena A * och B * av kartor in i fältet F inducerade av en skalär dubbelpunktsprodukt , (dvs i detta fall summan av alla poster i en Hadamard-produkt .)

	Standardalgoritm				Strassen algoritm
$i$	$f_{i}(\mathbf {a} )$	$g_{i}(\mathbf {b} )$	$w_{i}$		$f_{i}(\mathbf {a})$	$g_{i}(\mathbf {b} )$	$w_{i}$
1	${\begin{bmatrix}1&0\\0&0\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}1&0\\0&0\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}1&0\\0&0\end{bmatrix}}$		${\begin{bmatrix}1&0\\0&1\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}1&0\\0&1\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}1&0\\0&1\end{bmatrix}}$
2	${\begin{bmatrix}0&1\\0&0\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}0&0\\1&0\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}1&0\\0&0\end{bmatrix}}$		${\begin{bmatrix}0&0\\1&1\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}1&0\\0&0\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}0&0\\1&-1\end{bmatrix}}$
3	${\begin{bmatrix}1&0\\0&0\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}0&1\\0&0\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}0&1\\0&0\end{bmatrix}}$		${\begin{bmatrix}1&0\\0&0\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}0&1\\0&-1\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}0&1\\0&1\end{bmatrix}}$
4	${\begin{bmatrix}0&1\\0&0\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}0&0\\0&1\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}0&1\\0&0\end{bmatrix}}$		${\begin{bmatrix}0&0\\0&1\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}-1&0\\1&0\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}1&0\\1&0\end{bmatrix}}$
5	${\begin{bmatrix}0&0\\1&0\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}1&0\\0&0\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}0&0\\1&0\end{bmatrix}}$		${\begin{bmatrix}1&1\\0&0\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}0&0\\0&1\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}-1&1\\0&0\end{bmatrix}}$
6	${\begin{bmatrix}0&0\\0&1\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}0&0\\1&0\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}0&0\\1&0\end{bmatrix}}$		${\begin{bmatrix}-1&0\\1&0\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}1&1\\0&0\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}0&0\\0&1\end{bmatrix}}$
7	${\begin{bmatrix}0&0\\1&0\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}0&1\\0&0\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}0&0\\0&1\end{bmatrix}}$		${\begin{bmatrix}0&1\\0&-1\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}0&0\\1&1\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}1&0\\0&0\end{bmatrix}}$
8	${\begin{bmatrix}0&0\\0&1\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}0&0\\0&1\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}0&0\\0&1\end{bmatrix}}$
	$\mathbf {a} \mathbf {b} =\sum _{i=1}^{8}f_{i} (\mathbf {a} )g_{i}(\mathbf {b} )w_{i}$				$\mathbf {a} \mathbf {b} =\sum _{i=1}^{7}f_{i} (\mathbf {a} )g_{i}(\mathbf {b} )w_{i}$

Det kan visas att det totala antalet elementära multiplikationer $L$ som krävs för matrismultiplikation är tätt asymptotiskt bundet till rangordningen $R$ , dvs $L=\Theta ( R)$ , eller mer specifikt, eftersom konstanterna är kända, $R/2\leq L\leq R$ . En användbar egenskap hos rangordningen är att den är submultiplikativ för tensorprodukter , och detta gör det möjligt att visa att $2^{n}\times 2^{n}\times 2^{ n}$ matrismultiplikation kan åstadkommas med högst $7n$ elementära multiplikationer för alla $n$ . (Denna $n$ -faldiga tensorprodukten av $2\times 2\times 2$ -matrismultiplikationskartan med sig själv — en ${\displaystyle n} -$ :e tensorpotentialen — realiseras genom det rekursiva steget i den visade algoritmen.)

Cachebeteende

Strassens algoritm är cache-omedveten . Analys av dess cache- beteendealgoritm har visat att det uppstår

$\Theta \left(1+{\frac {n^{2}}{b}}+{\frac {n^{\log _{2}7}}{b{\sqrt {M}}}}\right)$

cache missar under dess exekvering, förutsatt att en idealiserad cache av storlek $M$ (dvs. med $M/b$ rader med längden $b$ ).

Implementeringsöverväganden

Beskrivningen ovan anger att matriserna är kvadratiska och storleken är en potens av två, och att stoppning ska användas om det behövs. Denna begränsning tillåter att matriserna delas på mitten, rekursivt, tills gränsen för skalär multiplikation nås. Begränsningen förenklar förklaringen och analysen av komplexitet, men är faktiskt inte nödvändig; och i själva verket kommer utfyllnad av matrisen enligt beskrivning att öka beräkningstiden och kan enkelt eliminera de ganska snäva tidsbesparingar som erhålls genom att använda metoden i första hand.

En bra implementering kommer att observera följande:

• Det är inte nödvändigt eller önskvärt att använda Strassen-algoritmen ner till gränsen för skalärer. Jämfört med konventionell matrismultiplikation, adderar algoritmen en avsevärd $O(n^{2})$ arbetsbelastning i addition/subtraktion; så under en viss storlek är det bättre att använda konventionell multiplikation. Således behöver till exempel en $1600\times 1600$ inte utfyllas till $2048\times 2048$ eftersom den skulle kunna delas upp till $2048\times 2048} \times 25$ matriser och konventionell multiplikation kan sedan användas på den nivån.
• Metoden kan verkligen tillämpas på kvadratiska matriser av vilken dimension som helst. Om måtten är jämn delas de på mitten enligt beskrivningen. Om dimensionen är udda tillämpas nollutfyllnad med en rad och en kolumn först. Sådan stoppning kan appliceras på-the-fly och lättjefullt, och de extra raderna och kolumnerna kasseras när resultatet bildas. Anta till exempel att matriserna är $199\times 199$ . De kan delas så att den övre vänstra delen är $100\times 100$ och den nedre högra delen är $99\times 99$ . Varhelst operationerna kräver det, är dimensionerna $99$ nollutfyllda till $100$ först. Notera till exempel att produkten $M_{2}$ endast används i den nedre raden av utdata, så det krävs bara att den är $99$ rader hög; och därför behöver den vänstra faktorn $A_{21}+A_{22}$ som används för att generera den bara vara $99$ rader hög; följaktligen finns det inget behov av att fylla den summan till $100$ rader; det är bara nödvändigt att fylla $A_{22}$ till $100$ kolumner för att matcha $A_{21}$ .

Vidare finns det inget behov av att matriserna är kvadratiska. Icke-kvadratiska matriser kan delas på mitten med samma metoder, vilket ger mindre icke-kvadratiska matriser. Om matriserna är tillräckligt icke-kvadratiska kommer det att vara värt besväret att reducera den initiala operationen till fler kvadratiska produkter, med enkla metoder som i huvudsak är ${\displaystyle O(n^{2})} ,$ till exempel:

• En produkt med storleken $[2N\ gånger N]\ast [N\ gånger 10N]$ kan göras som 20 separata $[N\ gånger N]\ast [N\ gånger N]$ operationer, arrangerade för att bilda resultatet;
• En produkt med storleken $[N\times 10N]\ast [10N\times N]$ kan göras som 10 separata $[N\ gånger N]\ast [N\ gånger N]$ operationer, summerade för att bilda resultatet.

Dessa tekniker kommer att göra implementeringen mer komplicerad, jämfört med att bara utfylla till en tvåkraftsruta; Det är dock ett rimligt antagande att alla som genomför en implementering av Strassen, snarare än konventionell multiplikation, kommer att prioritera beräkningseffektivitet högre än på enkelheten i implementeringen.

I praktiken kan Strassens algoritm implementeras för att uppnå bättre prestanda än konventionell multiplikation även för små matriser, för matriser som inte alls är kvadratiska och utan att kräva arbetsyta bortom buffertar som redan behövs för en högpresterande konventionell multiplikation.

Se även

• Beräkningskomplexitet av matematiska operationer
• Eliminering av Gauss–Jordan
• Coppersmith–Winograd-algoritm
• Z-ordnings matrisrepresentation
• Karatsuba-algoritm $) {\displaystyle O(n ^{2})}$ för att multiplicera n -siffriga heltal i $O(n^{\log _{2}3})$ istället för i tid
• Toom-Cook-algoritmen , en snabbare generalisering av Karatsuba-algoritmen som tillåter rekursiv dela-och-härska-nedbrytning i mer än 2 block åt gången
• Gauss komplexa multiplikationsalgoritm multiplicerar två komplexa tal med 3 reella multiplikationer istället för 4

•   Thomas H. Cormen , Charles E. Leiserson , Ronald L. Rivest och Clifford Stein . Introduktion till algoritmer, andra upplagan. MIT Press och McGraw-Hill, 2001. ISBN 0-262-03293-7 . Kapitel 28: Avsnitt 28.2: Strassens algoritm för matrismultiplikation, s. 735–741.
•   Knuth, Donald (1997). Konsten att programmera, seminumeriska algoritmer . Vol. II (3:e upplagan). Addison-Wesley. ISBN 0-201-89684-2 .

externa länkar

• Weisstein, Eric W. "Strassens formler" . MathWorld . (Innehåller även formler för snabb matrisinversion )
• Tyler J. Earnest, Strassens algoritm för mobilbredbandsmotorn