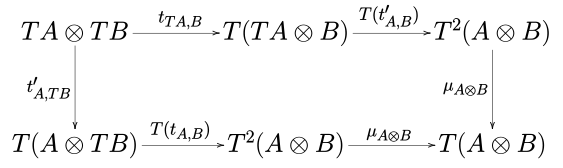Stark monad

I kategoriteorin är en stark monad över en monoidal kategori ( C , ⊗, I) en monad ( T , η, μ) tillsammans med en naturlig transformation t _A,B : A ⊗ TB → T ( A ⊗ B ), kallad ( tensorial ) styrka , så att diagrammen

, ,

, och

pendla för varje objekt A , B och C (se definition 3.2 i ).

Om den monoida kategorin ( C , ⊗, I) är sluten är en stark monad samma sak som en C -berikad monad.

Kommutativa starka monader

För varje stark monad T på en symmetrisk monoidal kategori kan en naturlig transformation med medstyrka definieras av

$t'_{A,B}=T( \gamma _{B,A})\circ t_{B,A}\circ \gamma _{TA,B}:TA\otimes B\to T(A\otimes B)$ .

En stark monad T sägs vara kommutativ när diagrammet

pendlar för alla objekt $A$ och $B$ .

Ett intressant faktum om kommutativa starka monader är att de är "samma som" symmetriska monoidala monader . Mer uttryckligen,

• en kommutativ stark monad $(T,\eta ,\mu ,t)$ definierar en symmetrisk monoidal monad $(T,\eta) ,\mu ,m)$ m

$\displaystyle m_{A, B}=\mu _{A\otimes B}\circ Tt'_{A,B}\circ t_{TA,B}:TA\otimes TB\to T(A\otimes B)} och omvänt en symmetrisk$

• monoidal monad $(T,\eta ,\mu ,m)$ definierar en kommutativ stark monad $(T,\eta ,\mu ,t)$ av

$t_{A,B}=m_{A,B }\circ (\eta _{A}\otimes 1_{TB}):A\otimes TB\to T(A\otimes B)$

och omvandlingen mellan den ena och den andra presentationen är bijektiv.

•   Anders Kock (1972). "Starka funktorer och monoida monader" (PDF) . Archiv der Mathematik . 23 : 113–120. doi : 10.1007/BF01304852 . S2CID 13246783 .
•   Jean Goubault-Larrecq, Slawomir Lasota och David Nowak (2005). "Logiska relationer för monadiska typer". Matematiska strukturer i datavetenskap . 18 (6): 1169. arXiv : cs/0511006 . doi : 10.1017/S0960129508007172 . S2CID 741758 .