Stagnationspunktsflöde

I vätskedynamik representerar stagnationspunktsflöde flödet av en vätska i omedelbar närhet av en stagnationspunkt (eller en stagnationslinje) med vilken stagnationspunkten (eller linjen) identifieras för ett potentiellt flöde eller inviscid flöde . Flödet beaktar specifikt en klass av stagnationspunkter som kallas sadelpunkter där de inkommande strömlinjerna avleds och riktas utåt i en annan riktning; strömlinjeavböjningarna styrs av separatriser. Flödet i närheten av stagnationspunkten eller linjen kan generellt beskrivas med hjälp av potentiell flödesteori , även om viskösa effekter inte kan försummas om stagnationspunkten ligger på en fast yta.

Stagnationspunktsflöde utan fasta ytor

När två strömmar av antingen tvådimensionell eller axisymmetrisk natur träffar varandra ortogonalt, skapas ett stagnationsplan, där de inkommande strömmarna avleds tangentiellt utåt; på stagnationsplanet är således hastighetskomponenten vinkelrät mot det planet noll, medan den tangentiella komponenten är icke-noll. I närheten av stagnationspunkten kan en lokal beskrivning av hastighetsfältet beskrivas.

Allmänt tredimensionellt hastighetsfält

Stagnationspunktsflödet motsvarar ett linjärt beroende av koordinaterna, som kan beskrivas i de kartesiska koordinaterna $(x,y,z)$ med hastighetskomponenter $(v_{x},v_{y},v_{z})$ enligt följande

v_{x}=\alpha x,\quad v_{y}=\beta y,\quad v_{z}=\gamma z

där $(\alpha ,\beta ,\gamma )$ är konstanter som kallas töjningshastigheterna; dessa konstanter är inte helt godtyckliga eftersom kontinuitetsekvationen kräver ${\displaystyle \alpha +\beta +\gamma =0} ,$ det vill säga bara två av de tre konstanterna är oberoende. Vi ska anta $\gamma <0\leq \alpha$ så att flödet är mot stagnationspunkten i $z$ -riktningen och bort från stagnationspunkten i $x$ riktning. Utan förlust av generalitet kan man anta att $\beta \geq \alpha$ . Flödesfältet kan kategoriseras i olika typer baserat på en enda parameter

\lambda ={\frac {\alpha -\beta }{\alpha +\beta }}

Plana stagnationspunktsflöde

Det tvådimensionella stagnationspunktsflödet tillhör fallet $\beta =0\,(\lambda =1)$ . Flödesfältet beskrivs enligt följande

v_{x}=kx,\quad v_{z}=-kz

där vi låter $k=\alpha =-\gamma >0$ . Detta flödesfält undersöks så tidigt som 1934 av GI Taylor . I laboratoriet skapas detta flödesfält med hjälp av en apparat med fyra kvarnar, även om dessa flödesfält är allestädes närvarande i turbulenta flöden.

Axisymmetriskt stagnationspunktsflöde

Det axisymmetriska stagnationspunktsflödet motsvarar $\alpha =\beta \,(\lambda =0)$ . Flödesfältet kan enkelt beskrivas i cylindriskt koordinatsystem $(r,\theta ,z)$ med hastighetskomponenter $(v_{r}, 0,v_{z})$ enligt följande

v_{r}=kr,\quad v_{z}=-2kz

där vi låter $k=\alpha =\beta =-\gamma /2>0$ .

Radiella stagnationsflöden

I radiella stagnationsflöden har vi istället för en stagnationspunkt en stagnationscirkel och stagnationsplanet ersätts av en stagnationscylinder. Det radiella stagnationsflödet beskrivs med hjälp av det cylindriska koordinatsystemet $(r,z)$ med hastighetskomponenter $(v_{r},v_{z})$ som följer

v_{r}=-k\left(r-{\frac {r_{s}^{2}}{r }}\right),\quad v_{z}=2kz

där $r_{s}$ är platsen för stagnationscylindern.

Hiemenz flöde

Tvådimensionellt stagnationspunktsflöde

Flödet på grund av närvaron av en fast yta vid $z=0$ i plant stagnationspunktflöde beskrevs först av Karl Hiemenz 1911, vars numeriska beräkningar för lösningarna förbättrades senare av Leslie Howarth . Ett välbekant exempel där Hiemenz-flöde är tillämpbart är den framåtgående stagnationslinjen som uppstår i flödet över en cirkulär cylinder.

Den fasta ytan ligger på $xy$ . Enligt potentiell flödesteori beskrivs vätskerörelsen i termer av strömfunktionen $\psi$ och hastighetskomponenterna $(v_{x},0,v_{z} )$ ges av

\psi =kxz,\quad v_{x}=kx,\quad v_{z}=-kz.

Stagnationslinjen för detta flöde är $(x,y,z)=(0,y,0)$ . Hastighetskomponenten $v_{x}$ är icke-noll på den fasta ytan, vilket indikerar att ovanstående hastighetsfält inte uppfyller halkfria gränsvillkor på väggen. För att hitta de hastighetskomponenter som uppfyller det halkfria gränsvillkoret antar man följande form

\psi ={\sqrt {\nu k}}xF(\eta ),\quad \eta ={\frac {z}{\ sqrt {\nu /k}}}

där $\nu$ är den kinematiska viskositeten och ${\sqrt {\nu /k}}$ är den karakteristiska tjockleken där viskösa effekter är signifikanta. Förekomsten av konstant värde för den viskösa effektens tjocklek beror på den konkurrerande balansen mellan vätskekonvektionen som är riktad mot den fasta ytan och viskös diffusion som är riktad bort från ytan. Således kan virveln som produceras vid den fasta ytan diffundera endast till avstånd av ordningen ${\sqrt {\nu /k}}$ ; analoga situationer som liknar detta beteende förekommer i asymptotisk sugprofil och von Kármán virvlande flöde . Hastighetskomponenterna, trycket och Navier–Stokes ekvationer blir då

v_{x}=kxF' ,\quad v_{z}=-{\sqrt {\nu k}}F,\quad {\frac {p_{o}-p}{\rho }}={\frac {1}{2}}k ^{2}x^{2}+k\nu F'+{\frac {1}{2}}k\nu F^{2}

{\ displaystyle F'''+FF''-F'^{2}+1=0}

Kraven på att $(v_{x},v_{z})=(0,0)$ vid $z=0$ och att $v_{x}\rightarrow kx$ som $z\rightarrow \infty$ översätt till

F(0)=0,\ F'(0)=0,F'(\infty )=1.

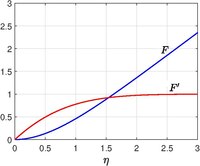
Villkoret för $v_{z}$ som $z\rightarrow \infty$ kan inte föreskrivas och erhålls som en del av lösningen. Problemet som formuleras här är ett specialfall av Falkner-Skan gränsskikt . Lösningen kan erhållas från numeriska integrationer och visas i figuren. De asymptotiska beteendena för stora $\eta \rightarrow \infty$ är

F\sim \eta -0,6479,\quad v_{x,} \quad v_{z}\sim -k(z-\delta ^{*}),\quad \delta ^{*}=0,6479\delta

där $\delta ^{*}$ är förskjutningstjockleken .

Stagnationspunktsflöde med en översättande vägg

Hiemenz flöde när den solida väggen översätts med en konstant hastighet $U$ längs $x$ löstes av Rott (1956). Detta problem beskriver flödet i närheten av den främre stagnationslinjen som uppträder i ett flöde över en roterande cylinder. Den erforderliga streamfunktionen är

\psi ={\sqrt {\nu k}}xF(\eta )+U\delta \int _{0} ^{\eta }G(\eta )d\eta

där funktionen $G(\eta )$ uppfyller

G''+FG'-F'G=0,\quad G(0)=1,\quad G(\infty )=0

Lösningen till ovanstående ekvation ges av $G(\eta )=F''(\eta )/F''(0).$

Sned stagnationspunktsflöde

Om den inkommande strömmen är vinkelrät mot stagnationslinjen, men närmar sig snett, är det yttre flödet inte potentiellt, utan har en konstant virvel $-\zeta _{o}$ . Lämplig strömfunktion för sned stagnationspunktsflöde ges av

\psi =kxz+{\frac {1}{2}}\zeta _{o}z^{2}

Viskösa effekter på grund av närvaron av en solid vägg studerades av Stuart (1959), Tamada (1979) och Dorrepaal (1986). I deras tillvägagångssätt tar streamfunktionen formen

\psi ={\sqrt {\nu k}}xF(\eta )+\zeta _{o}\ delta ^{2}\int _{0}^{\eta }H(\eta )d\eta

där funktionen $H(\eta )$

H''+FH'-F'H=0,\quad H(0)=0,\ quad H'(\infty )=1

.

Homann flöde

Homann flöde med injektion

Homann flöde med sug

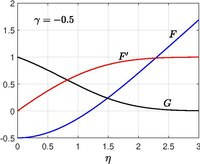
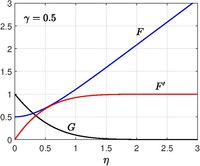
Lösningen för axisymmetriskt stagnationspunktflöde i närvaro av en solid vägg erhölls först av Homann (1936). Ett typiskt exempel på detta flöde är den främre stagnationspunkten som uppträder i ett flöde förbi en sfär. Paul A. Libby (1974)(1976) utökade Homanns arbete genom att tillåta den solida väggen att förflytta sig längs sitt eget plan med en konstant hastighet och tillåta konstant sug eller injektion vid den fasta ytan.

Lösningen på detta problem erhålls i det cylindriska koordinatsystemet $(r,\theta ,z)$ genom att införa

\eta ={\frac {z}{\sqrt {\nu /k}}},\quad \gamma =-{\frac {V}{2{\sqrt {k\nu }}}},\quad v_{r}=krF'(\eta )+U\cos \theta G(\eta ),\quad v_{\theta }=-U\sin \theta G( \eta ),\quad v_{z}=-2{\sqrt {k\nu }}F(\eta )

där $U$ är väggens translationshastighet och $V$ är insprutningshastigheten (eller sughastigheten vid väggen). Problemet är endast axelsymmetriskt när $U=0$ . Trycket ges av

{\frac {p-p_{o}}{\rho }}=-{\frac {1 }{2}}k^{2}r^{2}-2k\nu (F^{2}+F')

Navier –Stokes ekvationer reduceras sedan till

{\begin{aligned}F'''+2FF''-F'^{2 }+1&=0,\\G''+2FG'-F'G&=0\end{aligned}}

tillsammans med randvillkor,

F(0)=\gamma ,\quad F'(0 )=0,\quad F'(\infty )=1,\quad G(0)=1,\quad G(\infty )=0.

När $U=V=0$ återställs det klassiska Homann-problemet.

Plan motströmmar

Jets som kommer ut från en slot-jets skapar stagnationspunkt däremellan enligt potentiell teori. Flödet nära stagnationspunkten kan studeras med hjälp av självliknande lösning. Denna inställning används ofta i förbränningsexperiment . Den första studien av infallande stagnationsflöden beror på CY Wang. Låt två vätskor med konstanta egenskaper betecknade med suffix $1({\text{top}}),\ 2({\text{bottom}})$ strömmande från motsatt riktning, träffa, och anta att de två vätskorna är oblandbara och att gränssnittet (beläget vid $y=0$ ) är plant. Hastigheten ges av

u_{1}=k_{1}x,\quad v_{1}= -k_{1}y,\quad u_{2}=k_{2}x,\quad v_{2}=-k_{2}y

där $k_{1},\ k_{2}$ är töjningshastigheter för vätskorna. Vid gränsytan måste hastigheter, tangentiell spänning och tryck vara kontinuerliga. Vi introducerar den självliknande transformationen,

\eta _{1}={\sqrt {\frac {\nu _{ 1}}{k_{1}}}}y,\quad u_{1}=k_{1}xF_{1}',\quad v_{1}=-{\sqrt {\nu _{1}k_{ 1}}}F_{1}

\eta _{2}={\ sqrt {\frac {\nu _{2}}{k_{2}}}}y,\quad u_{2}=k_{2}xF_{2}',\quad v_{2}=-{\sqrt {\nu _{2}k_{2}}}F_{2}

resultatekvationer,

F_{1}'''+F_{1}F_{1}''-F_{1}'^{2}+1=0,\quad {\frac {p_{o1}-p_ {1}}{\rho _{1}}}={\frac {1}{2}}k_{1}^{2}x^{2}+k_{1}\nu _{1}F_{ 1}'+{\frac {1}{2}}k_{1}\nu _{1}F_{1}^{2}

F_{2}'''+F_{2}F_{2}''-F_{2}'^{2}+1=0,\quad {\frac {p_{o2}-p_{2 }}{\rho _{2}}}={\frac {1}{2}}k_{2}^{2}x^{2}+k_{2}\nu _{2}F_{2} '+{\frac {1}{2}}k_{2}\nu _{2}F_{2}^{2}.

Tillståndet utan penetration vid gränssnittet och fritt strömtillstånd långt borta från stagnationsplanet blir

F_{1}(0)=0,\quad F_{1} '(\infty )=1,\quad F_{2}(0)=0,\quad F_{2}'(-\infty )=1.

Men ekvationerna kräver ytterligare två randvillkor. Vid $\eta =0$ , tangentialhastigheterna $u_{1}=u_{2}$ , tangentialspänningen $\rho _{1}\nu _{1}\partial u_{1}/\partial y=\rho _{2}\nu _{2}\partial u_{ 2}/\partial y$ och trycket $p_{1}=p_{2}$ är kontinuerliga. Därför,

{\begin{aligned}k_{1}F_{1}'(0)&=k_{2}F_{2}'(0),\\\rho _{1}{\sqrt {\nu _{1}k_{1}^{3}}}F_{1}''(0)&=\rho _{2}{\sqrt {\nu _{2}k_{2}^{3}} }F_{2}''(0),\\p_{o1}-\rho _{1}\nu _{1}k_{1}F_{1}'(0)&=p_{o2}-\ rho _{2}\nu _{2}k_{2}F_{2}'(0).\end{aligned}}

där $\rho _{1}k_{1}^{2}=\rho _{2}k_{2}^{2}$ (från yttre inviscid problem ) är använd. Både $F_{i}'(0),F_{i}''(0)$ är inte kända apriori , men härledda från matchande villkor. Den tredje ekvationen är att bestämma variationen av yttre tryck $p_{o1}-p_{o2}$ på grund av effekten av viskositet. Så det finns bara två parametrar, som styr flödet, vilka är